Federated Reconnaissance: Efficient, Distributed, Class-Incremental Learning 论文阅读+代码解析
论文地址点这里
一. 介绍
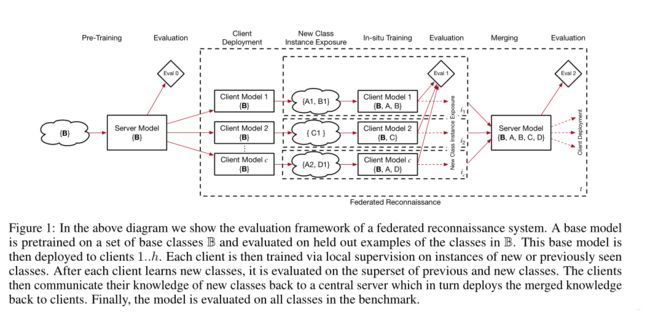
论文中,作者提出了联合侦察,这是一类新的学习问题,分布式模型应该能够独立地学习新的概念,并有效地共享这些知识。通常在联合学习中,单个静态类集由每个客户端学习。相反,联邦侦察要求每个客户机可以单独学习一组不断增长的类,并与其他客户机有效地交流之前观察到的和新的类的知识。这种关于学习类的交流可以从客户那里获得知识;然后期望最终合并的模型支持每个客户机已公开的类的超集。然后可以将合并的模型部署回客户端进行进一步的学习。
1.1 早期的工作
持续学习: 不断学习新概念是一个开放的和长期的问题在机器学习和人工智能没有表面上的一个统一的解决方案。虽然深度神经网络已被证明在广泛的任务中是非常有效的,但持续整合新信息的可用方法,同时记住以前学到的概念会变得效率低下。在这项工作中,我们假设访问一组训练前的数据,并探索算法,允许高效和准确的学习新类的顺序。
联邦学习: 与持续学习不同,联邦学习再中央服务器的指导下,对分散的设备上的数据迭代地训练一个公共模型(目前也有基于个性化的以适应各个客户)。之前我写的一篇博客,介绍了联邦持续学习模型,和本篇文章背景类似。但本篇文章注重到类知识的直接共享
1.2 贡献
一个有效的联邦侦查系统必须解决新类的高效学习与知识的保存转移。因此,作者将普通的随机梯度下降作为下界,iCaRL算法用于联邦侦查的比较以及将所有客户的所有训练数据联合分布的SGD作为上界。
假设,当一个预训练的数据集可用时,原型网络时一个强大的基线(原型网路之后我会再写一个博客),原因为:
它能够将概念压缩成相对较小的载体,即所谓的原型,从而实现高效的通信
在非iid数据上学习时,对灾难性遗忘的鲁棒性
在模型合并过程中,不需要基于梯度的学习或超参数调优,从而实现快速的知识转移。
作者提出了Federated prototypical network架构,对类增量进行学习。
二. 联邦侦查问题陈述
2.1 系统需求
联邦侦察需要对每个客户端设备进行持续的学习、高效的通信和知识合并。受到在大量分布式客户端设备上学习新类的应用程序的启发,我们定义了联邦侦察学习系统的以下需求:
- 每个客户端模型应该能够从几个示例中就地学习新的类,并且能够随着更多示例的出现而提高准确性。
- 在学习了新的类之后,每个模型都不应该忘记之前看过的类。也就是说,模型不应该遭受灾难性的遗忘。
- 为了降低通信成本,并在带宽有限的情况下实现分布式学习,联邦侦察系统应该能够在传输前压缩信息。
- 最后,为了避免每次客户机遇到新类时对中央服务器上的所有数据进行昂贵的重新训练,联邦侦察系统应该能够快速合并分布式客户机模型学习到的新类的知识。
联邦侦察的实际实现的具体要求当然将决定每个需求的细节和相对重要性。
2.2 问题定义
联邦侦查由一组客户端组成 C : = { c i ∣ i ∈ 1... C } \mathbb{C}:=\{c_i|i\in 1...C\} C:={ci∣i∈1...C},每一个客户端都经历着类不断增加的情况 M i , t : = { p ( y = j ∣ x ) ∣ j ∈ 1... M j } \mathbb{M}_{i,t}:=\{p(y=j|x)|j\in 1...M_j\} Mi,t:={p(y=j∣x)∣j∈1...Mj}。其中 C C C表示客户端的总数, M i M_i Mi则表示一个客户端能区分的类的总数,一个类由概率 p ( y = j ∣ x ) p(y=j|x) p(y=j∣x)通过标签j和x进行表示。中央服务器的工作是合并客户机关于类的知识 M t = ⋃ i = 1 C M i , t \mathbb{M}_t=\bigcup^C_{i=1}\mathbb{M}_{i,t} Mt=⋃i=1CMi,t然后部署更新的模型并将模型 M t \mathbb{M}_t Mt返回给 C \mathbb{C} C。一个客户端 C i C_i Ci可以通过直接使用一组标记的例子进行训练从而接触到一个新的类 { ( x , y ) ∣ ( x , y ) ∈ X j × Y j } \{(x,y)|(x,y)\in X_j \times Y_j\} {(x,y)∣(x,y)∈Xj×Yj},或者交换经过压缩的知识,使得客户端近似估计 p ( y = j ∣ x ) p(y=j|x) p(y=j∣x)。
一个有效的联邦侦查系统需要有效的评估我们的预测值 p ( y ^ = j ∣ x ) p(\hat{y}=j|x) p(y^=j∣x)无论是否是直接学习样本j或者从别的客户端获得知识。因此我们联邦侦查学习系统在任何时间的分布式目标函数即为客户端的平均损失:
L = 1 C ∑ i = 1 C 1 J i ∑ j = 1 J i 1 K i , j ∑ k = 1 K i , j H ( y ^ i , j , k , y i , j , k ) (1) \mathcal{L}=\frac{1}{\mathbb{C}}\sum^{\mathbb{C}}_{i=1}\frac{1}{J_i}\sum^{J_i}_{j=1}\frac{1}{K_{i,j}}\sum^{K_{i,j}}_{k=1}H(\hat{y}_{i,j,k},y_{i,j,k}) \tag 1 L=C1i=1∑CJi1j=1∑JiKi,j1k=1∑Ki,jH(y^i,j,k,yi,j,k)(1)
其中 J i J_i Ji表示客户端i已经遇到过的所有类的总数, K i , j K_{i,j} Ki,j表示客户端i上第j个类的例子数,H为交叉熵损失对我们的预测值和真实值进行计算。为了简便计算,假设在整个部署过程中客户端数量是固定的,尽管随着时间的推移扩展到可变数量的客户端是很简单的。
在每一时刻t,一个很少例子的数据集 D t D_t Dt随着环境而诞生。联邦侦查面对着两个问题:客户端从头开始学习知识 p ( X , Y ) p(X,Y) p(X,Y)以及基类 B \mathbb{B} B的子集用于预训练。集合 B \mathbb{B} B类似元学习中的元训练集,我们希望客户学习越来越多的超集的类包括基础类和领域类中那些在预训练之后的 B \mathbb{B} B。在实践中,访问表示 B \mathbb{B} B的数据集是一个合理的假设,因为在部署联邦侦查系统之前,通常可以测量一些训练前类的数量。
模型合并之后,我们通过获取类的期望来定义预期损失:
L t = 1 ∣ M t ∣ ∑ j = 1 ∣ M t ∣ 1 K i , j ∑ k = 1 K i , j H ( y ^ i , j , k , y i , j , k ) (2) \mathcal{L}_t=\frac{1}{|\mathbb{M}_t|}\sum^{|\mathbb{M}_t|}_{j=1}\frac{1}{K_{i,j}}\sum^{K_{i,j}}_{k=1}H(\hat{y}_{i,j,k},y_{i,j,k}) \tag 2 Lt=∣Mt∣1j=1∑∣Mt∣Ki,j1k=1∑Ki,jH(y^i,j,k,yi,j,k)(2)
准确率为:
L t = 1 ∣ M t ∣ ∑ j = 1 ∣ M t ∣ 1 K i , j ∑ k = 1 K i , j [ y ^ i , j , k = y i , j , k ] (3) \mathcal{L}_t=\frac{1}{|\mathbb{M}_t|}\sum^{|\mathbb{M}_t|}_{j=1}\frac{1}{K_{i,j}}\sum^{K_{i,j}}_{k=1}[\hat{y}_{i,j,k}=y_{i,j,k}] \tag 3 Lt=∣Mt∣1j=1∑∣Mt∣Ki,j1k=1∑Ki,j[y^i,j,k=yi,j,k](3)
在每个时刻t,每个客户端模型首先呈现一些标记的新类数据,然后针对这个新的类的超级和它在历史中所有类的数据进行评估。在本地训练完之后,客户端将信息发送会服务端,选择通信新的类信息或者更新之前看到的类的信息,服务器将多个客户端的信息合并在一起。这个模型评估之后,我们评估集类和领域类的准确率。客户端学习和交流知识的过程在服务器重复迭代。因此,我们需要最小化方程(1)在任务 { t ∈ N ∣ t ≤ T } \{t \in \mathbb{N}|t\le T\} {t∈N∣t≤T}:
min t ∈ 1 , . . . T E [ L t ] (4) \min_{t\in 1,...T}\mathbb{E}[\mathcal{L_t}] \tag 4 t∈1,...TminE[Lt](4)
或者,当学习完固定数量的任务之后:
min L t = T (5) \min \mathcal{L}_{t=T} \tag{5} minLt=T(5)
为了简单,突出分布式学习的挑战,作者根据(5)进行评估。
三. 方法
3.1 学习的算法
(这里作者说了自己比较了哪些方法,由于本博客主要是学习思想,因此就不写了)
3.2 联邦原型网络(Federated Prototypical Networks)
我们提出使用原型网络来有效地循序学习新类。由于原型网络在测试时不是基于梯度的,因此在学习新类时,通过对足够多的类进行判别性预训练,可以使它们对灾难性遗忘具有鲁棒性。当在联邦侦察基准上进行评估时,我们可以通过简单地存储之前的原型(方差)和用于计算之前原型的示例数量来计算每个类的均值(如果需要的话,还有方差)的无偏估计。我们根据定义了原型网络:
z = f θ ( x i ) (6) z = f_\theta(x_i) \tag 6 z=fθ(xi)(6)
z ˉ j = 1 ∣ S j ∣ ∑ ( x i , y i ) ∈ S j f θ ( x i ) (7) \bar{z}_j=\frac{1}{|S_j|}\sum_{(x_i,y_i)\in S_j}f_\theta(x_i) \tag 7 zˉj=∣Sj∣1(xi,yi)∈Sj∑fθ(xi)(7)
其中 f f f为一个由 θ \theta θ和 S j S_j Sj参数化的神经嵌入网络( S j S_j Sj表示为支持集)。一个原型网络的训练是在查询示例上最小化交叉熵损失,其中预测类被视为查询嵌入和支持数据原型之间的负欧氏距离的softmax:
p θ ( y = j ∣ x ) = e x p ( − d ( f θ ( x ) , z ˉ j ) ) ∑ j ′ ∈ J e x p ( − d ( f θ ( x ) , z ˉ j ′ ) ) (8) p_\theta(y=j|x)=\frac{exp(-d(f_\theta(x),\bar{z}_j))}{\sum_{j'\in J}exp(-d(f_\theta(x),\bar{z}_{j'}))} \tag 8 pθ(y=j∣x)=∑j′∈Jexp(−d(fθ(x),zˉj′))exp(−d(fθ(x),zˉj))(8)
现在,我们希望能够为多个客户端在当前时间步中观察到的或在之前的历史中观察到的类的原型计算出无偏的估计。为了提高存储和通信的效率,我们可以通过存储之前的原型和用于计算它的示例数量,来为每个原型计算一个无偏的运行平均值,而不是存储一个类的所有原始示例或甚至是所有示例嵌入:
μ t = k t − 1 μ t − 1 k t + ( k t − k t − 1 ) z ˉ j k t (9) \mu_t = \frac{k_{t-1}\mu_{t-1}}{k_t}+\frac{(k_t-k_{t-1})\bar{z}_j}{k_t} \tag 9 μt=ktkt−1μt−1+kt(kt−kt−1)zˉj(9)
其中 k t k_t kt是在时间t上观察到类j的数量, μ t \mu_t μt为对类j上所有例子的 z z z的平均值。最后根据大叔定理,可以求出 μ ∗ \mu^* μ∗:
z ˉ k → a . s . μ ∗ a s k → ∞ (10) \bar z_k \xrightarrow{a.s.} \mu^*\ \ \ \ as\ k\rightarrow \infty \tag {10} zˉka.s.μ∗ as k→∞(10)
在实际问题中,相关的数值不能被忽视,因此采用一种更稳定的方法来计算:
μ t ← μ t − 1 + k t − k t − 1 k t ( z ˉ − μ t − 1 ) (11) \mu_t \leftarrow \mu_{t-1}+\frac{k_t-k_{t-1}}{k_t}(\bar z - \mu_{t-1}) \tag{11} μt←μt−1+ktkt−kt−1(zˉ−μt−1)(11)
具体的算法如下图:

四.关键代码解读
代码地址点这里
总的来说,本篇论文还是基于prototypical network来进行的,如果对prototypical network有疑问的也可以看看代码,代码比较简单。
4.1 元训练部分
首先就是我们需要定义prototypical网络,也就是计算出z来。
class PrototypicalNetwork(nn.Module):
def __init__(
self,
in_channels,
out_channels,
hidden_size=64,
pooling: Optional[str] = None,
backbone: str = "4conv",
l2_normalize_embeddings: bool = False,
drop_rate: Optional[float] = None,
):
"""Standard prototypical network"""
super().__init__()
self.supported_backbones = {"4conv", "resnet18"}
assert backbone in self.supported_backbones
self.pooling = pooling
self.backbone = backbone
self.in_channels = in_channels
self.out_channels = out_channels
self.hidden_size = hidden_size
## 网络层,这里用的是4conv也就是4个卷机层
if self.backbone == "resnet18":
self.encoder = build_resnet18_encoder(drop_rate=drop_rate)
elif self.backbone == "4conv":
self.encoder = build_4conv_protonet_encoder(
in_channels, hidden_size, out_channels, drop_rate=drop_rate
)
else:
raise ValueError(
f"Unsupported backbone {self.backbone} not in {self.supported_backbones}"
)
if self.pooling is not None:
assert self.pooling in SUPPORTED_POOLING_LAYERS
if self.pooling == "Gem":
self.gem_pooling = GeM()
else:
self.gem_pooling = None
self.l2_normalize_embeddings = l2_normalize_embeddings
def forward(self, inputs):
batch, nk, _, _, _ = inputs.shape
inputs_reshaped = inputs.view(
-1, *inputs.shape[2:]
) # -> [b * k * n, input_ch, rows, cols]
embeddings = self.encoder(
inputs_reshaped
) # -> [b * n * k, embedding_ch, rows, cols]
# TODO: add optional support for half for further prototype/embedding compression
# embeddings = embeddings.type(torch.float16)
# RuntimeError: "clamp_min_cpu" not implemented for 'Half'
if self.pooling is None:
embeddings_reshaped = embeddings.view(
*inputs.shape[:2], -1
) # -> [b, n * k, embedding_ch * rows * cols] (4608 for resnet 18)
elif self.pooling == "average":
embeddings_reshaped = embeddings.mean(dim=[-1, -2]).reshape(
batch, nk, -1
) # -> [b, n * k, embedding_ch] (512 for resnet 18)
elif self.pooling == "Gem":
embeddings_reshaped = (
self.gem_pooling(embeddings).squeeze(-1).squeeze(-1).unsqueeze(0)
)
else:
raise ValueError
if self.l2_normalize_embeddings:
embeddings_reshaped = torch.nn.functional.normalize(
embeddings_reshaped, p=2, dim=2
)
return embeddings_reshaped
看着很复杂,其实就是4个卷积层构成的,作者这里的hidden_size为64(64个3*3的卷积核),因此假如说一个batch的x为[1,25,1,28,28](类似于元学习,第一个1表示有一个任务,25表示一个任务包含的数据量,这里是5way5shot所以是25,第三个1表示通道,之后为图片),经过encorder之后变为:[25,64,1,1],之后变了一下形状变为encorder = [1,25,64]方便之后计算。
我们看计算z:
z ˉ j = 1 ∣ S j ∣ ∑ ( x i , y i ) ∈ S j f θ ( x i ) \bar{z}_j=\frac{1}{|S_j|}\sum_{(x_i,y_i)\in S_j}f_\theta(x_i) zˉj=∣Sj∣1(xi,yi)∈Sj∑fθ(xi)
也就是对一个类的样本算平均,代码如下:
def get_prototypes(
embeddings,
n_classes,
k_shots_per_class,
return_sd: bool = False,
prototype_normal_std_noise: Optional[float] = None,
):
batch_size, embedding_size = embeddings.size(0), embeddings.size(-1)
embeddings_reshaped = embeddings.reshape(
[batch_size, n_classes, k_shots_per_class, embedding_size]
)
prototypes = embeddings_reshaped.mean(2)
# print(f"Prototype shape for {n_classes} [batch, n_classes, embedding_size]: {prototypes.shape}")
assert len(prototypes.shape) == 3
if prototype_normal_std_noise is not None:
prototypes += torch.normal(
torch.zeros_like(prototypes),
torch.ones_like(prototypes) * prototype_normal_std_noise,
)
if return_sd:
return prototypes, embeddings_reshaped.std(2)
return prototypes
首先对我们的5way5shot拆分encorder,变为[1,5,5,64],之后对我们的每一个类中的样本求平均(也就是5个example进行平均),算出来的z就为:[1,5,64]
然后最后就是计算loss:
p θ ( y = j ∣ x ) = e x p ( − d ( f θ ( x ) , z ˉ j ) ) ∑ j ′ ∈ J e x p ( − d ( f θ ( x ) , z ˉ j ′ ) ) p_\theta(y=j|x)=\frac{exp(-d(f_\theta(x),\bar{z}_j))}{\sum_{j'\in J}exp(-d(f_\theta(x),\bar{z}_{j'}))} pθ(y=j∣x)=∑j′∈Jexp(−d(fθ(x),zˉj′))exp(−d(fθ(x),zˉj))
对我们的query set也进行encorder然后和我们的z计算softmax,对应代码如下:
def prototypical_loss(
prototypes, embeddings, targets, sum_loss_over_examples, **kwargs
):
## 求距离d
squared_distances = torch.sum(
(prototypes.unsqueeze(2) - embeddings.unsqueeze(1)) ** 2, dim=-1
)
if sum_loss_over_examples:
reduction = "sum"
else:
reduction = "mean"
## \frac{exp(-d(f_\theta(x),\bar{z}_j))}{\sum_{j'\in J}exp(-d(f_\theta(x),\bar{z}_{j'}))}
return F.cross_entropy(-squared_distances, targets, reduction=reduction, **kwargs)
不断迭代更新出我们的encorder层中的参数即可。
4.2 元测试部分——类增量
再完成训练后,我们的enocrder参数达到最佳 θ ∗ \theta^* θ∗,此时我们来进行元测试,进行类增量的测试。
首先是网络层和元训练一样,直接加载我们的参数即可。由于是类增量,我们需要一个一个类的进行增加。同理,对一个类的数据拆为train set和test set,这里train中每个类包含15个样本,test则为5个。假设当前由n个类,首先从train set(只计算当前类)计算encorder 由[1,15,1,28,28]变为[1,15,64],之后计算prototype变为[1,64],再加上之前存储的前几个类的prototype变为:[1,n,64]。test set也经过encorder变为[1,5*n,64]。
train_embeddings = self.forward(train_inputs)
test_embeddings = self.forward(test_inputs)
## 计算z
all_class_prototypes = self._get_prototypes(
train_embeddings, train_labels, n_train_classes, k_shots
)
计算z,由于只有当前类的信息,因此我们需要存储之前出现类的z,然后一起concat即可。
def _get_prototypes(
self,
train_embeddings: torch.Tensor,
train_labels: torch.Tensor,
n_train_classes: int,
k_shots: int,
):
new_prototypes = get_prototypes(
train_embeddings, n_train_classes, k_shots
) # -> [b, n, features]
# Add each prototype to the model:
assert len(new_prototypes.shape) == 3
assert new_prototypes.shape[0] == 1
new_prototypes = new_prototypes[
0
] # Assume single element in batch dimension. Now [n_train_classes, features]
class_indices = train_labels.unique()
for i, cls_index in enumerate(class_indices):
self.update_prototype_for_class(
cls_index, new_prototypes[i, :], train_labels.shape[1]
)
all_class_prototypes = [
self.prototypes[key] for key in sorted(self.prototypes.keys())
]
all_class_prototypes: torch.FloatTensor = torch.stack(
all_class_prototypes, dim=0
).unsqueeze(
0
) # -> [1, n, features]
return all_class_prototypes
之后计算距离,再计算两者距离最小的下标即为预测。
def get_protonet_accuracy(
prototypes: torch.FloatTensor,
embeddings: torch.FloatTensor,
targets: Union[torch.Tensor, torch.LongTensor],
jsd: bool = False,
mahala: bool = False,
) -> torch.FloatTensor:
sq_distances = torch.sum(
(prototypes.unsqueeze(1) - embeddings.unsqueeze(2)) ** 2, dim=-1
)
_, predictions = torch.min(sq_distances, dim=-1)
return get_accuracy(predictions, targets)