动手学习pytorch之【CNN】——基础模型代码实现

Convolutional-NN

Simple-CNN

如果想看原理的话，请看我的同专栏下的文章

• 一个简单的多输入通道运行过程示意图：
  
  基础实现：

import torch
from torch import nn
from d2l import torch as d2l


# 自定义的二维互相关操作
def corr2d(X, K):
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y


# 自定义卷积层
class Conv2D(nn.Module):
    def __init__(self, kernel_size):  # kernel_size 是二维的
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))  # 广播

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias


# Part A  单通道卷积
X = torch.ones((6, 8))
X[:, 2:6] = 0
K = torch.tensor([[1.0, -1.0]])
Y = corr2d(X, K)  # 目标值

# 二维卷积层一般都使用四维输入和输出格式（批量大小、通道、高度、宽度）
X = X.reshape((1, 1, 6, 8))  # # 其中批量大小和通道数都为1
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  # 学习率

# 实现自学习的卷积核（忽略偏置），这里调用nn模块中的类
# 二维卷积，输入和输出通道都是1，相当于P=D=1，U和V通过结合kernel_size计算得到
# padding = P, stride = S, output: ( −  + 2) / + 1
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)
for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核，注意要data
    # 之前都是直接updatar.step()，因为迭代器中有根据grad更新参数的代码
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i + 1}, loss {l.sum():.3f}')


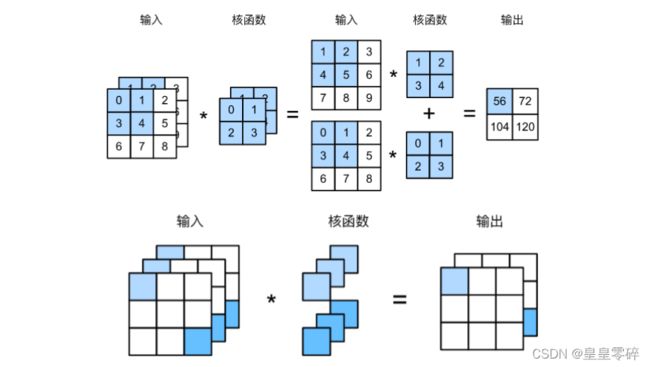
# Part B 多通道卷积
# 实现多输入通道的互相关操作，遍历每个通道维度后相加
def corr2d_multi_in(X, K):
    return sum(d2l.corr2d(x, k) for x, k in zip(X, K))


# 实现多输出通道的互相关操作,将每组卷积核卷积后的结果拼接起来
def corr2d_multi_in_out(X, K):
    # 沿着一个新维度对输入张量序列进行连接, dim=0指第0维(如1*2*2 拼接成 n*2*2)
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)


# 用全连接层实现1*1卷积
def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape  # torch.Size([3, 3, 3])
    c_o = K.shape[0]  # torch.Size([2, 3, 1, 1])
    X = X.reshape((c_i, h * w))  # torch.Size([3, 9])
    K = K.reshape((c_o, c_i))  # torch.Size([2, 3])
    # 全连接层中的矩阵乘法
    Y = torch.matmul(K, X)
    return Y.reshape((c_o, h, w))  # torch.Size([2, 9]) / 2*(3*3)


X = torch.normal(0, 1, (3, 3, 3))  # in_channel = 3
K = torch.normal(0, 1, (2, 3, 1, 1))  # out_channel = 2
Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6


# Part C 汇聚层
def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y


# 默认情况下深度学习框架中的步幅与汇聚窗口的大小相同
X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))  # 手动设置

Lanet模型实现：（这里暂且去掉最后一层高斯激活，用到了GPU）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sybPqgnP-1650811705618)(C:\Users\86130\AppData\Roaming\Typora\typora-user-images\image-20220423183942117.png)]

net = nn.Sequential(  # (M-K+2P)/S+1
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),  # C1: 6@28*28
    nn.AvgPool2d(kernel_size=2, stride=2),  # S2: 6@14*14
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),  # C3: 16@10*10
    nn.AvgPool2d(kernel_size=2, stride=2),  # S4: 16@5*5
    nn.Flatten(),  # 展平，以进行全连接 1*400
    nn.Linear(16*5*5, 120), nn.Sigmoid(),  # 全连接层F5: 400*120
    nn.Linear(120, 84), nn.Sigmoid(),  # 全连接层F6: 120*84
    nn.Linear(84, 10))  # 输出out: 84*10


# 使用GPU计算模型在数据集上的精度
def evaluate_accuracy_gpu(net, data_iter, device=None):
    if isinstance(net, nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(X, list):
                # BERT微调所需的
                X = [x.to(device) for x in X]
            else:
                X = X.to(device)
            y = y.to(device)
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]


# 用GPU训练模型
def train_ch(net, train_iter, test_iter, num_epochs, lr, device):
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)  # z
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')


X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'output shape: \t', X.shape)


batch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size=batch_size)
lr, num_epochs = 0.9, 10
train_ch(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())