动手实现一个带自动微分的深度学习框架

动手实现一个带自动微分的深度学习框架

转自：Automatic Differentiation Tutorial

参考代码：https://github.com/borgwang/tinynn-autograd (主要看 core/tensor.py 和 core/ops.py)

目录

• 简介
• 自动求导设计
• 自动求导实现
• 一个例子
• 总结
• 参考资料

---

简介

梯度下降（Gradient Descent）及其衍生算法是神经网络训练的基础，梯度下降本质上就是求解损失关于网络参数的梯度，不断计算这个梯度对网络参数进行更新。现代的神经网络框架都实现了自动求导的功能，只需要要定义好网络前向计算的逻辑，在运算时自动求导模块就会自动把梯度算好，不用自己手写求导梯度。

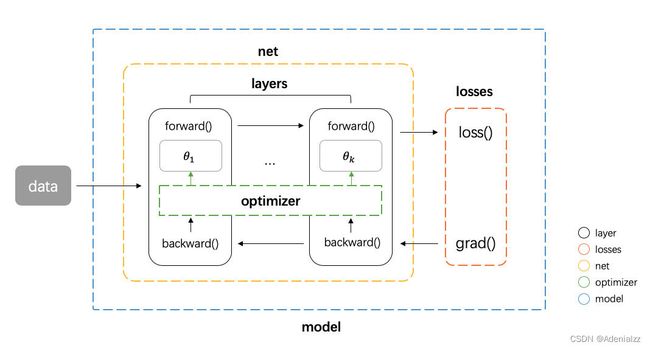
笔者在之前的 一篇文章 中讲解和实现了一个迷你的神经网络框架 tinynn，在 tinynn 中我们定义了网络层 layer 的概念，整个网络是由一层层的 layer 叠起来的（全连接层、卷积层、激活函数层、Pooling 层等等），如下图所示

在实现的时候需要显示为每层定义好前向 forward 和反向 backward（梯度计算）的计算逻辑。从本质上看 这些 layer 其实是一组基础算子的组合，而这些基础算子（加减乘除、矩阵变换等等）的导函数本身都比较简单，如果能够将这些基础算子的导函数写好，同时把不同算子之间连接逻辑记录（计算依赖图）下来，那么这个时候就不再需要自己写反向了，只需要计算损失，然后从损失函数开始，让梯度自己用预先定义好的导函数，沿着计算图反向流动即可以得到参数的梯度，这个就是自动求导的核心思想。tinynn 中之所有 layer 这个概念，一方面是符合我们直觉上的理解，另一方面是为了在没有自动求导的情况下方便实现。有了自动求导，我们可以抛开 layer 这个概念，神经网络的训练可以抽象为定义好一个网络的计算图，然后让数据前向流动，让梯度自动反向流动（ TensorFlow 这个名字起得相当有水准）。

我们可以看看 PyTorch 的一小段核心的训练代码（来源官方文档 MNIST 例子）

for batch_idx, (data, target) in enumerate(train_loader):
    data, target = data.to(device), target.to(device)
    optimizer.zero_grad()  # 初始化梯度
    output = model(data)  # 从 data 到 output 的计算图
    loss = F.nll_loss(output, target) # 从 output 到 loss 的计算图
    loss.backward()  # 梯度从 loss 开始反向流动
    optimizer.step()  # 使用梯度对参数更新

可以看到 PyTorch 的基本思路和我们上面描述的是一致的，定义好计算图 -> forward 得到损失 -> 梯度反向流动。

自动求导设计

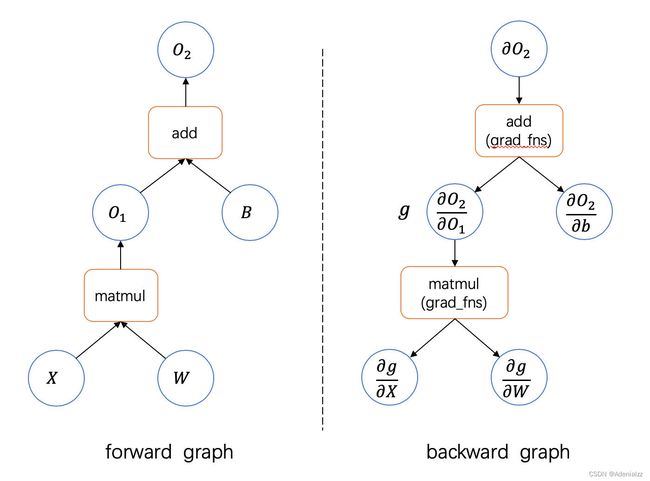
知道了自动求导的基本流程之后，我们考虑如何来实现。先考虑没有自动求导，为每个运算手动写 backward 的情况，在这种情况下我们实际上定义了两个计算图，一个前向一个反向，考虑最简单的线性回归的运算 $WX+B$，其计如下所示。

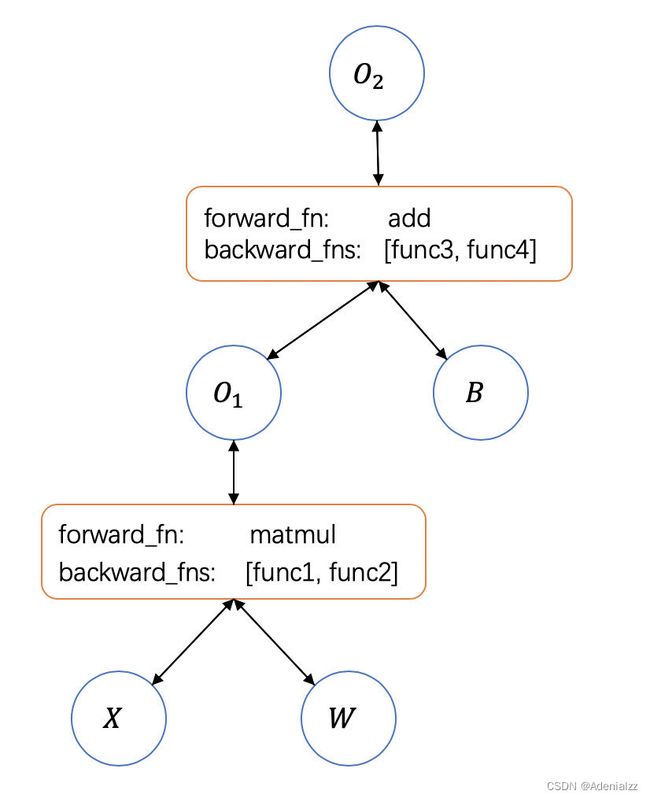
可以看到这两个计算图的结构实际上是一样的，只是在前向流动的是计算的中间结果，反向流动的是梯度，以及中间的运算反向的时候是导数运算。实际上我们可以把两者结合到一起，只定义一次前向计算图，让反向计算图自动生成

从实现的角度看，如果我们不需要自动求导，那么网络框架中的 Tensor 类只需要对 Tensor 运算符有定义，能够进行数值运算（tinynn 中就简单的使用 ndarray 作为 Tensor 的实现）。但如果要实现自动求导，那么 Tensor 类需要额外做几件事：

1. 增加一个梯度的变量保存当前 tensor 的梯度
2. 保存当前 tensor 依赖的 tensor（如上图中 O1O1 依赖于 X,WX,W）
3. 保存下对各个依赖 tensor 的导函数（这个导函数的作用是将当前 tensor 的梯度传到依赖的 tensor 上）

自动求导实现

我们按照上面的分析开始实现 Tensor 类如下，初始化方法中首先把 tensor 的值保存下来，然后有一个 requires_grad 的 bool 变量表明这个 tensor 是不是需要求梯度，还有一个 dependency 的列表用于保存该 tensor 依赖的 tensor 以及对于他们的导函数。

zero_grad() 方法比较简单，将当前 tensor 的梯度设置为 0，防止梯度的累加。自动求导从调用计算图的最后一个节点 tensor 的 backward() 方法开始（在神经网络中这个节点一般是 loss）。backward() 方法主要流程为

• 确保改 tensor 确实需要求导 self.requires_grad == True
• 将从上个 tensor 传进来的梯度加到自身梯度上，如果没有（反向求导的起点 tensor），则将梯度初始化为 1.0
• 对每一个依赖的 tensor 运行保存下来的导函数，计算传播到依赖 tensor 的梯度，然后调用依赖 tensor 的 backward() 方法。可以看到这其实就是 Depth-First Search 计算图的节点

def as_tensor(obj):
    if not isinstance(obj, Tensor):
        obj = Tensor(obj)
    return obj


class Tensor:

    def __init__(self, values, requires_grad=False, dependency=None):
        self._values = np.array(values)
        self.shape = self.values.shape

        self.grad = None
        if requires_grad:
            self.zero_grad()
        self.requires_grad = requires_grad

        if dependency is None:
            dependency = []
        self.dependency = dependency

    @property
    def values(self):
        return self._values

    @values.setter
    def values(self, new_values):
        self._values = np.array(new_values)
        self.grad = None

    def zero_grad(self):
        self.grad = np.zeros(self.shape)

    def backward(self, grad=None):
        assert self.requires_grad, "Call backward() on a non-requires-grad tensor."
        grad = 1.0 if grad is None else grad
        grad = np.array(grad)

        # accumulate gradient
        self.grad += grad

        # propagate the gradient to its dependencies
        for dep in self.dependency:
            grad_for_dep = dep["grad_fn"](grad)
            dep["tensor"].backward(grad_for_dep)

可能看到这里读者可能会疑问，一个 tensor 依赖的 tensor 和对他们的导函数（也就是 dependency 里面的东西）从哪里来？似乎没有哪一个方法在做保存依赖这件事。

假设我们可能会这样使用我们的 Tensor 类

W = Tensor([[1], [3]], requires_grad=True)  # 2x1 tensor
X = Tensor([[1, 2], [3, 4], [5, 6], [7, 8]], requires_grad=True)  # 4x2 tensor
O = X @ W  # suppose to be a 4x1 tensor

如何让 X 和 W 完成矩阵乘法输出正确的 O 的同时，让 O 能记下他依赖于 W 和 X 呢？答案是重载运算符。

class Tensor:
    # ...
    def __matmul__(self, other):
        # 1. calculate forward values
        values = self.values @ other.values

        # 2. if output tensor requires_grad
        requires_grad = ts1.requires_grad or ts2.requires_grad

        # 3. build dependency list
        dependency = []
        if self.requires_grad:
            # O = X @ W
            # D_O / D_X = grad @ W.T
            def grad_fn1(grad):
            	return grad @ other.values.T
            dependency.append(dict(tensor=self, grad_fn=grad_fn1))
        if other.requires_grad:
            # O = X @ W
            # D_O / D_W = X.T @ grad
			def grad_fn2(grad):
            	return self.values.T @ grad
            dependency.append(dict(tensor=other, grad_fn=grad_fn2))
        return Tensor(values, requires_grad, dependency)
    # ...

关于 Python 中如何重载运算符这里不展开，读者有兴趣可以参考官方文档或者这篇文章。基本上在 Tensor 类内定义了 __matmul__ 这个方法后，实际上是重载了矩阵乘法运算符 @ （Python 3.5 以上支持） 。当运行 X @ W 时会自动调用 X 的 __matmul__ 方法。

这个方法里面做了三件事：

1. 计算矩阵乘法结果（这个是必须的）

2. 确定是否需要新生成的 tensor 是否需要梯度，这个由两个操作数决定。比如在这个例子中，如果 W 或者 X 需要梯度，那么生成的 O也是需要计算梯度的（这样才能够计算 W 或者 X 的梯度）

3. 建立 tensor 的依赖列表

   自动求导中最关键的部分就是在这里了，还是以 O = X @ W 为例子，这里我们会先检查是否 X需要计算梯度，如果需要，我们需要把导函数 D_O / D_X 定义好，保存下来；同样的如果 W 需要梯度，我们将 D_O / D_W 定义好保存下来。最后生成一个 dependency 列表保存着在新生成的 tensor O 中。

然后我们再回顾前面讲的 backward()方法，backward() 方法会遍历 tensor 的 dependency ，将用保存的 grad_fn 计算要传给依赖 tensor 的梯度，然后调用依赖 tensor 的 backward() 方法将梯度传递下去，从而实现了梯度在整个计算图的流动。

grad_for_dep = dep["grad_fn"](grad)
dep["tensor"].backward(grad_for_dep)

自动求导讲到这里其实已经基本没有什么新东西，剩下的工作就是以类似的方法大量地重载各种各样的运算符，使其能够 cover 住大部分所需要的操作（基本上照着 NumPy 的接口都给重载一次就差不多了 ）。无论你定义了多复杂的运算，只要重载了相关的运算符，就都能够自动求导了，再也不用自己写梯度了。

一个例子

大量的重载运算符的工作在文章里就不贴上来了（过程不怎么有趣），我写在了一个 notebook 上，大家有兴趣可以去看看 borgwang/toys/ml-autograd。在这个 notebook 里面重载了实现一个简单的线性回归需要的几种运算符，以及一个线性回归的例子。这里把例子和结果贴上来

# training data
x = Tensor(np.random.normal(0, 1.0, (100, 3)))
coef = Tensor(np.random.randint(0, 10, (3,)))
y = x * coef - 3

params = {
    "w": Tensor(np.random.normal(0, 1.0, (3, 3)), requires_grad=True),
    "b": Tensor(np.random.normal(0, 1.0, 3), requires_grad=True)
}

learng_rate = 3e-4
loss_list = []
for e in range(101):
    # set gradient to zero
    for param in params.values():
        param.zero_grad()

    # forward
    predicted = x @ params["w"] + params["b"]
    err = predicted - y
    loss = (err * err).sum()

    # backward automatically
    loss.backward()

    # updata parameters (gradient descent)
    for param in params.values():
        param -= learng_rate * param.grad

    loss_list.append(loss.values)
    if e % 10 == 0:
        print("epoch-%i \tloss: %.4f" % (e, loss.values))

epoch-0 	loss: 8976.9821
epoch-10 	loss: 2747.4262
epoch-20 	loss: 871.4415
epoch-30 	loss: 284.9750
epoch-40 	loss: 95.7080
epoch-50 	loss: 32.9175
epoch-60 	loss: 11.5687
epoch-70 	loss: 4.1467
epoch-80 	loss: 1.5132
epoch-90 	loss: 0.5611
epoch-100 	loss: 0.2111

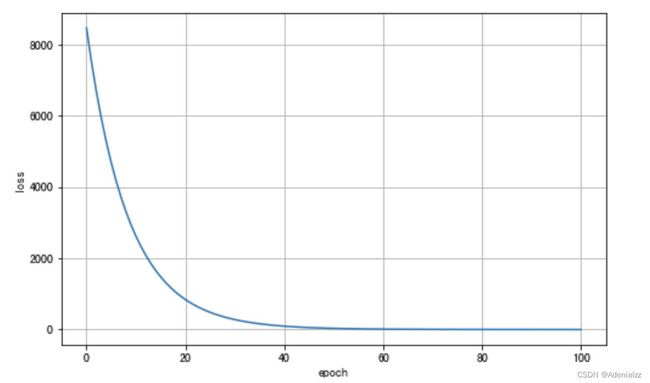
接口和 PyTorch 相似，在每个循环里面首先将参数梯度设为 0 ，然后定义计算图，然后从 loss 开始反向传播，最后更新参数。从结果可以看到 loss 随着训练进行非常漂亮地下降，说明我们的自动求导按照我们的设想 work 了。

总结

本文实现了讨论了自动求导的设计思路和整个过程是怎么运作的。总结起来：自动求导就是在定义了一个有状态的计算图，该计算图上的节点不仅保存了节点的前向运算，还保存了反向计算所需的上下文信息。利用上下文信息，通过图遍历让梯度在图中流动，实现自动求节点梯度。

我们通过重载运算符实现了一个支持自动求导的 Tensor 类，用一个简单的线性回归 demo 测试了自动求导。当然这只是最基本的能实现自动求导功能的 demo，从实现的角度上看还有很多需要优化的地方（内存开销、运算速度等），笔者有空会继续深入研究，读者如果有兴趣也可以自行查阅相关资料。Peace out.

参考资料

• PyTorch Doc
• PyTorch Autograd Explained - In-depth Tutorial
• joelgrus/autograd
• Automatic Differentiation in Machine Learning: a Survey