Harris角点检测原理

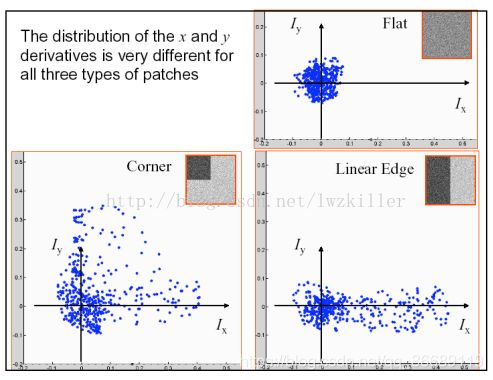
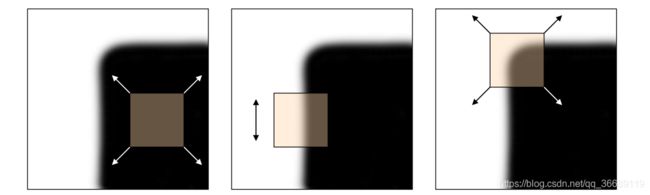
Harris角点检测是基于Moravec角点检测之上的， Moravec角点检测算子的思想其实特别简单，在图像上取一个W*W的“滑动窗口”，不断的移动这个窗口并检测窗口中的像素变化情况E。像素变化情况E可简单分为以下三种：A 如果在窗口中的图像是什么平坦的，那么E的变化不大。B 如果在窗口中的图像是一条边，那么在沿这条边滑动时E变化不大，而在沿垂直于这条边的方向滑动窗口时，E的变化会很大。 C 如果在窗口中的图像是一个角点时，窗口沿任何方向移动E的值都会发生很大变化。

用数学表达式就是：

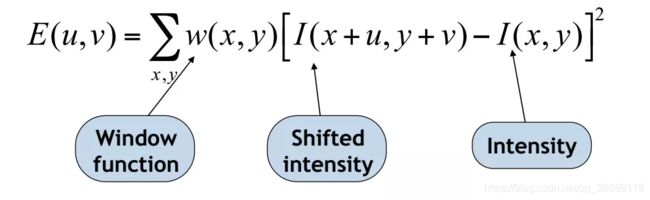
（u，v）就表示四个移动方向（1，0）（1，1）（0，1）（-1，1）,其中w为窗函数（window function），I为图像梯度，那么E就表示了灰度变化的剧烈程度

1977年，Moravec最先提出了如下的角点检测方法：

1. 对于原始图像，取偏移量(Δx,Δy)为(1,0),(1,1),(0,1),(-1,1)，分别计算每一像素点(xi,yi)的灰度变化
2. 对于每一像素点(xi,yi)，计算角点响应函数R(xi,yi)=min E
3. 设定阈值T，将角点响应函数R(xi,yi)中低于T的值设为0
4. 在窗口范围内进行非极大值抑制：遍历角点响应函数，若某个像素的角点响应函数在窗口内不是最大，该像素置0
5. 选择非零点作为角点检测结果

Moravec角点检测的缺点

1. 二值的窗口函数导致角点响应函数不够光滑
2. 只在四个方向上计算灰度值变化，导致角点响应函数在多处都有较大响应
3. 对于每个点只考虑E的最小值，导致算法对边缘有很强的反应

1988年，Harris和Plessey对Moravec的方法进行了改进，提出了经典的Harris角点检测算法。Harris首先将Moravec算法中的窗口函数由阶跃函数改为二维高斯函数，并通过泰勒展开考察微小移动，也就是说，如果要求E的最大值以明确角点，就可以令$u,v\to 0$，对E做泰勒展开，得

$$E(u,v)=(u,v)M\left(\begin{array}{l}u\\ v\end{array}\right)$$
$$M=\sum _{(x,y)}w(x,y)\left(\begin{array}{cc}{I}_X^2& I_X{I}_Y\\ I_X{I}_Y& I_Y^2\end{array}\right)=\left(\begin{array}{cc}{\sum }_W{I}_X^2& {\sum }_W{I}_X{I}_Y\\ {\sum }_W{I}_X{I}_Y& {\sum }_W{I}_Y^2\end{array}\right)$$

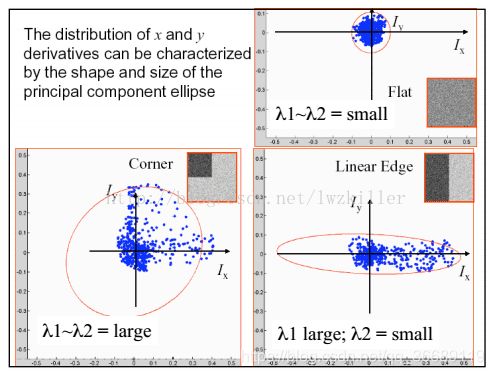
记 $M=\left(\begin{array}{ll}A& B\\ B& C\end{array}\right)$，则上式可以写成 $A{u}^2+2Buv+C{v}^2=E$ 的形式，这表示了一个椭圆，自相关矩阵M描述了图像局部区域的灰度变化趋势，可以通过椭圆的形状来判定角点。
下面解释下上面的内容：
1.窗口函数的两种形式：

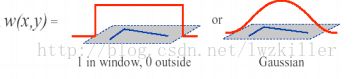
2.泰勒公式展开：
，任何一个函数表达式，均可有泰勒公式进行展开，以逼近原函数，我们可以对下面函数进行一阶展开:
$$f(x+u,y+v)\approx f(x,y)+u{f}_x(x,y)+v{f}_y(x,y)$$
那么：
$$\sum [I(x+u,y+v)-I(x,y){]}^2$$
$$\approx \sum {\left[I(x,y)+u{I}_x+v{I}_y-I(x,y)\right]}^2$$
$$=\sum u^2{I}_x^2+2uv{I}_x{I}_y+v^2{I}_y^2$$
$$=\sum \left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]\left[\begin{array}{l}u\\ v\end{array}\right]$$
$$=\left[\begin{array}{ll}u& v\end{array}\right]\left(\sum \left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]\right)\left[\begin{array}{l}u\\ v\end{array}\right]$$

把中间看成矩阵M，则：
$$E(u,v)\cong [u,v]M\left[\begin{array}{l}u\\ v\end{array}\right]$$

$$M=\left[\begin{array}{cc}\sum I_x^2& \sum I_x{I}_y\\ \sum I_x{I}_y& \sum I_y^2\end{array}\right]=\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]$$

现在回到椭圆函数那里，至于椭圆函数的得来，查到的是通过微分思想化简而来，具体的还没深究，
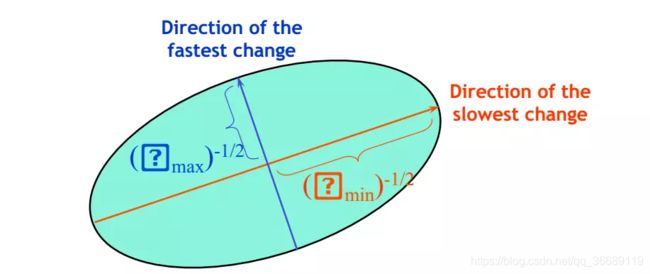
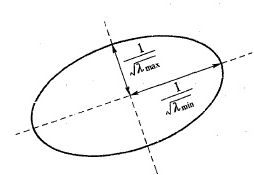
对于椭圆 $A{x}^2+2Bxy+C{y}^2=1$ ，设其半长轴和半短轴分别为a,b，那么$\frac{1}{\sqrt{a}},\frac{1}{\sqrt{b}}$ 是矩阵M的特征值。(特征值的含义见添加链接描述)

将上面的点用一个椭圆轮廓包围

得到M的特征值有什么用呢？若用奇异值分解的观点看这个问题。由于Jacobian矩阵 $J=\left(\begin{array}{l}{I}_X\\ I_Y\end{array}\right)$，故M=JJ^T，这样M的特征值开根号后就是J的奇异值，因此M的特征值就可以体现IX和IY的相对大小。

现在我们需要定义角点响应函数，进一步进行区分，令（一般k=0.04 ~ 0.06）
$$R=\det (M)-k{\mathrm{tr}}^2(M)$$
$$M=\left[\begin{array}{cc}\sum I_x^2& \sum I_x{I}_y\\ \sum I_x{I}_y& \sum I_y^2\end{array}\right]=\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]$$
其中：
$\det (M)={\lambda }_1{\lambda }_2={\sum }_W{I}_X^2\cdot {\sum }_W{I}_Y^2-{\left({\sum }_W{I}_X{I}_Y\right)}^2$
$\mathrm{tr}(M)={\lambda }_1+{\lambda }_2={\sum }_W{I}_X^2+{\sum }_W{I}_Y^2$

一般增大k的值，将减小角点响应值R，降低角点检测的灵性，减少被检测角点的数量；减小k值，将增大角点响应值R，增加角点检测的灵敏性，增加被检测角点的数量。

参考博客：
https://www.jianshu.com/p/6ae09c3d226f
https://blog.csdn.net/newthinker_wei/article/details/45603583
https://zhuanlan.zhihu.com/p/42490675
https://zhuanlan.zhihu.com/p/36382429
https://blog.csdn.net/fengye2two/article/details/79119736