手眼标定学习总结：原理、Tsai方法和Matlab代码

本文仅用于记录自己学习手眼标定过程的一些总结。

手眼标定基本原理

符号统一：
$T_x^y$或T_y_x表示将一个点从x系的坐标转移到y系的坐标，后面一律用T_y_x形式，方便编辑。
T_c_t：从target（棋盘格）坐标系到camera坐标系，从图像计算得到
T_g_c：从camera到gripper（机械臂末端坐标系），这是手眼标定需要求的参数
T_b_g：从gripper到base（机械臂基底坐标系），从机械臂运动学方程得到
T_b_t：从target到base，一般是未知无法计算的
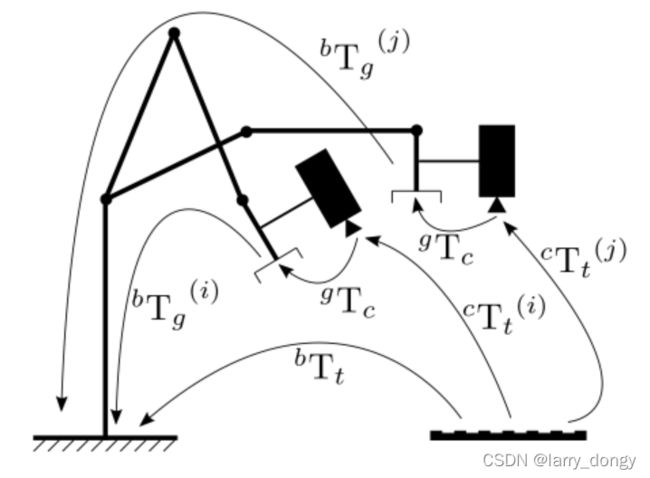计算时，由于T_b_t未知，所以无法直接求出T_g_c。但如果考虑增量（见下图），图中Hgij为G_ij，即gripper从第 i 个位置到 j 个位置，Hcij为C_ij，相机位置的增量（此图来自于参考文献[1]，H表示的是Homogeneous Transformation Matrix。且图中的Hcg为从camera到gripper，对应本文中的T_g_c）。红色和黄色最终表示同一个变换，所以此时有等式：$$G_{ij}\ast T_g^c=T_g^c\ast C_{ij}$$

最终camera和gripper达到多个位置后，得到多组 ij 对应关系，得到终极表达式：$$AX=XB$$

需要注意的是，X的含义与给的A和B有关。本文中，X为：T_g_c，A/B分别为G和C组成的$4\ast (4\ast N)$二维矩阵，即每4列为一个ij对应：$G_i=G(1:4,i\ast 4-3:i\ast 4)$（matlab写法）。

求解AX=XB

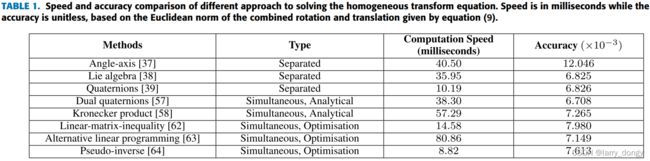
下面就是求解AX=XB这个方程。根据综述文[2]，求解主要有：seperated、simultaneous两种思路。

seperated方法
前者是首先计算出旋转量R，然后再计算t。将等式写成：

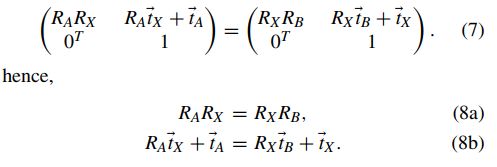
求解出Rx再计算tx。计算Rx时，又由于采用的旋转表示方式不同，又分为轴角、李代数、四元数等不同的解法。

simultaneous方法
seperated方法的问题是，R计算的误差，会传递给t。且理论上R和t是耦合的，分开计算不合理。所以有同时计算两个参数的方法，或解析的、或优化的求解$min||AX-XB||$。

详细内容请参考[2]综述。

Tsai方法

Tsai方法是seperated的轴角表示方法，详见论文[1]。这里不做推导，只给出计算方法：

1. 计算出Gij和Cij
2. Gij和Cij对应的轴角表示方法，记作Pgij, Pcij
3. 根据公式：$(skew(Pgij+Pcij)\ast Pc{g}^{\prime }=Pcij-Pgij)$计算出$Pc{g}^{\prime }$
4. 由$Pc{g}^{\prime }$计算出R_g_c
5. 由$((R_{gij}-I)\ast t_c^g=R_{cg}\ast t_{cij}-t_{gij}$计算出平移量t_g_c
6. 最终得到T_g_c = [R_g_c, t_g_c; 0,0,0, 1]
   

Tsai的Matlab代码实现

忘了从哪里找了一个代码（想起来补出处），对着论文公式，确定认了方法有效。并进行了验证。
完整代码的github链接：https://github.com/LarryDong/HandEye-Tsai

function X = tsai(A,B)
% Calculates the least squares solution of
% AX = XB
% 
% A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration. Lenz Tsai
% Mili Shah July 2014

% checked, modified and commented by LarryDong 2021.12.28
%
% Input: A/B: (4,4N) matrix (homogeneous transformation matrix, (R, t | 0, 1) )
% Output: X: (4,4), AX = XB
%
% For hand-eye calibration, 
% X: T_g_c, transform a point from camera to gripper 
% A(4, i*4-3:i*4): homogeneous transformation from gripper_i to gripper_j
% B(4, i*4-3:i*4): homogeneous transformation from camera_i to camera_j
% The equation `AX=XB` is based on rigid body transformation assumption.

[m,n] = size(A); n = n/4;
S = zeros(3*n,3);
v = zeros(3*n,1);

%% Calculate best rotation R
for i = 1:n
    A1 = logm(A(1:3,4*i-3:4*i-1));                  % 计算旋转对应的反对称矩阵：exp(\phi^)=Aij，其中\phi^是旋转轴\phi的反对称矩阵，即下面的a
    B1 = logm(B(1:3,4*i-3:4*i-1));                  % calculate the skew matrix of a rotation: exp(\phi^)=Aij, where \phi& is the skew matrix of aixs-rotation \phi (is `a` in next lines)
    a = [A1(3,2) A1(1,3) A1(2,1)]'; a = a/norm(a);  % 计算旋转向量增量 a_ij
    b = [B1(3,2) B1(1,3) B1(2,1)]'; b = b/norm(b);  % calculate the rotation vector (axis) increasement a_ij
    S(3*i-2:3*i,:) = skew(a+b);                     % 对应论文的公式(12)中的Skew(Pgij+Pcij)    Eq.12 in reference paper, Skew(Pgij+Pcij)
    v(3*i-2:3*i,:) = a-b;                           % 对应论文的公式(12)中的Pcij-Pgij    Eq.12 in reference paper, Pcij-Pgij
end

x = S\v;                            % x is Pcg' in Eq.12
theta = 2*atan(norm(x));
eps = 0.0000000001;                      % avoid divide-by-zero. Added by LarryDong
x = x/(norm(x)+eps);
R = (eye(3)*cos(theta) + sin(theta)*skew(x) + (1-cos(theta))*x*x')';    % Rodrigues. (Eq.10)

%% Calculate best translation t
% This paper first calculate R then t, in a seperate procedure. Eq. 15
C = zeros(3*n,3);
d = zeros(3*n,1);
I = eye(3);

for i = 1:n
    C(3*i-2:3*i,:) = I - A(1:3,4*i-3:4*i-1);    % C is (Rgij-I) in Eq. 15       (Negative on both side)
    d(3*i-2:3*i,:) = A(1:3,4*i)-R*B(1:3,4*i);   % d is (RcgTcij - Tgij) in Eq. 15
end

t = C\d;
X = [R t;0 0 0 1];
end

%% other functions.
function Sk = skew( x )
   Sk = [0,-x(3),x(2);x(3),0,-x(1);-x(2),x(1),0];
end

验证思路如下：随机给定（或通过image计算出）一些列的T_c_t，然后假设T_g_c是某个数值，计算出理论的T_b_g。然后再用T_b_g和T_c_t通过手眼标定计算T_g_c看是否与给定的相同。这可以避免T_b_g采集时和T_c_t计算错误的情况。

验证代码如下：

clc;clear;
%% load data
fid = fopen('target2cam.csv', 'r');
A =  textscan(fid, '%f,%f,%f,%f,%f,%f,%f');
rvecx = A{2};
rvecy = A{3};
rvecz = A{4};
tvecx = A{5};
tvecy = A{6};
tvecz = A{7};

%% set data
% T_b_t can be any value. No effection on results
R_b_t = [1, 0, 0;
        0, 1, 0;
        0, 0, 1];
t_b_t = [0, 0, 0]';
T_b_t = [R_b_t, t_b_t;
        0,0,0,  1];

% give "T_c_g" (or T_g_c) to generate the T_b_g
theta_x = pi/5;
theta_y = pi/6;
theta_z = pi/9;

rotX = [1, 0, 0;
        0, cos(theta_x), sin(theta_x);
        0, -sin(theta_x), cos(theta_x)];
rotY = [cos(theta_y), 0, -sin(theta_y);
        0, 1, 0;
        sin(theta_y), 0, cos(theta_y)];
rotZ = [cos(theta_z), sin(theta_z), 0;
        -sin(theta_z), cos(theta_z), 0;
        0, 0, 1];

R_c_g =  rotZ * rotY * rotX;
t_c_g = [1, 2, 3]';
T_c_g = [R_c_g, t_c_g; 
        0,0,0, 1];
T_g_c = inv(T_c_g);


%% generate grigper2base
N = 16;
T_b_g_list = zeros(4, 4, N);
T_t_c_list = zeros(4, 4, N);
for i = 1:N
%     fprintf("%d\n", i);
    r_c_t = [rvecx(i), rvecy(i), rvecz(i)]';
    t_c_t = [tvecx(i), tvecy(i), tvecz(i)]';
    
    R_c_t = Rodrigues(r_c_t);					% matlab貌似没有这个函数，需要自己实现
    
    T_c_t = [R_c_t, t_c_t; 
            0,0,0,  1];
    T_t_c = inv(T_c_t);
    
    T_b_g = T_b_t * T_t_c * T_c_g;      % generate T_b_g based on chain mul.
    
    T_t_c_list(:,:,i) = T_t_c;
    T_b_g_list(:,:,i) = T_b_g;
end

%% calculate Gij and Cij
Gij_list = [];
Cij_list = [];
i_idx = [1,2,3,4,5,6];
j_idx = [7,10,11,12,13,14];
for k = 1:length(i_idx)
    i = i_idx(k);
    j = j_idx(k);
    Gij = inv(T_b_g_list(:,:,i)) * T_b_g_list(:,:,j);
    Cij = inv(T_t_c_list(:,:,i)) * T_t_c_list(:,:,j);
    Gij_list = [Gij_list, Gij];
    Cij_list = [Cij_list, Cij];
end

X = tsai(Gij_list, Cij_list);

% X is T_g_c when given GX = XC
X
T_g_c
Error = norm(X - T_g_c)

运行结果：计算值和理论值相相同：

后记

最开始用python写，手眼标定的结果总是不正确。无奈之下，采用“验证”中的方法，给定了T_g_c真值，生成模拟的数据，然后再验证。但使用OpenCV的CalibrateHandEye函数，计算结果始终不正确，逻辑也查过了没有问题，故换成了Matlab，认真学习了手眼标定的原理，看了几篇论文，复现了Tsai方法，最终验证了正确。也不知道是不是python代码写的有问题，还是OpenCV的库有问题(OpenCV v4.5)。

参考文献

[1] R. Y. Tsai and R. K. Lenz, “A new technique for fully autonomous and efficient 3D robotics hand/eye calibration,” in IEEE Transactions on Robotics and Automation, vol. 5, no. 3, pp. 345-358, June 1989, doi: 10.1109/70.34770.

[2] I. Enebuse, M. Foo, B. S. K. K. Ibrahim, H. Ahmed, F. Supmak and O. S. Eyobu, “A Comparative Review of Hand-Eye Calibration Techniques for Vision Guided Robots,” in IEEE Access, vol. 9, pp. 113143-113155, 2021, doi: 10.1109/ACCESS.2021.3104514.