【机器学习杂烩】投票(Voting)算法在分类问题上的应用(一口气实现Logistic 回归、SVM、KNN、C4.5 决策树、 Adaboost、GBDT 和随机森林,并集成起来)
投票算法简介
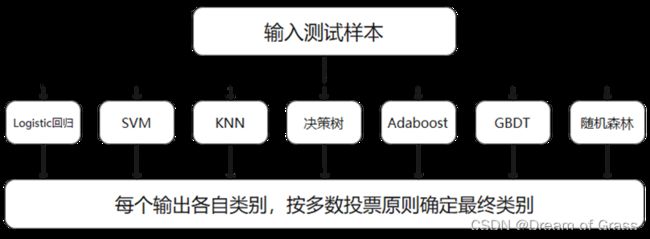
投票是在分类算法中广泛运用的集成学习算法之一。投票主要有硬投票和软投票 两种。硬投票即各基分类器权重相同的投票, 其原理为多数投票原则:如果基分类器 的某一分类结果超过半数, 则集成算法选择该结果; 若无半数结果则无输出。软投票 的原理也为多数投票, 但是各基分类器投票所占的权重可自己定义。当各基分类器分类效果差异比较大时, 应当选择软投票, 赋予基础分类器更大的权重, 从而获得更好 的分类性能, 以此优化分类结果。
基分类器介绍
本文选取的 7 种基分类器分别为: Logistic 回归、SVM、KNN、C4.5 决策树、 Adaboost、GBDT 和随机森林。
Logistic 回归
Logistic 回归属于非线性回归, 适用于研究分类与影响因素之间关系的多重回归方 去, 核心公式为: f ( x ) = 1 1 + e − x , f ( x ) f(x)=\frac{1}{1+e^{-x}}, f(x) f(x)=1+e−x1,f(x) 的范围为 ( 0 , 1 ) (0,1) (0,1) 。二分类变量的赋值将非糖尿 病患者定为 x = 0 x=0 x=0, 糖尿病患者定为 x = 1 x=1 x=1, 回归模型为 log i t ( p ) = δ 0 + δ 1 × x \log i t(p)=\delta_{0}+\delta_{1} \times x logit(p)=δ0+δ1×x, 则对非 溏尿病患者有 log i t ( p ) = δ 0 + δ 1 × 0 \log i t(p)=\delta_{0}+\delta_{1} \times 0 logit(p)=δ0+δ1×0 , 糖尿病患者有 log i t ( p ) = δ 0 + δ 1 × 1 \log i t(p)=\delta_{0}+\delta_{1} \times 1 logit(p)=δ0+δ1×1 。偏回归系数 δ 0 , δ 1 \delta_{0}, \delta_{1} δ0,δ1 的估计采用极大似然估计。在传统分类问题中, Logistic 模型准确率一般可达到 8 % 8 \% 8% 97%。
SVM
SVM 是一种二分类模型, 是定义在特征空间上的间隔最大的线性分类器, 由于样 本数远超特征维数,因此本题选用非线性 SVM,目标函数为:
{ min a ( 1 2 ∑ i = 1 n ∑ j = 1 n a i a j y i y j ( ∮ ( x i ) × ∮ ( x j ) ) − ∑ i = 1 n a i ) s.t. ∑ i = 1 0 ⩽ a i ⩽ C a i y i = 0 \left\{\begin{array}{l} \min _{a}\left(\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} a_{i} a_{j} y_{i} y_{j}\left(\oint\left(x_{i}\right) \times \oint\left(x_{j}\right)\right)-\sum_{i=1}^{n} a_{i}\right) \\ \text { s.t. } \sum_{\substack{i=1 \\ 0 \leqslant a_{i} \leqslant C}} a_{i} y_{i}=0 \end{array}\right. ⎩ ⎨ ⎧mina(21∑i=1n∑j=1naiajyiyj(∮(xi)×∮(xj))−∑i=1nai) s.t. ∑i=10⩽ai⩽Caiyi=0
将内积中 ∮ ( x i ) × ∮ ( x j ) \oint\left(x_{i}\right) \times \oint\left(x_{j}\right) ∮(xi)×∮(xj) 使用核函数替换, 计算出最优的 a i a_{i} ai, 可得到超平面的 w w w 和 b b b, 其 中, w w w 为法向量, 决定了超平面方向, b b b 是位移量, 可以决定超平面与原点之间的距离。
KNN
K N N \mathrm{KNN} KNN 是一种监督学习算法, 当预测一个新的值 x x x 的时候, 根据它距离最近的 k k k 个点 是什么类别来判断 x x x 属于哪个类别。先选取一个较小的 k k k 值, 不断增加 k k k 值, 验证集合的 方差, 找到比较合适的 k k k 值。距离选取多维的欧氏距离, 公式为: d ( x , y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + ⋯ + ( x n − y n ) 2 = ∑ i = 1 n ( x i − y i ) 2 d(x, y)=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\cdots+\left(x_{n}-y_{n}\right)^{2}}=\sqrt{\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}} d(x,y)=(x1−y1)2+(x2−y2)2+⋯+(xn−yn)2=i=1∑n(xi−yi)2
决策树
决策树可根据已知的分类结果对新的数据分类, 其树形结构的每个内部节点表示一 个属性上的判断, 每个分支代表一个判断结果的输出, 最后每个叶节点代表一种分类结 果。决策树可分为三类: ID3、C4.5 和 CART。本文选择了 C4.5 决策树, 以信息增益率 为准则来选择划分属性的决策树, 信息增益率:
Gain ratio ( D , a ) = Gain ( D , a ) I V ( a ) , I V ( a ) = − ∏ v = 1 v ∣ D v ∣ D log 2 ∣ D v ∣ D \text { Gain } \operatorname{ratio}(D, a)=\frac{\operatorname{Gain}(D, a)}{I V(a)}, \quad I V(a)=-\prod_{v=1}^{v} \frac{\left|D^{v}\right|}{D} \log _{2} \frac{\left|D^{v}\right|}{D} Gain ratio(D,a)=IV(a)Gain(D,a),IV(a)=−v=1∏vD∣Dv∣log2D∣Dv∣
Adaboost 和 GBDT
Adaboost, GBDT 和都是基于 boosting 算法的分类器, GBDT 分类首先初始化一个弱分类器, 计算损失函数的负梯度值, 再利用数据集拟合下一轮模型, 重复计算负梯 度值和拟合过程, 利用 m \mathrm{m} m 个基础模型, 构建梯度提升树。Adaboost 首先赋予 n \mathrm{n} n 个训 练样本相同的权重, 从而训练出一个基分类器, 之后进行预先设置的 T \mathrm{T} T 次迭代, 每次迭代将前一次分类器中分错的样本加大权重, 使得在下一次迭代中更加关注这些样本, 从而调整权重改善分类器, 经过 T \mathrm{T} T 次迭代得到 T \mathrm{T} T 个基分类器, 最终将这些基分类器线 性组合得到最终分类器模型。
随机森林
随机森林属于集成学习中的 Bagging (Bootstrap AGgregation 的简称) 方法, 是利用多棵决策树对样本进行训练并预测的一种分类器, 最后将分类结合为一个最终的结果, 其优于单个决策树做出的分类结果。
代码实现
导入所需的包
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import metrics
from sklearn import preprocessing
from sklearn.ensemble import AdaBoostClassifier as ada
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import RandomForestClassifier as RF
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
读取要分类的数据
data = pd.read_csv("D:/第三题/第三轮附件2_English.CSV")
data.head()
| Gender | Age | HDLcholesterol | LDLcholesterol | VLDLcholesterol | TG | TotalCholesterol | Pulse | DiastolicPressure | HistoryHypertension | UreaNitrogen | UricAcid | Creatinine | Weight | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 38 | 1.25 | 2.99 | 1.07 | 0.64 | 5.31 | 83 | 83 | 0 | 4.99 | 243.3 | 50 | 1 |
| 1 | 0 | 31 | 1.15 | 1.99 | 0.84 | 0.50 | 3.98 | 85 | 63 | 0 | 4.72 | 391.0 | 47 | 1 |
| 2 | 0 | 27 | 1.29 | 2.21 | 0.69 | 0.60 | 4.19 | 73 | 61 | 0 | 5.87 | 325.7 | 51 | 1 |
| 3 | 0 | 33 | 0.93 | 2.01 | 0.66 | 0.84 | 3.60 | 83 | 60 | 0 | 2.40 | 203.2 | 40 | 2 |
| 4 | 0 | 36 | 1.17 | 2.83 | 0.83 | 0.73 | 4.83 | 85 | 67 | 0 | 4.09 | 236.8 | 43 | 0 |
构造响应变量和预测变量
X = data[['Gender', 'Age', 'HDLcholesterol', 'LDLcholesterol',
'VLDLcholesterol', 'TG', 'TotalCholesterol', 'Pulse',
'DiastolicPressure', 'HistoryHypertension', 'UreaNitrogen', 'UricAcid',
'Creatinine', 'Weight']]
X.head()
y = data[['Diabetic']]
y.head()
数据标准化和训练集/测试集划分
X = preprocessing.StandardScaler().fit(X).transform(X.astype(float))
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=4)
print('Train set:', X_train.shape, y_train.shape)
print('Test set:', X_test.shape, y_test.shape)
Train set: (804, 3) (804, 1)
Test set: (202, 3) (202, 1)
构建基分类器模型
LR = LogisticRegression()
Ada = ada()
GBDT = GradientBoostingClassifier()
svc = SVC(probability=True)
rf = RF()
KNN = KNeighborsClassifier(n_neighbors=5)
Tree = DecisionTreeClassifier(criterion="entropy", max_depth=4)
硬投票
weight = []
for clf, label in zip([LR, Ada, GBDT, svc, rf, KNN, Tree],
['LR',
'Ada',
'GBDT',
'svc',
'rf',
'KNN',
'Tree']):
clf.fit(X_train, y_train)
y_predict = clf.predict(X_test)
print('{}在预测集模型的准确率为:\n'.format(label), metrics.accuracy_score(y_test, y_predict))
print('{}在训练集模型的准确率为:\n'.format(label), metrics.accuracy_score(y_train, clf.predict(X_train)))
print('{}的综合准确率为:\n'.format(label), metrics.accuracy_score(y, clf.predict(X)))
tem = metrics.accuracy_score(y, clf.predict(X))
weight.append(tem)
print('{}的 ROC 面积为:'.format(label), metrics.roc_auc_score(y, clf.predict(X)))
print()
软投票
weight = [0.132, 0.141, 0.154, 0.141, 0.159, 0.138, 0.131]
vote2 = VotingClassifier(
estimators=[('LR', LR), ('Ada', Ada), ('GBDT', GBDT), ('SVC', svc), ('rf', rf), ('KNN', KNN), ('Tree', Tree)],
voting='soft', weights=weight)
vote2.fit(X_train, y_train)
y_predict = vote2.predict(X_test)
print('{}在预测集模型的准确率为:\n'.format('soft Voting'), metrics.accuracy_score(y_test, y_predict))
print('{}在训练集模型的准确率为:\n'.format('soft Voting'), metrics.accuracy_score(y_train, vote2.predict(X_train)))
print('soft voting 的综合表现:\n', metrics.accuracy_score(y, vote2.predict(X)))
print()
P = vote2.predict_proba(X)[:, 1]
fpr, tpr, threshold = metrics.roc_curve(y, P)
roc_auc = metrics.auc(fpr, tpr)
plt.figure(figsize=(6, 4), dpi=250)
plt.stackplot(fpr, tpr, color='steelblue', alpha=0.5, edgecolor='black')
plt.plot(fpr, tpr, color='black', lw=1)
plt.plot([0, 1], [0, 1], color='red', linestyle='--')
plt.text(0.5, 0.3, 'ROC curve (area = %0.4f)' % roc_auc, fontsize=10)
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
plt.show()
最后结果
每个分类器及voting模型运行代码即可,我就贴一个最后的ROC曲线图吧。
上面的代码都是可以运行的,大家觉得好的话,您的点赞收藏就是对我最大的鼓励!谢谢大家~
