基于affine+sift特征提取的图像配准算法matlab仿真

目录

一、理论基础

二、核心程序

三、仿真测试结果

---

一、理论基础

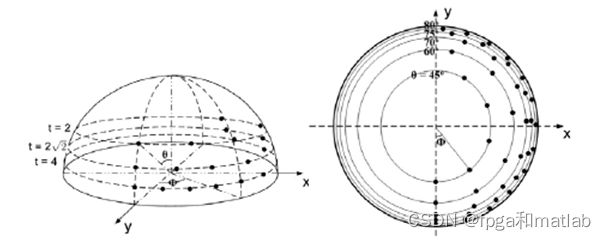
       由于相机正面拍摄物体时，相机的光轴方向可能发生变化，带来扭曲，所以第一步是对每张图片进行变换，模拟所有可能的仿射扭曲。这些扭曲由两个参量决定：水平角度φ 和垂直角度θ 。将图像旋转φ 度由倾斜度参数 t 完成：t  = 1 cosθ。设原始图像为 u ( x , y )，原始图像在 X 轴上倾斜度为 t 的变换由 u ( x , y ) → u (t x , y)得到。对数字图像来说，倾斜图像由具有方向性的 t 倍二次采样(t-subsampling)得到。它要求之前在 X 轴上有一次抗走样处理(antialiasing filter)，最大限度的减少图像失真。该滤波由标准差为c的高斯卷积完成。在文献[1]中 Lowe 建议该值取c = 0.8。文献[15]中证明了该取值图像失真度较小。对图像进行旋转变换和倾斜变换可以模拟有限的一些不同水平角度，垂直角度拍摄图像。对这些参数进行采样能保证模拟图像在不同的φ 和θ 引起的视角变换下保持近似。所有模拟倾斜后的图像将由 SIFT 算法进行匹配比较。

 

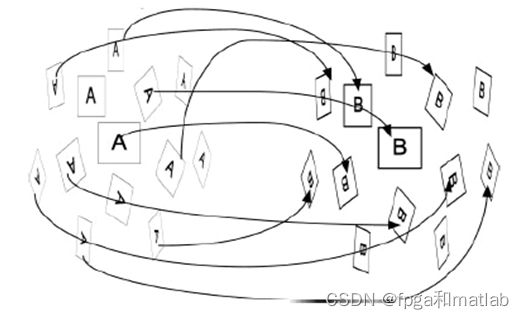
         图显示了 ASIFT 算法概貌：正方形 A,B 分别代表被比较的图像 u 和 v。ASIFT 算法模拟了所有相机视轴坐标方向变化引起的扭曲。图中的平行四边形代表模拟扭曲后的图像，该图像将运用 SIFT 进行后续的匹配计算。

采样范围

     倾斜度参数 t 的采样范围非常关键。只有当目标是一个完美的二维平面，或者是个反射光强弱完全相同的物体时，才有可能在任何倾斜视角下做到目标识别。现实中找不到这样的物体。因此，需要通过实验比较室内外拍摄的图片对，并找出可行的 t 的上界。每对图片由正面视角拍摄的图片和倾斜角度拍摄的图片组成。

采样步骤:

     为使 ASIFT 算法对任何仿射变换具有不变性，倾斜度t和角度φ 必须具有较高精度。采样间隔由自然图像的多次实验得到。

二、​​​​​​​核心程序

clc;
clear;
close all;
warning off;
addpath 'func\'
% RandStream.setDefaultStream(RandStream('mt19937ar','seed',1));


FIG           = 1;



%1的话设置连线，0的话这对你的问题一，显示特征点
Feature_point = 1;
%是否需要重新特征提取,%1:对以一组新的图片，需要选择1，对于同一组图片，直接设置0
sel     = 1;
t       = sqrt(2).^([0]);%选择不同的角度t，arccos(1/t);

%读取图片
img1 = imread('a.jpg');
img2 = imread('b3.jpg');

%转换为灰度图
[R,C,K] = size(img1);
if K == 3
    img1s = rgb2gray(img1);
else
    img1s = img1;
end

[R,C,K] = size(img2);
if K == 3
    img2s = rgb2gray(img2);
else 
    img2s = img2;
end


figure;
subplot(121);imshow(img1s);title('原始图片1');
subplot(122);imshow(img2s);title('原始图片2');
%计算图片的大小
[m1,n1] = size(img1s);
[m2,n2] = size(img2s);

%对两个图片分别进行角度选择和不同角度的特征提取
if sel == 1
     tic;
     disp('对图片1进行处理');
     [Hrl_feature1,Hr_pointl_feature1,cnt1]=func_sift_angle(img1s,m1,n1,t);
     Time = toc;
     disp('对图片2进行处理');
     [Hrl_feature2,Hr_pointl_feature2,cnt2]=func_sift_angle(img2s,m2,n2,t);
     save feature_data_B1.mat  Hrl_feature1 Hr_pointl_feature1 Hrl_feature2 Hr_pointl_feature2 cnt1 cnt2 Time
else
     load feature_data_B1.mat     
end

%进行配准
pp           = 0;
level        = 0.6; 
image_match1 = []; 
image_match2 = []; 
for i = 1:(cnt1 - 1)
    for j = 1:(cnt2 -1)
    pp = pp + 1;
    fprintf('处理进度：');fprintf('%3.2f',100*pp/(cnt1*cnt2));fprintf('%%\n\n');  
    NF1(i)       = size(Hrl_feature1{i},1);
    NF2(j)       = size(Hrl_feature2{j},1);
    same_feature = func_feature_match(Hrl_feature1{i},Hrl_feature2{j},level);            
    ind1         = find(same_feature);
    ind2         = same_feature(ind1);
    %根据门限来选择一定区域内的配准点
    ind          = find(sqrt(sum(((Hrl_feature1{i}(ind1,:)-Hrl_feature2{j}(ind2,:)).^2),2)) <= level);
    
    ind1         = ind1(ind);
    ind2         = ind2(ind);
    Match1Tmp    = Hr_pointl_feature1{i}(ind1,[ 1 2 3 end ]);
    Match2Tmp    = Hr_pointl_feature2{j}(ind2,[ 1 2 3 end ]);
    image_match1 = [image_match1;Match1Tmp]; 
    image_match2 = [image_match2;Match2Tmp]; 
    end
end
close all;
%显示最后处理的效果
[LineCoordX,LineCoordY,N] = func_figure(img1s,image_match1,img2s,image_match2,Feature_point);

三、仿真测试结果

我们分别对三种不同情况进行讨论：

即平移，缩放和旋转情况进行讨论。

传统的SIFT原理就不做介绍了，

我们首先对传统的SIFT进行仿真，仿真效果如下所示：

缩放：

平移

旋转：

从上面的仿真结果可知，传统的SIFT，存在很多错误的匹配点，而且当旋转的时候，直接无法进行匹配识别了。

改进后的SIFT，我们考虑加入空间旋转，使得SIFT的性能得到提升：

缩放：

平移

旋转：

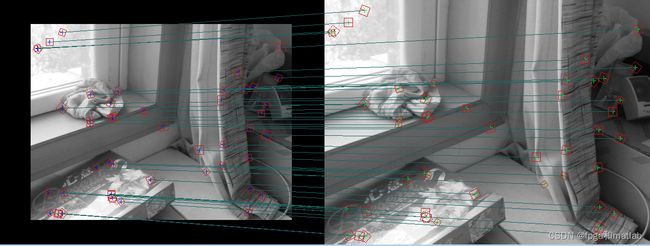
改进后的方法，可以对不同旋转角度的图像进行匹配，而且基本没有错误的匹配点：

A09-42