基于MATLAB的图像复原
基于MATLAB的图像复原系统
一、课题背景
随着信息技术的发展,数字图像像已经充斥着人们身边的任意一个角落。由于图像的传送、转换,或者其他原因,可能会造成图像的降质、模糊、变形、质量下降、失真或者其他情况的图像的受损。本设计就针对“图像受损”的问题,在MATLAB环境中实现了利用几何失真校正方法来恢复被损坏的图像。几何失真校正要处理的则是在处理的过程,由于成像系统的非线性,成像后的图像与原图像相比,会产生比例失调,甚至扭曲的图像。
图像复原从理论到实际的操作的实现,不仅能改善图片的视觉效果和保真程度,还有利于后续的图片处理,这对医疗摄像、文物复原、视频监控等领域都具有很重要的意义。
二、 图像复原的方法及其应用
2.1 图像复原的方法
在图像的获取、传输和保存的过程中,由于各种原因,如大气的湍流效应、传感器特性的非线性、成像设备与物体之间的相对运动、摄像设备中光学系统的衍射、胶片颗粒噪声和感光胶卷的非线性、光学系统的像差以及电视摄像扫描的非线性等所引起的几何失真,都可能造成图像的畸变和失真。通常,由于这些因素引起的质量下降称为图像退化[1]。
图像退化的表现是图像出现模糊、失真以及附加噪声等。由于图像的退化,在图像接收端显示的图像已经不再是发送的原始图像,图像的效果明显变差,因此我们可以采用一些技术手段来尽可能的减轻甚至消除图像质量的下降,还原图像的本来面目,这就是图像复原[2]。
图像复原是图像处理领域中一种非常重要的处理技术,与图像增强等其他基本图像处理技术类似,也是以获取视觉质量程度的改善为目的,所不一样的地方是图像复原过程实际上是一个估计的过程,需要根据一些特定的退化模型,对退化图像进行校正。简而言之,图像复原的处理过程就是提升退化图像的质量,并通过图像质量的提高来达到图像在视觉上的改善。
因为引起图像退化的原因很多,且性质各不相同,目前还没有统一的复原方法,许多研究人员根据不同的应用环境,采取了不同的退化模型[3-4]、估计准则和处理技巧,所以得到了各种复原方法。
图像复原的算法是整个技术的核心内容。目前,国内在这方面的研究才刚起步,而国外已经取得了较好的成果。早期的图像恢复是用光学的方法对失真的测试图像进行复原,但是关于数字图像复原技术的研究则是从对天文观测图像的后期处理中才逐渐发展起来的。其中一个成功例子是在1964年,NASA的喷气推进实验室用计算机处理有关月球的照片。照片是用电视摄像机在空间飞行器上拍摄的,图像的复原包括消除噪声和干扰等因素,校正几何失真和对比度损失以及反卷积。另一个典型的例子则是对肯尼迪遇刺事件现场照片的处理。由于事情发生的太突然,照片是在相机移动地过程中拍摄的。图像复原的主要目的就是消除移动造成的失真。还有其在在医学领域,图像复原的技术能广泛的应用于X光,CT,B超等成像系统,用来抑制各种医学成像系统或图像获取系统的噪声,改善医学图像的分辨率[5]。
现今的复原方法有:维纳滤波、逆滤波、最小二乘滤波、几何失真校正等多种复原方法。随着数信号处理和图像处理的发展,新的复原算法不断出现,不同的复原方法所需的条件是不相同的,所以在应用中可以根据具体情况加以选择。
2.2 图像复原的应用
目前国内外对于图像复原技术的研究和应用主要集中在空间探索、天文观测、物质研究、遥感遥测、军事科学、生物科学、医学影象、刑事侦察、交通监控等领域。如在生物方面,主要是用于生物活体细胞内部组织的三维再现和重构,通过复原荧光显微镜所收集的细胞内部的逐层切片图,来重现细胞内部构成;医学方面,如对肿瘤周围组织进行显微观察,以获取肿瘤安全切缘与癌肿原先部位之间关系的定量数据;天文方面则采用迭代盲反卷积进行气动光学效应图像复原研究等。
三 几何失真校正实现
在图像的获取或者显示的过程中通常会产生几何失真,比如成像系统有一定的几何非线性,其主要原因是视像管摄像机和阴极射线管显示器的扫描偏转系统有一定的非线性,所以会造成图像的枕形失真或桶性失真。另外,由卫星拍摄的地球表面的图像往将往覆盖较大的面积,由于地球表面呈球形,这样拍摄的图像同样会有比较大的几何失真。
几何失真一般分为系统失真和非线性失真。系统失真是有规律的、能预测的;而非线性系统的失真则是随机的。当对图像进行定量分析的时候,就要先对畸变的图像进行准确的几何失真校正[12](即把几何失真的图像校正成与原图像相差无几的图像),以免影响分析精度。基本的方法是:首先,要建立几何校正的数学模型;其次,用已知的条件来确定模型参数;最后,根据畸变模型对图像进行几何校正。通常可以分为以下两步:
(1)图像空间坐标的变换;
(2)确定校正空间各像素的灰度值(灰度内插)。
3.1 空间变换
假设一幅图像为,经过几何失真变成了,其中,表示的是失真图像的坐标,而不是原图像的坐标。上述变化可表示为:
(3-1)
(3-2)
这里,和是空间变换,产生了几何失真图像。
若函数和已知,则可以依据一个坐标系统的像素坐标算出另一坐标系统的对应像素的坐标。在已知情况下,通常和可用多项式来近似:
(3-3)
(3-4)
式中,为多项式的次数,和为各项系数。
3.1.1 已知和条件下的几何校正
若我们具备先验知识、,则希望将几何畸变图像恢复为基准几何坐标的图像。几何校正通常分为直接和间接两种方法。
- 直接法。先通过来推出,然后计算每个像素的校正坐标值,保持各像素灰度值不变,然后生成一幅校正图像,但其像素的分布是不太规则的,可能会出现疏密不均、像素挤压等现象。
- 间接法。假设复原图像的像素在基准坐标系统内是等距网格的交叉点,从网格交叉点的坐标出发,可以算出在已知几何畸变图像上的坐标,即:
(3-5)
虽然点坐标为整数,但一般不为整数,不会刚好就处于畸变图像像素的中心,所以不能直接明确该点的灰度值,而只能由其在几何失真图像的周围像素灰度内插求出,作为对应像素的灰度值,据此可以获得校正之后的图像。由于间接法内插灰度比较容易,所以在通常情况下采用的是间接法来进行几何失真校正。
3.1.2 和未知条件下的几何失真
在这种情况下,通常用原始图像和几何畸变图像上多对“连接点”的坐标来确定和。
假设基准图像像素的空间坐标和待校正图像的对应像素的空间坐标之间的关系用二元多项式来表示,表达式如下:
(3-6)
(3-7)
式中,为多项式的次数,和为各项待定系数。
对于线性失真:
(3-8)
(3-9)
对于一般的(非线性)二次失真:
(3-10)
(3-11)
利用“连接点”建立失真图像与校正图像之间其他像素空间位置的相应关系,而“连接点”在失真图像和校正图像中的位置是精确已知的。失真图像和校正图像中有四边形区域,这两个四边形的顶点就是相应的“连接点”。假定四边形区域中的几何畸变的过程可以用二次失真方程来表示,即:
(3-12)
(3-13)
将以上两个表达式代入式(3-1)和式(3-2)中,得:
(3-14)
(3-15)
因为一共有四对“连接点”,代入式(3-14)和式(3-15)可得8个联立方程,由这些方程可以解出8个系数、、、、、、、。这些系数就可以形成用于变换四边形区域内所有像素的几何失真模型,即空间映射公式。通常来说,可以把一幅图像分割成一系列覆盖全图的四边形区域的集合,在每个区域寻找足够的“连接点”用来计算进行映射所需的系数。
只要有了系数,校正(即复原)图像就不那么困难了。如果想找到非线性失真图像在任一点的的值,需要简单地知道在失真图像中的什么地方被映射。为此,可以把代入式(3-14)和式(3-15)得到几何失真坐标。在无失真图像中被映射到点的值是。这样简单地令,就得到了复原图像的值。
3.2 灰度插值
最简单的灰度灰度插值是最近邻插值(也称为零阶插值),该方法实现起来相对简单,但是有时不够精确,甚至经常产生不希望的认为疵点,如高分辨率图像直边的扭曲;对于通常的图像处理,双线性插值很实用;更完善的技术如样条插值、立方卷积内插等可以得到较平滑的结果,但是更平滑的仿真的代价就是增加计算开销。
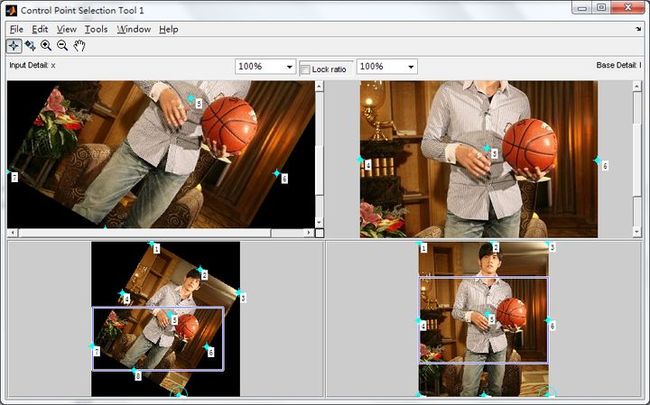
在MATLAB[13]软件中生成如图3.1所示的figure图像,然后在figure图像上的失真图像和原始图像上选取九对点,最后依据选取的九对点来进行校正。
图3.1 选取连接点图像
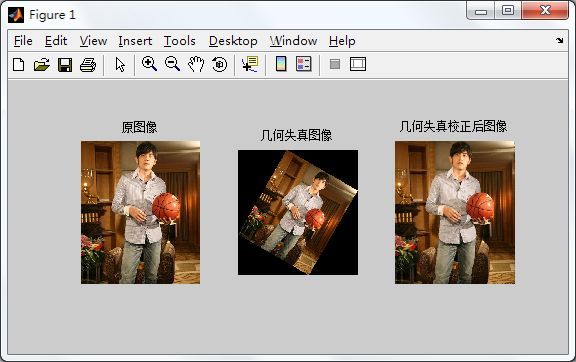
图3.2 几何失真及校正后图像
3.3 结果分析
图3.1是调用cpselect函数,使系统启动交互连接点工具,然后在figure文件上的图像交替选择对应的坐标点,将其输出到Workspace中,进行坐标点的统计;图3.2是校正的结果,第二张是几何失真之后的图像,第三张是几何校正后的图像,校正后的图像和原图像相比,几乎没有什么差别,所以几何失真校正复原出来的结果很好,但是它的适用条件是图像的几何失真,其他的失真方式,比如说图像的质量退化,就不可以采用这种复原方法。
四、参考文献
[1] 朱冠南.基于MATLAB的图像复原设计[J].技术交流,2019:87.
[2] 王婷.退化图像的复原改进算法研究与实现[D].哈尔滨:哈尔滨工程大学,2017.
[3] 何东健.数字图像处理[M].西安:西安电子科技大学出版社,2013:263-264.
[4] 胡学龙,许开宇.数字图像处理[M].北京:电子工业出版社,2016:111-132.
[5] 吴亚东.图像复原算法研究[D].成都:电子科技大学,2016.
[6] 杨杰.数字图像处理及MATLAB实现[M].北京:电子工业出版社,2013:127-131.
[7] Rafael C Gonzalez,Richard E Woods,Steven L Eddins.Digital image processing(MATLAB)[M].Addison-Weslwy, Publishing Company Inc. New York, 1993:189-207.
五、参考代码
几何失真校正9对连接点的选取代码:
I=imread('F:\素材\2.jpg');
theta=pi/6; %变换旋转角度
T=[cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0;0 0 1]; %变换矩阵
tform1=maketform('affine',T); %几何变换结构
x=imtransform(I,tform1,'nearest'); %以最近邻插值进行仿射变换
F=cpselect(x,I); %调用cpselect函数来启动交互选择连接点工具
几何失真校正代码如下所示:
I=imread('F:\素材\2.jpg');
subplot(131);
imshow(I);
title('原图像');
k=0.7;
theta=pi/6;
T=[k*cos(theta) k*sin(theta) 0;-k*sin(theta) k*cos(theta) 0;0 0 1];
tform1=maketform('affine',T);
x=imtransform(I,tform1,'nearest');
subplot(132);
imshow(x);
title('最近邻插值的放射变换');
base_points=[1.7500 1.2500;188.2500 2.7500;332.7500 1.2500;327.7500 194.7500;177.7500 189.2500;2.7500 200.7500;2.7500 396.2500;166.2500 396.2500;331.2500 394.2500]; %从原始图像I中选择的9个连接点的坐标矩阵
input_points=[200.9787 3.1263;360.0565 96.1718;486.1182 168.2070;389.3209 336.2898;257.2562 255.2496;103.4310 174.2100;4.3825 346.0441;144.7012 424.0822;288.0213 508.1233]; %从几何失真图像x中选择的9个连接点的坐标矩阵
tform=cp2tform(input_points,base_points,'affine'); %由9对连接点坐标矩阵建立几何变换结构
F=imtransform(x,tform,'XData',[1 333],'YData',[1 398]);
subplot(133);
imshow(F);
title('几何失真校正');