通俗易懂的 k-means 聚类算法原理及优化（附代码）

  K-means算法的基本思想是：以空间中个点为中心进行聚类，对最靠近他们的对象归类。通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果。

1、算法步骤

  输入：聚类个数，以及包含个数据对象的数据集
  输出：满足方差最小标准的个聚类
  Step1 从个数据对象任意选择个对象作为初始聚类中心；
  Step2 根据簇中对象的平均值，将每个对象重新赋给最类似的簇；
  Step3 更新簇的平均值，即计算每个簇中对象的平均值；
  Step4 循环Step2到Step3直到每个聚类不再发生变化为止。

2、详细过程

  1) 给定大小为 $n$ 的数据集，令 $iter=1$，表示迭代次数，选择 $k$ 个初始聚类中心 $z_j(iter),j=1,2,\dots ,k$ ；
  2) 计算每个样本数据 $x_i,i=1,2,\dots ,n$ 与聚类中心的距离，将 $x_i$ 分配给最近的聚类中心 $z_j(iter)$ 所属的聚类，即 $|x_i-z_j(iter)|\le |x_i-z_{j^{{}^{\prime }}}(iter)|,j^{{}^{\prime }}\ne j,j^{{}^{\prime }},j\in (1,2,\dots .k)$；
  3) 令 $iter=iter+1$，计算新的聚类中心（取已聚类的平均值）和误差平方和准则 $F$ （目标函数）值
$$F(iter)=\sum _{j=1}^k\sum _{i=1}^n\Vert x_i^j-z_j(iter){\Vert }^2$$
  4) 判断：若 $|F(iter+1)-F(iter)|<\theta$ （$F$ 收敛） 或者对象无类别变化，则算法结束，否则，返回第 2）步。

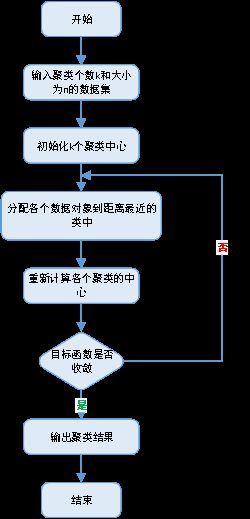
3、流程图

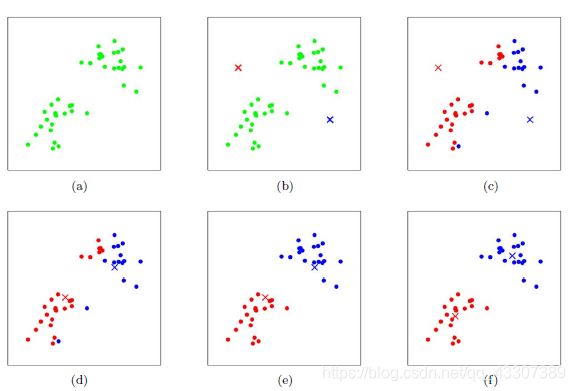
4、聚类过程示意图

（和测试效果图无关，只是为了展示）

5、测试效果

6、算法优化

   由于随机聚类中心的不同，在最小化代价函数时，有可能会停留在一个局部最小值处，导致最终的聚类效果不佳。需要对初始化质心点的选择进行优化。
   优化：选择批次距离尽可能远的 $k$ 个点（事先确定的类簇个数），首先随机选择一个点作为第一个初始类簇中心点，然后选择距离该点最远的那个点作为第二个初始类簇中心点，然后再选择距离前两个点的最近距离最大的点作为第三个初始类簇的中心点，以此类推，直至选出 $k$ 个初始类簇中心点。
   下面是优化后初始质心点选择的代码部分（所用语言C#）：

DataPoint firstCenterPoint = new DataPoint(dataSet[0].X, dataSet[0].Y, 1); //选择第一个点作为第一个随机点
int n = 2;
centerPoints.Add(firstCenterPoint);
for (int i = 0; i < k - 1; ++i, ++n)
{
	List<double> tempList = new List<double>();
	for (int j = 0; j < len; ++j)
	{
		bool brFlag = false;
		for (int m = 0; m < centerPoints.Count(); ++m)
		{
			if (dataSet[j].X == centerPoints[m].X && dataSet[j].Y == centerPoints[m].Y)
			{
			brFlag = true;
			break;
			}
		}	
		if (brFlag)
		{
			tempList.Add(0);
			continue;
		}

		List<double> ceterPointSd = new List<double>();
		for (int m = 0; m < centerPoints.Count(); ++m)
		{
			double tempSd = Math.Sqrt(SquareDistance(dataSet[j], centerPoints[m]));
			ceterPointSd.Add(tempSd);
		}
		double minSd = ceterPointSd.Min();
		tempList.Add(minSd);
	}
		
	int maxIndexValue = tempList.Select((m, index) => new { m, index }).Where(x => x.m == tempList.Max()).FirstOrDefault().index;
	DataPoint centerPoint = new DataPoint(dataSet[maxIndexValue].X, dataSet[maxIndexValue].Y, n);
	centerPoints.Add(centerPoint);
}