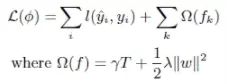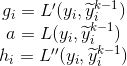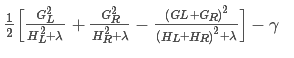集成学习之Xgboost超详细推导
前言
继上篇GBDT的介绍集成学习之GBDT超详细推导_爱吃火锅的博客-CSDN博客_gbdt推导
我们来看看其升级版，也是目前用的比较多的Xgboost模型，建议先看上篇博客，再来看本篇会容易些
当然了也希望去看一下集成学习这一大家族的整体框架机器学习之集成学习_爱吃火锅的博客-CSDN博客
相信会有一个整体宏观的把握
为了统一化，衔接化，本文还是采用与之前介绍GBDT那样的思路进行介绍，但是每一部分会采用“相同点，不同点”即与GBDT对比的方式进行介绍，当然了，有了前篇文章的铺垫，这里着重介绍不同点，相同点一笔带过，如有疑问，翻看前篇，不在累述。
最后也会介绍一下Xgboost所特有的功能以及关于其的两个实践
当然了,有时间最好还是拜读一下原论文吧，毕竟这是最权威的啦：
https://arxiv.org/pdf/1603.02754v1.pdf
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
DT决策树
相同点：
本质都是回归树
不同点：
1）采用的基学习器不但是CART，而且可以是线性分类器，但是一般来说采用决策树的结果往往比较好，所以还是采用决策树的时候多一些，这也是为什么在一些比赛或者项目中使用xgboost模型的时候将booster这个超参数设为gbtree原因，当然其也是默认值
2）在构建树寻找最佳分割点的时候采用的标准不再试最小化均方差，而是采用了与损失函数相关的增益最大化，对比来看，GBDT采用的标准其实是一种启发式的，不管我们选用什么样的损失函数，但是其采用的标准都不变即总是最小化均方差，从该角度来看 貌似和损失函数都没有联系，显然这是不好的，于是乎，Xgboost弃用了这一点，而是采用了直接和损失函数有联系的方式进行划 分，至于怎么具体划分，我们会在结合GB来一起看，请往下看。
总结来说就是：首先GBDT是每一个基分类器去拟合前K个基学习器的一阶导数，采用的损失函数多种多样（Log Loss也好，softmax Loss也好），构造树这一过程采用的准则就是均方误差，分开看这两部分，前一部分采用的损失函数是为了衡量前K个基学习器线性组合好后这一整体的性能，第二部分的损失函数是为了衡量当前训练这一棵树（即第K+1颗树）的性能，GBDT某种程度上来讲独立了两部分，即不管前一部分采用什么损失函数，在训练当前这一棵树的时候都是采用最小化均方差（当然也可以是别的，但GBDT就是用来MSE这一损失函数），显然这没有联系，是不好的，于是乎Xgboost将两部分采用的损失函数联系了起来，即Xgboost建单个树采用的损失函数和第一部分是有联系的，不再拘泥于均小误差，抽象出各种损失函数一个表达式。最小之，进而才有了接下来的一推公式，可以说这是出发点。
---------------------------------------------------------------------------------------------------------------------------------------------------------------------
GB梯度提升
相同点：
还是采用了boosting的思想，即当前基学习器是根据前面基学习器学习得来的，而且利用的信息是梯度
不同点：
其实可以总结为两点：
1）目标函数不再像GBDT那样单纯的是损失函数，Xgboost的目标函数是损失函数+正则项
目的就是通过正则项来控制模型的复杂度
2）Xgboost不仅利用了一阶导数信息而且还利用了二阶导数的信息，而GBDT仅仅利用了一阶导数的信息。
目的就是为了配合我们在构造树划分节点时采用了和损失函数有直接联系的新标准的使用。
牢牢把握住上面两个方法或者说出发点，我们来完整看一下其过程：
首先目标函数变为：
注意在GBDT中是没有
这一正则项的。
参数说明：
L：损失函数
T：叶子节点个数
W:叶子节点的输出值
：正则项参数
:和GBDT中的含义有些不同，这里的其实并不是前k个基学习器的输出值累加和，而是当前基学习器的输出值，类似 GBDT中h(x)，而GBDT中的其实在这里的表达式是
即
所以目标函数其实可以写为：
到目前为止第一个出发点解决了很简单就是后面加了个正则项，其它和GBDT没有任何不同，无非在数学表达上换了几个字母而已，本质没变。
下面就是第二个出发点，也是Xgboost与GBDT的最大不同及优势所在。
将目标函数泰勒展开：
这里可能有点难理解，其实对比一下泰勒展开公式便一目了然：
注意看目标函数经过泰勒展开后公式形式，看似复杂，实在简单的很，别被其表象迷惑：其中
都是常数，为什么呢？很简单，假设损失函数模型采用了一种，不论是对其求一阶导数还是二阶导数，其结果必定是含有的数学表达式，而都是常数，所以上面三个表达式都是常数，记
则原目标函数表达式为：
![\begin{matrix} \sum _{i}[L(y_{i},\widetilde{y}^{k-1}_{i})+{L}'(y_{i},\widetilde{y}^{k-1}_{i})f_{k}(x)+\frac{1}{2}{L}''(y_{i},\widetilde{y}^{k-1}_{i})f^{2}_{k}(x)]+\sum _{k}\Omega (f_{k}(x))\\ =\sum _{i}[a+g_{i}f_{k}(x)+\frac{1}{2}h_{i}f^{2}_{k}(x)]+\frac{1}{2}\lambda \sum_{j=1}^{T}\left \| w_{j} \right\|_{2}+\gamma T\end{matrix}](http://img.e-com-net.com/image/info8/f6fb272cda4345f78e425576d35f383c.gif){kind=small}
进一步化简：
注意这其实就是一个简单的以为变量的二次函数，现在我们要求其最小值，这也是我们构造树分裂节点时所采用的标准
二次函数怎么求最值呢.很简单了吧，求导令其为0即可：
首先令
对求导令其为0可得：
将其带入目标函数可得：
现在我们看这个公式中的：
其在一定程度上就代表了当前目标函数的最小值对吧，那么我们在构造树分裂节点的依据标准是使得目标函数最少，那我们可以这样想：假设没有分裂前目标函数的最小值是X1,分裂后统计所有叶子节点的目标函数总值为X2,要的结果就是X1-X2越大越好是吧，即增益越大越好，具体到这里就是：
公式中L，R代表的分别是左右。
考虑到正则项，增益应该是：
即增益只有大于时才会考虑分裂，也就是说当小于时，就不分裂了，树的深度就不会再增加，所以说其是控制数复杂度的一个参数，即在使用模型时有一个超参数gamma需要设置，该值默认是0，在节点分裂时，只有在分裂后损失函数的值下降了，才会分裂这个节点。Gamma指定了节点分裂所需的最小损失函数下降值。这个参数值越大，算法越保守。
顺便这里说一下，使用模型时对应的就是lambda默认是1，我们这里使用的是L2正则项，当使用的是L1正则项时对应的便是alpha。
注意两个参数作用都是防止过拟合。
有了上面的计算方法就会构建树就很简单了，无非就是遍历每一个特征，然后在每一个特征下在遍历每一个值，看看究竟谁的增益值最大，最后就可以选取该特征且对应的分裂值。
同时需要注意的一点就是我们实际在使用xgboost模型的时候有一个超参数min_child_weight，它的作用是：
min_child_weight<
即左右子树区域的二阶导数的和值都必须大于min_child_weight
假设当前的特征对应的分裂值的增益是最大的，但是其不满足上述，那么模型是不会采用该分裂值作为分裂节点的，而是会考虑次增益是最大的裂值，同理也要检查是否满足上述约束。
那么叶子节点的输出值是什么？那就是
。
最后整体看一下其算法过程：
先看算法一：(牢记g,G是一阶导数，G是树划分后某一个叶子区域所有g的和，h,H是二阶导数，H是树划分后某一个叶子区域所有h的和)
初始化：一般是将第一步的预测，当然这里可以设置为其它值，对应模型中的就是base_score参数设置，经验值是正样 本数目/整体样本数，其实当训练的轮数足够多，也就是说基学习器足够多的时候，该值对结果影响并不会太大，只不 过 根据刚才的经验值设置，一般来说收敛会快些。
然后根据损失函数可以求得一阶导数和二阶导数，将代入就可以得到每一个样本的
接下来是分裂点选取过程：
遍历每一个特征（图片中的第一个for），遍历该特征下的每一个可能分裂值（图片中的第二个for）
通过上面可以将样本分到两边，然后根据每个叶子区域下包含的样本就可以得到每个叶子区域下的
假设经过分裂后左树中包含的样本是1,4,7，这三个样本的一阶导数分别是2,3,5二阶导数分别是1,3，6那么
有了
,便可以计算当前的增益即图片中的score
最后循环结束，选取能够使得score最大的特征以及其分裂值作为当前该树的分裂节点，如果树的深度很大，可以在此基础上接着往下分裂，过程和上面是一样的，直到不能不分为止，即增益不变为0，当然如果设置了gamma，那就是直到增益等于gamma停止。
树的分裂节点通过上面可以选出来，树的输出值也通过
可以得到，至此当前这颗树就算训练好了！！！！！！！！！！！
接下来就是训练下一棵树，比如该训练第八棵树了，那么此时的是多少呢？
那就是j将样本i带到第六棵树中，看其输出是多少，那么就是多少，如此知道了和
，便又可以计算当前每个样本的，后面又是构建树的过程，和上面一样，这里不再累述。
所以可以看到图片中给出的其实是一棵树的构造过程，而并不是整个Xgboost算法的过程，如果要完整的Xgboost算法的过程其实外层还得有个for循环即一共构造多少棵树。
再来看算法二：算法一是使用exact greedy算法来寻找分割点建树，但是当数据量非常大难以被全部加载进内存时，那么该算法便不再适合，于是算法二就是对这一块的优化。
假设对于某一个特征,算法会根据特征分布的分位数找到切割点的候选集合（对应算法二中的第一个for），即
然后遍历这些点，使其分别作为该特征下的分裂值，然后就是利用我们在算法一种介绍的方法，计算出G和H，接着依次计算增益
对比就可以得到该特征值的最佳分裂值。
有两种近似算法：一种是全局算法，即在初始化tree的时候划分好候选分割点，并且在树的每一层都使用这些候选分割点；另一种是局部算法，即每一次划分的时候都重新计算候选分割点。这两者各有利弊，全局算法不需要多次计算候选节点，但需要一次获取较多的候选节点供后续树生长使用，而局部算法一次获取的候选节点较少，可以在分支过程中不断改善，即适用于生长更深的树。
算法二的难点其实就在于第一个for，有了第一个for，第二for那就是遍历特征，而且每个特征下的候选分裂值都有了，直接计算增益对比就行。
总结一下：
第一个for就是找每一个特征下的候选分裂值集合，而这也是算法二的最核心东西。
第二个for就是遍历特征，利用第一个for得到的每一个特征下的分裂值去得到最佳分裂节点，这部分和算法一的过程一模一样，不再累述。
那么截止目前，待解决问题就剩下第一个for了，那它采取的到底是什么神秘算法呢？那就是Weighted Quantile Sketch。
关于Weighted Quantile Sketch是一个很大的分支问题，介绍起来也需要很大篇幅，本文重在就讲xgboost原理，算法二的该部分其实算作是优化了吧，所以这里就仅仅简单介绍一下算法二，给出它的背景和目的，想要更多了解算法二，尤其是Weighted Quantile Sketch大家可以自行查阅资料，笔者也在不断学习过程，有懂得大家可以彼此交流一下，这里推荐一篇这方面的博客吧：Xgboost近似分位数算法_anshuai_aw1的博客-CSDN博客
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Shrinkage
这部分其实和GBDT是一样的实际中并不会直接
而是在会有一个系数其值介于0和1之间，目的就是我们在GBDT所说的是每一步的步伐小一点，进而可以尽最大可能逼近最优解，当然它是以收敛速度作为代价的。
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
Xgboost训练过程总结：
初始化
将带入损失函数的求导结果中，计算得到,遍历特征得到,根据最大增益选出分裂节点。
计算得到树的输出值
训练第二课树，将输入到第一棵树，得到输出值即得到
，有了计算得到,遍历特征得到,根据最大增益选出分裂节点。
计算得到树的输出值
训练第三课树，将输入到第二棵树，得到输出值即得到
，有了计算得到,遍历特征得到,根据最大增益选出分裂节点。
计算得到树的输出值
.........................................
.....................................
结束
-----------------------------------------------------------------------------------------------------------------------------------------------------------
Xgboost选取特征
在训练完后，可以通过get_fscore()来选用特征其有三个参数
‘weight’ - the number of times a feature is used to split the data across all trees.
‘gain’ - the average gain of the feature when it is used in trees.
‘cover’ - the average coverage of the feature when it is used in trees.
首先看‘weight’，它的最后效果就是如下图会输出每个特征的重要程度
图片来源：转：xgboost特征选择_纸上得来终觉浅-CSDN博客
可以看到cont7这个特征是比较重要的，那么它是通过什么来衡量特征的重要性呢？很简单，那就是在我们Xgboost训练的过程中其会记录下每一个特征被用来当做划分节点的次数有多少次，假如我们一共训练了三棵树，第一棵树特征x被用了2次，第一棵树特征x被用了3次,第一棵树特征x被用了1次.那么我们统计的时候就是x一共被用了2+3+1=6次，其它特征值依次类推，最后我们看的是谁被用的次数多谁就重要性高。
‘gain’是每个特征的平均增益，还是假设X1特征一共被选用了6次来作为分裂节点，依据我们上面介绍的方法计算出处其每次的增益分别是：1.2,3,5,6,4,7,那么该特征的平均增益就是（1.2+3+5+6+4+7）/6=4.5，同理该值越大，代表的该特征值越重要。
‘cover’是每个特征的平均二阶导数，还是假设X1特征被用了6次，假设样本是4个，先看第一次的时候我们肯定会遍历X1特征下的所有备用分裂值，每遍历一个就会得到一个,假设备用值一共有7个，那么就是得到7个，所以第一次的时候就是会得到14个数，记录下来，然后假设第二次我们又记录了10个值，依次类推，最后6次记录玩了以后，假设一共是50个数，那么这50个数的平均值就是‘cover’，其所代表的含义就是所涵盖的样本的数量
-----------------------------------------------------------------------------------------------------------------------------------------------------------
Xgboost可处理缺省值
GBDT是不能处理缺省值的，这样来看Xgboost又有一大优点是吧
那它是怎么来处理缺省值的呢？请看其算法：
可以看到，这里相比算法一内部多了一个for
代表的就是当前特征下备选的分类值集合，可以想象其是具体的一个一个的值，是没有缺省值的，而G中是整体的集合即其包含缺省值，所以对于第一个for来说左树时没有缺省值的，而右树含有缺省值（总样本的集合减去左树的样本），而第二个恰好反过来，右树是没有缺省值的，左树是有缺省值的，最后看两种分法那种增益高，就选哪个。
这样说可能有点抽象，我们还是来举个例子：
假设现在一共4个样本，我们现在选用的特征是x1，这四个样本在x1的特征值分别是1,2，NAN,5即第三个样本是缺省值。
假设我们现在要训练第5棵树，那么我们将这是个样本输入输入到第4棵树中，看其输出值即求
样本0,1,3都是有值的，输入到树中，最后肯定能落在某一叶子节点，相应的也有一个输出值即可求出，那么2这个样本呢？第一次我们就先假设它落在右子树，将右子树对应的输出值作为
,
这样就可以算出一个增益，整个过程就是第一个for
然后我们第二次假设其落在左子树，将左子树对应的输出值作为,也就是第二个for
注意两次for过程其实是不变的。
最后看看两种情况哪种增益高就将样本2划到哪边。
总结一下就是：
将缺省值分别划到左右两面试一试，看看哪个更好？优中选优！！！！！！！
--------------------------------------------------------------------------------------------------------------------------------------------------------------
Xgboost和GBDT的不同与联系：
相同点：
1）都是采用了boosting这一提升学习的思想。
2）都是例如了梯度这一信息变量
不同点：
1）Xgboost加入了正则项，即是损失函数+正则项，而GBDT只有损失项，Xgboost可以灵活的控制模型的复杂大，相比GBDT做了更多的过拟合控制。
2）GBDT在构造树的时候是采用了最小化均方差这一启发式准则，而无视了具体的损失函数是什么，Xgboost是采用了最大化增益，即最小化目标函数，即最小化具体使用的损失函数最为准则，进而导致GBDT只是利用了一阶导数，而Xgboost利用一阶导数，二阶导数的信息
3）Xgboost能够自动处理缺省值，而GBDT不可以
------------------------------------------------------------------------------------------------------------------------------------------------------
Xgboost实践：
实践一：另一篇博客：Xgboost实践+第一名天池o2o优惠券的使用预测思路完整版_爱吃火锅的博客-CSDN博客_o2o优惠券使用预测第一名
是关于天池上面的一个比赛
实践二：Xgboost 实践：基于收支记录判断借贷意愿_爱吃火锅的博客-CSDN博客
比Xgboost更快的LightGBM:LightGBM源码阅读+理论分析（处理特征类别，缺省值的实现细节）_爱吃火锅的博客-CSDN博客_lightgbm源码
看到很多小伙伴私信和关注，为了不迷路，欢迎大家关注笔者的微信公众号，会定期发一些关于NLP的干活总结和实践心得，当然别的方向也会发，一起学习：
