深度学习:优化方法——momentum、Nesterov Momentum、AdaGrad、Adadelta、RMSprop、Adam
深度学习:优化方法
-
-
- 1. 指数加权平均(Exponentially weighted average)
- 2. 带偏差修正的指数加权平均(bias correction in exponentially weighted average)
- 3. 动量(momentum)
- 4. Nesterov Momentum
- 5.AdaGrad(Adaptive Gradient)
- 6. Adadelta
- 7.RMSprop(root mean square prop)
- 8.Adam(Adaptive Moment Estimation)
- 8. 该如何选择优化算法
-
1. 指数加权平均(Exponentially weighted average)
指数加权平均是处理时间序列的常用工具,下面用一个例子来引入指数加权平均的概念。下图是一个180天的气温图(图片来自ng Coursera deep learning 课):

如果我们想找一条线去拟合这个数据,该怎么去做呢。我们知道某一天的气温其实和前几天(前一段时间)相关的,并不是一个独立的随机事件,比如夏天气温都会普遍偏高些,冬天气温普遍都会低一些。我们用[θ1、θ2、…、θn]表示第1,2,…,n天的气温,我们有:
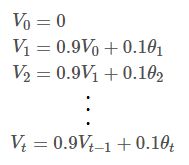
下面来正式的看一下 指数加权平均(Exponentially weighted average) 的定义
![]()
可以认为 V t V_t Vt近似是 1 1 − β \frac{1}{1−β} 1−β1天的平均气温,所以上面公式设置了β=0.9,当 t>10 时,则可以认为 V t V_t Vt近似是它前10天的平均气温。 比如,按照上面的公式,我们计算 V 100 V_{100} V100
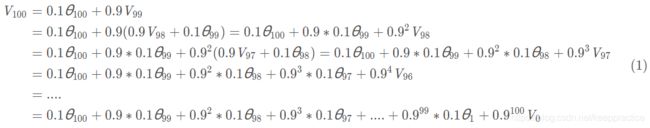
从上面的公式能够看出,实际上是个指数衰减函数。 0. 9 10 ≈ 0.35 ≈ 1 e 0.9^{10}≈0.35≈ \frac{1}{e} 0.910≈0.35≈e1,所以这个就解释了上面的 1 1 − β \frac{1}{1−β} 1−β1
下面再看下 β β β 取不同值时,曲线的拟合情况(图片来自ng deep learning课)

从上图能够看出:
当 β \beta β 较大时( β = 0.98 \beta = 0.98 β=0.98 相当于每一点前50天的平均气温),曲线波动相对较小更加平滑(绿色曲线),因为对很多天的气温做了平均处理,正因为如此,曲线还会右移。
同理,当 β \beta β 较小时( β = 0.5 \beta = 0.5 β=0.5 相当于每一点前2天的平均气温),曲线波动相对激烈,但是它可以更快的适应温度的变化。
关于指数加权平均的优缺点: 当 β = 0.9 \beta = 0.9 β=0.9 时,我们可以近似的认为当前的数值是过去10天的平均值,但是显然如果我们直接计算过去10天的平均值,要比用指数加权平均来的更加准确。但是如果直接计算过去10天的平均值,我们要存储过去10天的数值,而加权平均只要存储 V t − 1 V_{t-1} Vt−1
2. 带偏差修正的指数加权平均(bias correction in exponentially weighted average)
上一节中介绍了指数加权平均,用的公式是:
![]()
当我们令β=0.98时,我们想得到下图中的“绿线”,实际上我们得到的是下图中的“紫线”。对比这两条线,能够发现在“紫线”的起点相比“绿线”非常的低,举个例子,如果第一天的温度是40℃,按照上面的公式计算 V 1 = 0.98 V 0 + ( 1 − 0.98 ) θ 1 = 0.98 ∗ 0 + 0.02 ∗ 40 = 0.8 V_1=0.98V_0 +(1−0.98)θ_1 =0.98∗0+0.02∗40=0.8 V1=0.98V0+(1−0.98)θ1=0.98∗0+0.02∗40=0.8,按照这个公式预估第一天的温度是0.8℃,显然距离40℃,差距非常大。同样,继续计算,第二天的温度也没有很好的拟合,也就是说 指数加权平均 不能很好地拟合前几天的数据,因此需要 偏差修正,解决办法就是,再令 V t = V t 1 − β t V_t=\frac{Vt}{1−β^t} Vt=1−βtVt因此, 带偏差修正的指数加权平均(bias correction in exponentially weighted average) 公式为:

再来按照上述公式对前两天温度进行计算, V 1 = V 1 1 − β t = 0.8 1 − 0.98 = 40 V_1=\frac{V_1}{1−β^t}=\frac{0.8}{1-0.98}=40 V1=1−βtV1=1−0.980.8=40,能够发现温度没有偏差。并且当 t → ∞ t\rightarrow \infty t→∞ 时, β t → 0 β^t→0 βt→0,这样在后期 V t V_t Vt就和 没有修正的指数加权平均一样了。

在机器学习中,多数的指数加权平均运算并不会使用偏差修正。因为大多数人更愿意在初始阶段,用一个捎带偏差的值进行运算。不过,如果在初试阶段就开始考虑偏差,指数加权移动均值仍处于预热阶段,偏差修正可以做出更好的估计。
3. 动量(momentum)
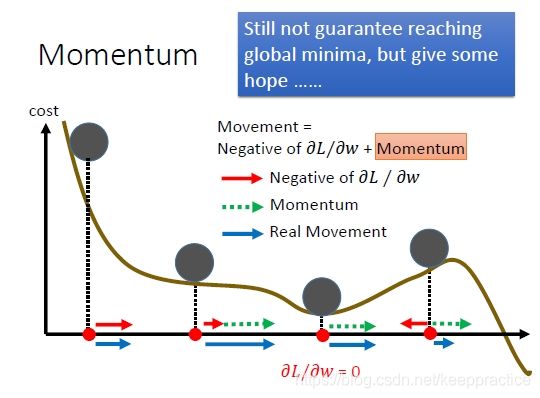
我们使用SGD(stochastic mini-batch gradient descent,深度学习中一般称之为SGD)训练参数时,有时候会下降的非常慢,并且可能会陷入到局部最小值中,如下图所示(图片来自李宏毅《一天搞懂深度学习》)。

动量的引入就是为了加快学习过程,特别是对于高曲率、小但一致的梯度,或者噪声比较大的梯度能够很好的加快学习过程。动量的主要思想是积累了之前梯度指数级衰减的移动平均(前面的指数加权平均),下面用一个图来对比下,SGD和动量的区别:

区别: SGD每次都会在当前位置上沿着负梯度方向更新(下降,沿着正梯度则为上升),并不考虑之前的方向梯度大小等等。而动量(moment)通过引入一个新的变量 vvv 去积累之前的梯度(通过指数衰减平均得到),得到加速学习过程的目的。
最直观的理解就是,若当前的梯度方向与累积的历史梯度方向一致,则当前的梯度会被加强,从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致,则会减弱当前下降的梯度幅度。
一个图来形象的说明下上面这段话(图片来自李宏毅《一天搞懂深度学习》):
下面给出动量(momentum)的公式:

β \beta β的值越大,则之前的梯度对现在的方向影响越大。 β \beta β一般取值为0.5, 0.9, 0.99。ng推荐取值0.9。这个公式是ng的在Coursera课上给出的。
关于这个公式目前主要有两种形式,一种是原论文里的公式:(原论文:On the importance of initialization and momentum in deep learning)

使用这个公式的有:
1、 goodfellow和bengio的《deep learning》书:(8.3.2节 momentum)

4. Nesterov Momentum
Nesterov Momentum是对Momentum的改进,可以理解为nesterov动量在标准动量方法中添加了一个校正因子。用一张图来形象的对比下momentum和nesterov momentum的区别(图片来自:http://ttic.uchicago.edu/~shubhendu/Pages/Files/Lecture6_pauses.pdf):

根据Sutskever et al (2013)的论文(On the importance of initialization and momentum in deep learning),nesterov momentum的公式如下:

goodfellow et al 的《deep learning》书中给的nesterov momentum算法:

和momentum的唯一区别就是多了一步红色框框起来的步骤。
但是,我们仔细观察这个算法,你会发现一个很大的缺点,这个算法会导致运行速度巨慢无比,因为这个算法每次都要计算 ∇ θ ∑ i L ( f ( x ( i ) ; θ + α v ) , y ( i ) ) \nabla_\theta\sum_iL(f(x^{(i)};\theta + \alpha v),y^{(i)}) ∇θ∑iL(f(x(i);θ+αv),y(i)),这个相当于又要把fp、bp走一遍。 $这样就导致这个算法的运行速度比momentum要慢两倍,因此在实际实现过程中几乎没人直接用这个算法,而都是采用了变形版本。
5.AdaGrad(Adaptive Gradient)
通常,我们在每一次更新参数时,对于所有的参数使用相同的学习率。而AdaGrad算法的思想是:每一次更新参数时(一次迭代),不同的参数使用不同的学习率。AdaGrad 的公式为
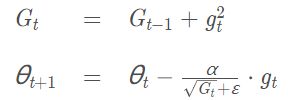
从公式中我们能够发现:
优点:对于梯度较大的参数, G t G_t Gt 相对较大,则 α G t + ε \frac{\alpha }{\sqrt{G_t }+ \varepsilon } Gt+εα 较小,意味着学习率会变得较小。而对于梯度较小的参数,则效果相反。这样就可以使得参数在平缓的地方下降的稍微快些,不至于徘徊不前。
缺点:由于是累积梯度的平方,到后面 G t G_t Gt累积的比较大,会导致梯度 α G t + ε → 0 \frac{\alpha }{\sqrt{G_t }+\varepsilon } \rightarrow0 Gt+εα→0 导致梯度消失。
关于AdaGrad,goodfellow和bengio的《deep learning》书中对此的描述是:在凸优化中,AdaGrad算法具有一些令人满意的理论性质。但是,在实际使用中已经发现,对于训练深度神经网络模型而言,从训练开始时累积梯度平方会导致学习率过早过量的减少。AdaGrad算法在某些深度学习模型上效果不错,但不是全部。
具体到实现,对于 iteration t,compute on current mini−batch:

其中 ε \varepsilon ε 一般默认取 1 0 − 7 10^{-7} 10−7(《deep learning》书和mxnet),学习率 α \alpha α 一般取值为 0.01(论文:《An overview of gradient descent optimization algorithms》)。
代码实现:
6. Adadelta
Adadelta是对Adagrad的改进,主要是为了克服Adagrad的两个缺点(摘自Adadelta论文《AdaDelta: An Adaptive Learning Rate Method》):
- the continual decay of learning rates throughout training the need
- for a manually selected global learning rate
为了解决第一个问题,Adadelta只累积过去 w 窗口大小的梯度,其实就是利用前面讲过的指数加权平均,公式如下:
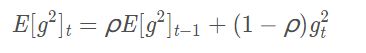
根据前面讲到的指数加权平均,比如当 ρ = 0.9 \rho = 0.9 ρ=0.9 时,则相当于累积前10个梯度。
为了解决第二个问题,Adadelta最终的公式不需要学习率 α \alpha α。Adadelta的具体算法如下所示(来自论文《AdaDelta: An Adaptive Learning Rate Method》)

可以看到adadelta算法不在需要学习率,p.s:看了keras和Lasagne框架的adadelta源码,它们依然使用了学习率,不知道为什么。。。而chainer框架则没有使用。
按照我们的习惯重新写下上述公式:

其中 ε \varepsilon ε 是为了防止分母为0,通常取 1 e − 6 1e^-6 1e−6 。
7.RMSprop(root mean square prop)
RMSprop是hinton老爷子在Coursera的《Neural Networks for Machine Learning》lecture6中提出的,这个方法并没有写成论文发表(不由的感叹老爷子的强大。。以前在Coursera上修过这门课,个人感觉不算简单)。同样的,RMSprop也是对Adagrad的扩展,以在非凸的情况下效果更好。和Adadelta一样,RMSprop使用指数加权平均(指数衰减平均)只保留过去给定窗口大小的梯度,使其能够在找到凸碗状结构后快速收敛。直接来看下RMSprop的算法(来自lan goodfellow 《deep learning》):

在实际使用过程中,RMSprop已被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习人员经常采用的优化算法之一。keras文档中关于RMSprop写到:This optimizer is usually a good choice for recurrent neural networks.
按照我们的习惯,重写下公式:

同样 ε \varepsilon ε 是为了防止分母为0,默认值设为 1 e − 6 1e^{-6} 1e−6。 β \beta β 默认值设为 0.9,学习率 α \alpha α 默认值设为 0.001。
8.Adam(Adaptive Moment Estimation)
Adam实际上是把momentum和RMSprop结合起来的一种算法,算法流程是(摘自adam论文)

同样,简洁的写一下公式:

其中,几个参数推荐的默认值分别为: α = 0.001 , β 1 = 0.9 , β 2 = 0.999 , ε = 1 0 − 8 \alpha = 0.001,\beta_1 = 0.9,\beta_2 = 0.999,\varepsilon = 10^{-8} α=0.001,β1=0.9,β2=0.999,ε=10−8
。t 是迭代次数,每个mini-batch后,都要进行 t += 1。
实践表明,Adam算法在很多种不同的神经网络结构中都是非常有效的。
8. 该如何选择优化算法
介绍了这么多算法,那么我们到底该选择哪种算法呢?目前还没有一个共识,schaul et al 在大量学习任务上比较了许多优化算法,结果表明,RMSprop,Adadelta和Adam表现的相当鲁棒,不分伯仲。Kingma et al表明带偏差修正的Adam算法稍微好于RMSprop。总之,Adam算法是一个相当好的选择,通常会得到比较好的效果。
In summary, RMSprop is an extension of Adagrad that deals with its radically diminishing learning rates. It is identical to Adadelta, except that Adadelta uses the RMS of parameter updates in the numerator update rule. Adam, finally, adds bias-correction and momentum to RMSprop. Insofar, RMSprop, Adadelta, and Adam are very similar algorithms that do well in similar circumstances. Kingma et al. [10] show that its bias-correction helps Adam slightly outperform RMSprop towards the end of optimization as gradients become sparser. Insofar, Adam might be the best overall choice
参考文献:
[1]https://blog.csdn.net/u012328159/article/details/80311892