清橙A1363. 水位 - 清华大学2012年信息学优秀高中学子夏令营

问题描述
　　有一个正方形的地区，该地区特点鲜明：如果把它等分为N×N个小正方形格子的话，在每个格子内的任意地点的地表高度是相同的，并且是一个0到M之间的整数。正方形地区的外部被无限高的边界包围。
　　该地区可能会有积水。经过多年的观察，人们发现了几个关于积水的重要规律：
　　1. 每个格子要么完全没有积水，要么它内部的任意地点的水面高度都是相同的。并且水面高度一定大于地表高度。
　　2. 每个格子的水面高度在0~M之间，并且一定是整数。
　　3. 对于相邻（必须为边相邻）的两个格子，一定不会出现水自动从一个格子流向另一个格子的情况。也就是说，一定不能出现这两个格子都有水且水面高度不同，或者有水格子的水面比无水格子的地表要高的情况。
　　例如，下面图中每个格子里有两个数a/b，说明该格子的地表高度是a，水面高度是b（均为海拔高度），而没有水的格子中b以“−”表示。则左边的情况是符合规律的，而右边的情况并不符合以上规律，因为水可以由2/4的格子流向3/−的格子。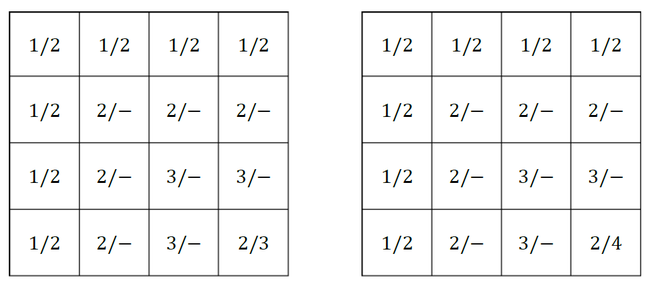

　　(图1)


　　该地区水文站的工作人员小A想知道，该地区中有多少种不同的水位情况符合规律。你能回答他的这个问题吗？
输入格式
　　输入文件的第一行包含两个正整数N和M。
　　随后的N行，每行包含N个非负整数。其中第i+1行的第j个数表示该地区第i行第j列格子的地表高度。
输出格式
　　输出文件只包含一个整数，即该地区符合规律的水位情况种数。
样例输入
4 3
1 1 1 1
1 2 2 2
1 2 3 3
1 2 3 2
样例输出
6
对样例的说明
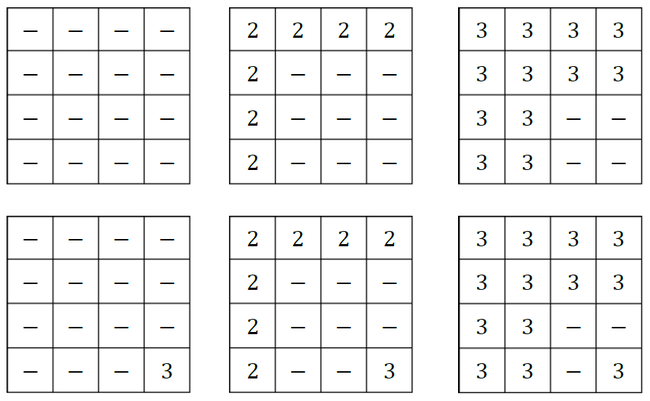
　　符合规律的水位情况有以下六种 ：

数据规模和约定

 

 

好一个并查集

首先我们正着想，一开始都有模模糊糊的这个想法，就是划分区域，这几个区域的水一旦高于分界线的高度就会汇合，所以先计算出水位低于分界线的方案数，再算高于分界线的方案数

显然，低于这个高度的方案数是这几个区域的方案数的乘积，高于这个高度的方案数就是最高限制-这个高度，这几个区域的方案数可以递归做

但是递归又难写，时间上也不允许

所以我们从小到大枚举分界线的高度，把这个格子四周的区域合并，一直到整个区域，用并查集维护区域的信息

WA了好多次，原因是高精度数空间没开够，囧......

  1 const
  2     maxn=103;
  3     s=10000000;
  4     fx:array[1..4]of longint=(1,0,-1,0);
  5     fy:array[1..4]of longint=(0,1,0,-1);
  6 type
  7     point=record
  8       x,y:longint;
  9     end;
 10     big=array[0..2000]of int64;
 11 var
 12     a:array[0..maxn,0..maxn]of longint;
 13     b:array[0..maxn*maxn]of point;
 14     f,h:array[0..maxn*maxn]of longint;
 15     ans:array[0..maxn*maxn]of big;
 16     n,m:longint;
 17 
 18 operator *(var a,b:big)c:big;
 19 var
 20     i,j:longint;
 21 begin
 22     fillchar(c,sizeof(c),0);
 23     for i:=1 to a[0] do
 24       for j:=1 to b[0] do
 25         inc(c[i+j-1],a[i]*b[j]);
 26     c[0]:=a[0]+b[0]-1;
 27     for i:=1 to c[0]-1 do
 28       begin
 29         inc(c[i+1],c[i]div s);
 30         c[i]:=c[i]mod s;
 31       end;
 32     while c[c[0]]>=s do
 33       begin
 34         c[c[0]+1]:=c[c[0]]div s;
 35         c[c[0]]:=c[c[0]]mod s;
 36         inc(c[0]);
 37       end;
 38 end;
 39 
 40 procedure add(var a:big;b:longint);
 41 var
 42     i:longint;
 43 begin
 44     inc(a[1],b);
 45     i:=1;
 46     while a[i]>=s do
 47       begin
 48         inc(a[i+1],a[i]div s);
 49         a[i]:=a[i]mod s;
 50         inc(i);
 51       end;
 52     if i>a[0] then a[0]:=i;
 53 end;
 54 
 55 function calc(i,j:longint):longint;
 56 begin
 57     exit((i-1)*n+j);
 58 end;
 59 
 60 function find(x:longint):longint;
 61 begin
 62     if f[x]=x then exit(x);
 63     f[x]:=find(f[x]);
 64     exit(f[x]);
 65 end;
 66 
 67 procedure swap(var x,y:point);
 68 var
 69     t:point;
 70 begin
 71     t:=x;x:=y;y:=t;
 72 end;
 73 
 74 procedure sort(l,r:longint);
 75 var
 76     i,j,y:longint;
 77 begin
 78     i:=l;
 79     j:=r;
 80     y:=a[b[(l+r)>>1].x,b[(l+r)>>1].y];
 81     repeat
 82       while a[b[i].x,b[i].y]<y do
 83         inc(i);
 84       while a[b[j].x,b[j].y]>y do
 85         dec(j);
 86       if i<=j then
 87       begin
 88         swap(b[i],b[j]);
 89         inc(i);
 90         dec(j);
 91       end;
 92     until i>j;
 93     if i<r then sort(i,r);
 94     if j>l then sort(l,j);
 95 end;
 96 
 97 procedure print(a:big);
 98 var
 99     i:longint;
100     k:int64;
101 begin
102     write(a[a[0]]);
103     for i:=a[0]-1 downto 1 do
104       begin
105         k:=s div 10;
106         while k>1 do
107           begin
108             if a[i]<k then write(0)
109             else break;
110             k:=k div 10;
111           end;
112         write(a[i]);
113       end;
114 end;
115 
116 procedure main;
117 var
118     i,j,x,y:longint;
119 begin
120     read(n,m);
121     for i:=1 to n do
122       for j:=1 to n do
123         begin
124           read(a[i,j]);
125           h[calc(i,j)]:=a[i,j];
126           b[calc(i,j)].x:=i;
127           b[calc(i,j)].y:=j;
128         end;
129     sort(1,n*n);
130     for i:=1 to n*n do
131       begin
132         f[i]:=i;
133         ans[i][0]:=1;
134         ans[i][1]:=1;
135       end;
136     for i:=1 to n*n do
137       for j:=1 to 4 do
138         if (b[i].x+fx[j]>0) and (b[i].x+fx[j]<=n) and (b[i].y+fy[j]>0) and (b[i].y+fy[j]<=n) then
139         begin
140           x:=find(calc(b[i].x,b[i].y));
141           y:=find(calc(b[i].x+fx[j],b[i].y+fy[j]));
142           if (h[x]>=h[y]) and (x<>y) then
143           begin
144             add(ans[y],h[x]-h[y]);
145             ans[x]:=ans[x]*ans[y];
146             f[y]:=x;
147           end;
148         end;
149     add(ans[find(1)],m-a[b[n*n].x,b[n*n].y]);
150     print(ans[find(1)]);
151 end;
152 
153 begin
154     main;
155 end.

View Code