[论文阅读](不确定性系列)
文章目录
- 一. Uncertainty-guided graph attention network for parapneumonic effusion diagnosis
- 摘要
- 引言
- 相关工作
- 提出方法
-
- Graph construction
-
- Bayesian convolutional neural networks
- Graph representation
- Uncertainty-guided graph attention network (UG-GAT)
- 实验结果
-
- Data description
- Baseline and implementation details
- 二. Uncertainty-aware Self-ensembling Model for Semi-supervised 3D Left Atrium Segmentation
- 摘要
- 引言
- 方法
-
- Semi-supervised Segmentation
- Uncertainty-Aware Mean Teacher Framework
- Technique Details
- 三.Depth Uncertainty in Neural Networks
- 摘要
- 引言
- Related Work
- Depth Uncertainty Networks
-
- Probabilistic Model概率模型: Depth as a Random Variable
- Inference in DUNs
一. Uncertainty-guided graph attention network for parapneumonic effusion diagnosis
摘要
-
肺积液(PPE)是一种常见的情况,导致死亡的肺炎住院患者。在计算机断层扫描(CT)中快速区分复杂和非复杂PPE,即CPPE和UPPE具有重要意义。然而,UPPE和CPPE在CT扫描中表现出相似的外观,无论是人类专家还是任何现有的疾病分类方法,都很难通过单一的2D CT图像将CPPE与UPPE区分开来。三维卷积神经网络(cnn)可以利用整个三维体积进行分类:然而,它们通常存在过拟合的固有缺陷。因此,开发一种既能克服3D cnn对内存和计算量的高要求,又能充分利用3D信息的方法是非常重要的。
-
在本文中,我们提出了一种不确定导向的图注意网络(UG-GAT),它可以自动从一个3D卷中提取和集成所有CT切片的信息,并将其分类为UPPE、CPPE和正常对照病例。具体地说,我们把不同情况的区别框定为一个图分类问题。每个个体被表示为一个具有拓扑结构的有向图,其中顶点表示切片的图像特征,边表示它们之间的空间关系。为了估计每个切片的贡献,我们首先使用贝叶斯CNN提取带有不确定性的切片表示:然后我们利用不确定性信息在图预测阶段对每个切片进行加权,以使决策更可靠。本研究构建了302例不同受试者(99例UPPE、99例CPPE和104例正常对照)的胸部CT容积数据集,据我们所知,这是首次尝试使用深度学习方法对UPPE、CPPE和正常对照进行分类。大量实验表明,我们的方法在需求方面是轻量级的,并且在很大程度上优于公认的最新方法。
引言
-
肺旁腔积液(PPE)是一种与肺部感染相关的胸腔积液,在20% - 40%的住院患者中存在。根据液体特征和发病机制,ppe分为不复杂或复杂(即UPPE或CPPE) (Sahn, 2007年)。与UPPE相比,如果胸腔间隙没有充分引流,则CPPE的发生显著增加了发病率和死亡率(Colice et al., 2000)。一般情况下,UPPE只需抗生素治疗即可治愈,而CPPE患者需要胸腔引流(Light, 2006)。因此,UPPE和CPPE的鉴别对临床医生来说,早期治疗至关重要,以便制定个性化的治疗方案。
-
近年来,深度学习方法在各种医学图像分析任务中显示出越来越多的成功。虽然目前还没有在PPE检测中应用,但深度卷积神经网络(cnn)已被用于开发其他肺部相关疾病的先进CAD方法,例如肺癌检测,肺结节的分类和肺炎筛查。现有工作大多采用CT二维切片作为cnn的输入,这些二维切片缺乏深度信息,无法捕捉到肺部病变的真实空间分布。
_第2张图片](http://img.e-com-net.com/image/info8/20e3f642b2694c5d8c7553871ec6e144.jpg)
-
CPPE与UPPE的成像外观有相当大的相似性(如图1所示),在任何单个病例中,仅通过2D CT切片无法将CPPE与UPPE区分开来。例如,CPPE与UPPE有一些共同的图像特征,如存在双侧胸腔积液,呈液体样均匀密度。在临床实践中,胸腔积液分析或细菌培养通常需要胸腔穿刺术(Light, 2006)。CPPE与UPPE在影像学表现上的主要区别是,CPPE患者可能有胸膜微泡、脏器胸膜增厚、壁层胸膜增厚(Ferreiro etal ., 2015)。**然而,由于缺乏空间信息,这些症状很难在二维图像中识别或表征。**精确描述病变的空间形态对于通过CT成像区分两种感染类型至关重要,3D CNN可能通过利用整个3D体积来实现这一点。然而,由于参数数量众多,要想获得一个训练有素、功能强大的3D CNN模型,需要一个大规模的带注释的训练数据集,这对于PPE分类任务来说是一个挑战,因为涉及伦理问题和昂贵的成像成本。
-
因此,开发一种不依赖大规模训练数据集,但仍然可以有效模拟病变分布的方法是非常可取的。图结构方法可以模拟不同CT切片之间的结构连续性和相互作用(Zhou等人,2021年),而图神经网络(GNN)与3D CNN相比参数效率更高。大多数现有的基于图神经网络(GNN)的方法利用所有对象来构建图,其中图上的给定节点代表单个对象的成像数据,边缘建立每对对象之间的交互(Wang等人,2021;Liang等,2021)。这意味着图的拓扑结构受到对象数量和特征的限制。如果一个新的对象需要诊断,那么GNN必须重新训练。
-
不确定性度量可以提供关于图像可靠性和内容的信息,使模型能够主动选择高置信度的数据,减少对训练样本的依赖。 为此,在本文中,我们提出了一个新的不确定性导向的基于图的框架,用于UPPE、CPPE和普通控制类的分类。我们使用不确定性来表示来自CT扫描每个薄片的图像特征的可靠性:这使GNN能够自适应融合CT扫描的不同确定性的图像特征,以帮助决策,从而促进分类过程。
-
与二维和三维cnn相比,我们的方法不仅绕过了对大规模标注数据集的要求,而且避免了三维cnn由于高维体输入而导致的过拟合缺陷,而且利用了不同切片之间的空间关系。 这是通过图和不确定性建模的结合来实现的:每个CT体积与固定拓扑结构表示为一个有向图,在节点组成的图像片和不确定性的特点,和边编码片之间的关系,以确保信息周围的节点更新图时考虑节点和分类图。为每个节点引入不确定性建模,使模型能够在有限的训练数据下,通过主动关注不确定性较小的关键部分和症状,做出可靠的决策。具体来说,我们利用贝叶斯CNN获得切片表示和对应的不确定性,然后用这些不确定性来构造图,在图分类过程中对节点特征重新加权进行信息融合。
-
我们的工作主要贡献如下:
-
据我们所知,这是首次使用深度学习方法对UPPE、CPPE和正常病例进行区分和分类。
-
我们提出了一种不确定性导向的图注意网络(UG-GAT)来捕捉和表示给定三维体数据的空间信息和丰富的上下文信息,以提高分类性能。
-
为了减少数据噪声和不确定性,我们提出不确定性度量作为模型的指导,并进一步集中于最显著的部分和症状,这有助于网络绕过对大规模注释数据集的需求。
相关工作
基于神经网络和不确定性的疾病诊断:
- Veli ckovi c等人(2018)提出了图注意网络(GAT)方法,其中加入了一种注意机制,以便有选择地关注每个顶点的相邻顶点。最近,由于GNN在处理复杂图形数据方面的优势,已被用于自动疾病诊断。Parisot等人(2018)利用图卷积网络(GCN)综合成像和非成像特征来预测阿尔茨海默病(AD)的转换。Wang等人(2021年)首先应用多个不同配置的cnn来提取特征:然后利用GCN融合这些特征,并为最终的Covid-19分类创建一个关系感知表示。Liang等人(2021)在GCN中提出了一个COVID-19图,以合并多个数据集,将COVID-19感染病例与正常对照区分开来。这些基于gnn的方法使用所有主题来构建图,图上的特定节点代表主题的成像数据,边缘建立每对对象之间的交互。这表明该图的拓扑受对象数量的限制:如果需要诊断新的对象,则需要对GNN进行重新训练。
- 不确定性度量可以为人类或自主模型提供有价值的信息,以评估哪些受试者需要进一步的详细检查,并有助于减少误分类的风险。Leibig等人(2017)应用Bayesian CNN获得的不确定性来引用一个困难案例子集,提高了眼底图像对糖尿病视网膜病变(DR)的检测性能。Ghoshal和Tucker(2020)也通过根据不确定性选择训练图像,实现了x射线图像中COVID- 19分类的性能提升。Cicalese等人(2020)利用不确定性对噪声数据进行过滤,提高了肾脏凯夫勒库普斯肾炎分级的性能。在医学图像分类中,不确定性主要用于训练样本的选择,以降低训练噪声,从而提高分类精度。
提出方法
在本节中,我们将展示所提方法的细节。它包括图的构建阶段和不确定性引导的图注意网络。该方法的总体结构如图2所示。
_第3张图片](http://img.e-com-net.com/image/info8/002ea201209b488f897926b6e5fd66a2.jpg)
Graph construction
图的精确区分能力依赖于图像特征的准确表示和相互依赖表征(Parisot et al., 2018), cnn可用于从原始CT图像中提取表征。对不确定性的考虑和衡量对于决策至关重要:知道我们可以信任的图像表示的置信度将有助于,并解释随后的图分类。因此,我们首先应用贝叶斯CNN来获取每一幅CT图像的图像特征及其对应的不确定性,然后用这些数据来构建每个受试者的图。
Bayesian convolutional neural networks
-
cnn很难提供可靠的预测结果,尽管他们有能力提取一般数据驱动的高表达特征(have the ability to extract general data-driven
highly expressive features)(Shridhar等人,2019年)。贝叶斯神经网络(BNN)可以通过模型参数的概率解释来克服这一问题。除了预测不确定性估计,bnn 对过拟合具有鲁棒性 ,可以在小数据集上有效训练(Wang和ye2016;王等,2018)。然而,应用贝叶斯推理的神经网络的计算成本可能很高。虽然可以近似,但我们利用Gal和Ghahramani(2015)中提出的cnn的贝叶斯等效来获得图像表示及其对应的不确定性,这是基于蒙特卡洛Dropout (MC Dropout)方法。MC Dropout是一种用于测量不确定度的强大方法,已被广泛应用于许多应用中(Roy等人,2019;哈珀和南部,2020年)。 -
由于训练数据{x, y},其中x是一组CT图像标签y{0, 1, 2}和{0, 1, 2}分别代表的UPPE,CPPE,和正常的,dropout网络θ(w)可以被训练,其中w是一个取决于dropout的随机变量的有限集。{x*, y*}是一个具有相应预测的新样本。获取给定图像的模型不确定性非常简单,只需在测试时保持退出机制打开并执行多个预测即可。预测分布的宽度是模型不确定性的合理代表。具体地说,我们用蒙特卡罗抽样方法逼近积分,计算预测均值为
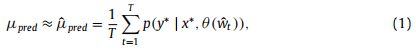
式中,T为蒙特卡罗抽样的总数,wt为第T次抽样的不同dropped unit状态。θ(·)和p(·)分别表示贝叶斯CNN的参数和概率输出。预测标准差作为与预测相关的不确定性的代理被定义为

我们遵循Leibig et al.(2017),设置T = 100来提高不确定性估计的质量
Graph representation
- 我们使用ResNet (He et al., 2016)作为Bayesian CNN骨干,并使用CT图像及其对应标签训练分类模型,在切片水平上诊断UPPE、CPPE和正常对照组。然后我们使用训练有素的贝叶斯CNN进行提取所有图像特征及其不确定性用于图的构造。如图2所示,我们使用GAP层后的特征向量作为每个切片的表示,图中的每个节点特征
![]()
是一个512维的1维特征向量
_第4张图片](http://img.e-com-net.com/image/info8/d21833354e6344038f5cda55c0f152ef.jpg)
不同的图构造策略:(A)无向图(B)有向图。我们使用有向图而不是无向图,以保证中心节点在更新顶点特征时能考虑到所有其他节点,而其他节点只能考虑相邻节点,不受其他无关节点的影响。蓝色和绿色的节点分别代表切片特征和中心节点特征。由于CT体积大小为224 224 64像素(详见4.1节),在我们的实现中,完整的图由64个切片节点和1个中心节点组成。
-
图结构提供了更广泛的视图字段,它根据邻居过滤节点特性的值,而不是孤立地处理每个特性。为了准确地对节点特征之间的交互进行建模,需要对图的拓扑结构进行细致的设计。我们的方法的图拓扑如图3 (B)所示。受试者的每一次CT扫描都表示为一个有向图:顶点由切片特征组成,边缘编码这些切片特征之间的空间关系。我们将图描述为G = (V, A),其中V包含N+1个顶点,
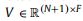
,其中N为每个主题的CT切片数,F为每个节点特征的维数。
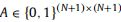
是一个稀疏邻接矩阵,表示顶点之间的边连接,其中Ai,j = 1表示顶点Vi有边连接到顶点Vj,而Ai,j = 0表示顶点Vj没有边连接。CT体中两个相邻切片的图节点通过有向边相互连接,每个图像节点通过边与中心节点连接。图3 (B)中的蓝色和绿色节点分别代表切片特征和中心节点特征。在我们的实现中,由于CT体积大小为224* 224 *64像素(详见4.1节),整个图由64个切片节点和1个中心节点组成。因此,一个图总共有65个顶点和127条边(即63条双向边和64条单向边)。 -
中心顶点为CT体序列信息在图内的有效编码提供了一个集中有效的机制,并在图分类过程中帮助图神经网络处理和集成来自不同切片的信息。经过经验检验,中心顶点的特征使用全0向量初始化。与无向图相比,我们提出的有向图可以保证更新顶点特征时中心节点可以考虑到所有其他节点,而其他节点只考虑自己的邻近节点,不受无关节点的影响。
Uncertainty-guided graph attention network (UG-GAT)
-
图构建完成后,将每个被试的CT数据表示为图G, Bayesian CNN得到的图节点的不确定性存储在向量U中,向量U的大小为(N + 1), (N + 1)为图节点个数。由于中心节点是用来处理和整合信息的,所以我们将其不确定性设为0。为了利用不确定性信息进行决策,我们提出了一种不确定性导向的图注意网络(UG-GAT)。这与图注意层不同(Veli ckovi c等人,2018),因为除了执行自我注意,我们还在更新节点特征时对每个顶点进行不确定性加权。
-
这里我们解释一个不确定性引导的图注意层。取一个构造好的图G = (V, A),它有一组节点特征,
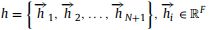
作为输入,UG-GAT层产生一个新的节点特性,即:
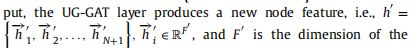
F’是每个节点的新特征的维度。他的学习过程详细如下。 -
第一步,每个节点被施加一个用权重矩阵W参数化的共享线性变换。然后,利用自我注意机制计算节点js特征相对于节点i的重要性的注意系数eij
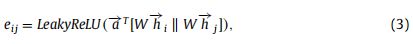
其中||是拼接操作,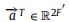 是由LeakyReLU非线性的全连接层实现的参数化权向量(负输入斜率α = 0.2)。
是由LeakyReLU非线性的全连接层实现的参数化权向量(负输入斜率α = 0.2)。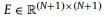
为注意系数矩阵。然后利用不确定性矩阵对注意系数进行重新加权,确保不确定性较大的节点特征对其他节点的影响较小,同时允许不确定性较小的节点在决策过程中发挥更大的作用。为此,我们首先对之前得到的不确定性向量U进行归一化,将其元素值设置在0到1之间:

其中σ是一个小的正数,为稳定设置为1 *10e-8,以避免分母为零的情况。Min(·)和max(·)分别表示向量的最大值和最小值。调整权重的操作定义为:

其中Diag()就是对角化操作。然后,利用softmax函数对系数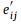 进行归一化处理为了使它在不同节点之间具有可比性:
进行归一化处理为了使它在不同节点之间具有可比性:
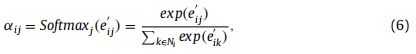
式中,Ni为图中节点i的邻域,即只考虑邻域节点j∈Ni的eij,以避免涉及任何无关节点。最后使用归一化的注意系数αij来计算相关特征的加权和,作为每个节点的最终输出特征:

其中ELU表示指数线性单元(ELU)非线性。我们使用多头注意来稳定自我注意的学习过程。 -
为了避免由于过平滑问题导致的性能下降(Chen et al., 2020),我们的UG-GAT由三个隐藏层组成,其中第一层是不确定性导向的图注意层,其他是图注意层。我们没有在最后一层对所有节点特征进行平均,而是将中心节点的特征作为最终的集成特征:它通过softmax激活层进行目标分类。
实验结果
Data description
- 为了保证不同方法之间的公平比较,我们在训练阶段使用相同的数据增强方法(即颜色抖动和随机旋转),所有的实验都保持输入大小为224 224 64像素。
- 每个受试者的CT卷标为0、1或2,分别代表UPPE、CPPE和正常对照组。我们对所有302例病例进行了5次交叉验证,以便在这个相对较小的数据集上进行更可靠的分析。我们将这些病例分成5个子集,每个子集的被试人数相近。对于每个折叠,我们使用4个子集进行训练,其余子集用于测试。
- 此外,为了训练Bayesian CNN,获得每个受试者的切片表示及其对应的不确定度,由专业放射科医师标记了2441张在UPPE和CPPE体积中有病变的切片(即1254张UPPE和1187张CPPE)。我们还选择了1590个正常的控制片。最后,用4031个切片训练贝叶斯CNN。值得注意的是,这些切片不是来自用于评估UG-GAT的302个候选样本,这确保了在计算不确定性时,在模型训练阶段没有看到数据。
Baseline and implementation details
- 我们分别训练Bayesian CNN和UG-GAT。具体来说,我们首先训练贝叶斯CNN,然后用它来产生切片特征和相应的不确定性。然后,利用构造的图对UG-GAT进行训练
- 为了评价提出的方法,我们将UG-GAT与之前提出的几种利用3D数据进行医学图像分类的方法进行了比较。这些方法中的大多数(Khawaldeh等人,2018;Chang等人,2018;周等,2019;Liu等,2020;Zunair et al., 2020)以三维体数据为输入,应用不同架构的三维cnn提取特征进行分类。(Hao et al., 2021)首先利用CNN提取特征,然后利用ConvLSTM融合信息,得到不同类别的概率。
二. Uncertainty-aware Self-ensembling Model for Semi-supervised 3D Left Atrium Segmentation
摘要
-
深度卷积神经网络的训练通常需要大量的标记数据。然而,在医学图像分割任务中,对数据进行标注是昂贵和耗时的。在本文中,我们提出了一种新的不确定性感知的半监督框架(uncertainty-aware semi-supervised framework),用于从三维磁共振图像中分割左心房。
-
我们的框架可以有效地利用未标记数据,鼓励在不同扰动下对相同的输入进行一致的预测。具体来说,该框架由学生模型和教师模型组成,学生模型通过最小化教师模型目标的分割损失和一致性损失来学习教师模型。我们设计了一种新颖的不确定性感知方案,使学生模型能够利用不确定性信息逐步从有意义和可靠的目标中学习。实验结果表明,该方法通过加入未标记数据获得了较高的性能增益。我们的方法优于最先进的半监督方法,展示了我们的框架在具有挑战性的半监督问题中的潜力。
引言
- 磁共振(MR)图像中左心房(LA)的自动分割对促进房颤的治疗具有重要意义。深度学习有了大量的标注数据,极大地推进了LA[15]的分割。然而,在医学成像领域,由经验丰富的专家以一种切片的方式从3D医学图像中勾画出可靠的注释是昂贵和乏味的。由于无标记数据通常是丰富的,我们重点研究了利用有限的标记数据和丰富的无标记数据进行LA分割的半监督方法。
- 大量的工作致力于利用未标记数据来提高医学图像社区的分割性能[1,2,3,7,19]。例如,Bai等人[1]介绍了一种基于自我训练的心脏MR方法图像分割,其中网络参数和未标记数据分割交替更新。此外,对抗学习也被用于半监督学习[6,12,18]。Zhang等人[18]设计了一个深度对抗网络,通过鼓励将未标注的图像分割成与标注的图像相似的样子来使用未标注的图像。另一种方法[12]利用对抗网络选择未标记数据的可信区域来训练分割网络。由于自集成方法在半监督自然图像分类方面取得了良好的结果[9,14],Li等人[10]将Π-model[9]扩展为变换一致的半监督皮肤病变分割方法。其他方法[5,13]利用加权平均一致性目标进行半监督MR分割。虽然取得了很好的进展,但这些方法没有考虑目标的可靠性,这可能导致无意义的指导。
- 在本文中,我们提出了一种新的不确定性感知的半监督学习框架,通过额外利用未标记数据从3D MR图像中分割左心房。我们的方法鼓励分割预测在相同输入的不同扰动下是一致的,遵循相同的精神mean teacher[14]。具体来说,我们构建了教师模型和学生模型,其中学生模型通过最小化教师模型对标记数据的分割损失和最小化教师模型对所有输入数据的目标一致性损失来学习教师模型。**如果在未标记的输入中没有提供ground truth,教师模型的预测目标可能是不可靠的和嘈杂的。**为此,我们设计了不确定性感知的平均教师(UA-MT)框架,在该框架中,学生模型通过利用教师模型的不确定性信息,逐步从有意义和可靠的目标中学习。具体来说,教师模型除了生成目标输出外,还利用蒙特卡罗抽样估计每个目标预测的不确定性。 在估计不确定性的指导下,我们在计算一致性损失时过滤掉不可靠的预测,只保留可靠的(低不确定性)。因此,学生模型得到了优化,**有了更可靠的监督,反过来也鼓励教师模式产生更高质量的目标。**我们的方法在MICCAI 2018心房分割挑战的数据集上进行了广泛的评估。结果表明,我们的半监督方法通过利用未标记数据,在LA分割方面取得了很大的改进,并且也优于其他先进的半监督分割方法。
方法
_第7张图片](http://img.e-com-net.com/image/info8/04f6283592a846af82dfff1ff43fee57.jpg)
半监督分割的不确定性感知框架的流水线。通过最小化有标记数据DL上的监督损失Ls和无标记数据DU和有标记数据DL上的一致性损失Lc来优化学生模型。来自教师模型的估计不确定性引导学生从教师那里学习更可靠的目标。
图1展示了我们用于半监督LA分割的不确定性感知自集成平均教师框架(UA-MT)。教师模型为学生模型生成学习目标,并对目标的不确定性进行估计。不确定性导向的一致性损失改善了学生模型,提高了框架的鲁棒性。
Semi-supervised Segmentation
- 我们研究了三维数据的半监督分割任务,其中训练集由N个标记数据和M个未标记数据组成。我们表示标记集DL = {(xi, yi)}N_i=1,未标记集DU = {xi}N+M_i=N +1,其中xi R_H W D是输入体积,yi {0,1}H W D是ground-truth注解。我们的半监督分割框架的目标是最小化以下组合目标函数:
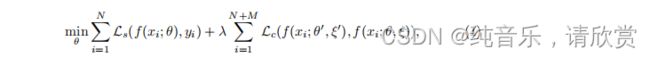
**Ls表示监督损失(例如,交叉熵损失)**来评估网络输出的质量标签输入,和Lc代表无监督一致性损失来衡量教师网络和学生模型在相同的输入ξ不同扰动下的预测一致性。其中,f(·)为分割神经网络;(θ’, ξ’)和(θ, ξ)分别表示教师模型和学生模型的权值和不同的扰动操作(如输入加噪声和网络割除)。λ是一个梯度加权系数,控制监督和非监督损失之间的权衡。 - 最近的研究[9,14]表明,在不同的训练过程中对网络进行集成预测可以提高预测的质量,将其作为教师预测可以提高结果。因此,我们将教师的权重θ’更新为学生的权重θ的指数移动平均值(EMA),以集成不同训练步骤中的信息。图1所示。具体地说,我们在训练步骤t时将教师权重θ’t更新为:
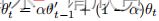
,其中α是控制更新速率的EMA衰减。
Uncertainty-Aware Mean Teacher Framework
- 如果没有标注的输入,教师模型的预测目标可能是不可靠的和有噪声的。因此,我们设计了一个不确定性感知方案,**使学生模型逐渐从更可靠的目标学习。**给定一批训练图像,教师模型不仅生成目标预测,而且估计每个目标的不确定性。然后在不确定性估计的指导下,利用一致性损失优化学生模型,只关注自信目标.
- 估计不确定性。受贝叶斯网络的不确定性估计的启发,我们用蒙特卡罗Dropout[8]估计了贝叶斯网络的不确定性。对每个输入体积,在随机dropout和输入高斯噪声的情况下,对教师模型进行T随机正向传递。因此,对于输入中的每个体素,我们得到一组softmax概率向量:{pt}T_t=1。我们选择预测熵作为近似不确定性的度量,因为它有一个固定的范围[8]。形式上,预测熵可以概括为:
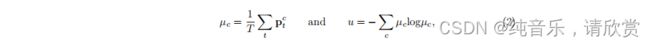
式中PC_T为第t次预测中第c类的概率。注意,不确定度以体素水平估计,整个体积U的不确定度为{U} RH W D。 - Uncertainty-Aware一致性的损失。在估计的不确定性U的指导下,我们过滤掉相对不可靠(高不确定性)的预测,只选择确定的预测作为学生模型的学习目标。特别地,对于我们的半监督分割任务,我们设计了不确定性感知的一致性损失Lc作为教师和学生模型的体素水平均方误差(MSE)损失,仅用于最确定的预测
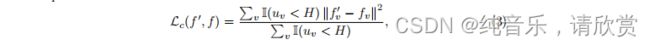
式中,I(·)为指标函数;f’v和fv分别为教师模型和学生模型在第v体素上的预测;u_v为第v体素处估计的不确定度U;**H是选择最确定目标的阈值。**在训练过程中,由于不确定性感知的一致性损失,学生和教师都可以学习到更可靠的知识,从而降低模型的整体不确定性。
Technique Details
-
我们采用V-Net[11]作为我们的网络骨干。我们去除每个卷积块中的短残差连接,并使用联合交叉熵损失和dice损失[16]。为了使V-Net作为贝叶斯网络来估计不确定性,在V-Net的L-Stage 5层和R-Stage 1层之后,增加了两个dropout层,dropout率为0.5。
-
我们在网络训练和不确定度估计中打开dropout,而在测试阶段关闭dropout,因为我们不需要估计不确定度。我们根据经验将EMA衰减α设为0.99,参考之前的工作[14]。在[9,14]之后,我们使用一个时间相关的高斯预热函数λ(t) = 0.1 *e(-5(1- t/tmax)2)来控制监督损失和非监督一致性损失之间的平衡,其中t表示当前的训练步长,tmax是最大的训练步长。这样的设计可以保证在开始时,目标损失由监督损失项主导,避免网络陷入一个退化解,即没有对未标记数据进行有意义的目标预测[9]。对于不确定性估计,我们设T = 8来平衡不确定性估计质量和训练效率。我们还使用相同的高斯上升范式,将不确定性阈值H在Eq.(3)中从3/4Umax上升到Umax,其中Umax是最大的不确定性值(即我们实验中的ln2)。随着训练的进行,我们的方法会过滤出越来越少的数据,让学生从相对确定的情况逐渐学习到不确定的情况。
三.Depth Uncertainty in Neural Networks
摘要
现有的深度学习不确定性估计方法往往需要多个前向传递,这使得它们不适合计算资源有限的应用。为了解决这个问题,我们在神经网络的深度上执行概率推理。不同深度对应的子网络共享权重,其预测通过边缘化(marginalisation)结合在一起,产生模型的不确定性。通过利用前馈网络的连续结构sequential structure,我们能够评估我们的训练目标,并通过一次前向传递进行预测。我们在真实世界的回归和图像分类任务中验证了我们的方法。我们的方法提供了不确定性校准、数据转移的健壮性,以及与计算成本更高的基线相比具有竞争力的准确性。
引言
-
尽管深度学习被广泛采用,但构建提供鲁棒不确定性估计的模型仍然是一项挑战。这对于现实世界的应用尤其重要,因为我们不能期望观察数据的分布与训练数据的分布相同。深度模型往往是病态的过度自信,即使他们的预测是不正确的。如果人工智能系统能够可靠地识别出预期表现不佳的情况,并请求人工干预,那么它们可以更安全地部署在医疗场景(Filos等人,2019年)或自动驾驶汽车(Fridman等人,2019年)等领域。
-
因此,一个快速增长的分支领域已经出现,寻求建立不确定性感知神经网络。遗憾的是,这些方法由于一系列的缺点,很少能从研究到生产的飞跃。1)实现复杂性:它们在技术上很复杂,对超参数选择很敏感。2)**计算成本:它们的收敛时间可能比常规网络长几个数量级,或者需要训练多个网络。**在测试时,通常需要将多个模型的预测取平均值。3)性能薄弱:它们依赖粗糙的近似来实现可伸缩性,往往导致有限或不可靠的不确定性估计(Foong等人,2019a)。
_第9张图片](http://img.e-com-net.com/image/info8/890147df6d3b46368379b485b6e1ee5d.jpg)
图1:一个DUN是由不断增加的子网络组成的(左,颜色表示具有共享参数的层)。这些对应于日益复杂的函数(中心,颜色表示进行预测的深度)。通过这些函数的不一致,对深度的边缘化产生了模型的不确定性(右,误差条表示1标准开发)。Marginalising over depth yields model uncertainty through disagreement of these functions -
在这项工作中,我们引入了深度不确定性网络(DUNs),这是一种将神经网络(NN)的深度作为执行推理的随机变量的概率模型。与神经网络中用于贝叶斯推理的更典型的weight-space方法相比,ours reflects a lack of knowledge about how deep our network should be。我们将**网络权值(network weights)**视为可学习的超参数。**在duns中,在深度上边缘化( marginalising over depth)等同于在一个逐渐加深的神经网络集合上执行贝叶斯模型平均(BMA)。**如图1所示,DUNs利用单个深度网络的过度参数化来生成数据的不同解释。DUNs的主要优点是:
-
1.实现简单:只需要对普通的深度学习代码进行少量的添加,而不需要改变超参数或训练机制。
-
- 廉价的部署:只需一次向前传递,就可以计算出精确的预测后验。
-
3.校准的不确定性:我们的实验表明,DUNs在预测性能、分布外(OOD)检测和对腐败的鲁棒性方面具有很强的基线。
Related Work
- 传统上,贝叶斯通过将深度网络的权重作为随机变量来解决过度自信问题。通过边缘化,权重空间的不确定性被转化为预测。唉,贝叶斯神经网络(BNNs)中的权重后验是棘手的。哈密顿蒙特卡罗(Neal, 1995)仍然是bnn中推理的黄金标准,但扩展性有限。拉普拉斯近似(MacKay, 1992;Ritter等人,2018),变分推理(VI) (Hinton和van Camp, 1993;格雷夫斯,2011;Blundell等人,2015)和期望传播(Hernández-Lobato和Adams, 2015)都被提出作为替代方案。更近期的方法可扩展到大型模型。Gal and Ghahramani(2016)将dropout重新解读为VI,称之为MC dropout。其他随机正则化技术也可以从这个角度来看待(Kingma等人,2015;加,2016;Teye et al., 2018)。这些可以无缝地应用于普通网络。遗憾的是,上述大多数方法依赖于因式近似,通常为高斯近似,导致病理性过度自信(Foong等人,2019a)。
- 目前尚不清楚如何在网络权重上放置合理的先验(Wenzel等人,2020a)。DUNs通过瞄准深度来避免这个问题。BNN推理也可以直接在函数空间中进行。然而,这需要对随机过程之间的KL散度进行粗略的近似。无穷宽神经网络与高斯过程(GPs)的等价性可以用于对bnn进行精确推理。不幸的是,精确的GP推断在数据集大小上很难伸缩。
- 深度集成Deep ensembles是一种用于神经网络不确定性估计的非贝叶斯方法,它训练多个独立网络并聚合它们的预测(Lakshminarayanan等人,2017)。集成提供了非常强大的结果,但受其计算成本的限制。Huang等人(2017年)、garypov等人(2018年)和Maddox等人(2019年)通过利用单一SGD轨迹中发现的不同重量配置来降低训练集成的成本。然而,这是以降低预测性能为代价的(Ashukha等人,2020年)。**与深度集成相似,DUNs结合了来自一组深度模型的预测。**然而,这种集合源于将深度视为随机变量。不同于集成,BMA假设存在一个单一的正确模型(Minka, 2000)。在DUNs中,不确定性的产生是由于缺乏关于正确模型深度的知识。值得注意的是,deep ensembles 也可以解释为近似BMA (Wilson, 2020)。
- 除DUNs外,上述所有方法都需要多次前向传递来产生不确定性估计。这在低延迟设置或计算资源有限的设置中是有问题的。请注意,某些方法,如MC Dropout,可以通过批处理并行化。这允许一些计算时间/内存使用的权衡。另一种方法是,Postels等人(2019)使用误差传播来通过一次前向传递来近似退出预测后验。虽然有效,但这种方法与MC Dropout有相同的缺点。van amersfort等人(2020)将深度RBF网络与雅可比正则化项相结合,以确定地检测OOD点。Nalisnick等人(2019c)和Meinke和Hein(2020)使用生成模型来检测OOD数据,而不需要进行多重预测评估。不幸的是,深度生成模型对于OOD检测可能不可靠(Nalisnick等人,2019b),更简单的替代方案可能难以规模化
- 关于神经网络结构选择的概率推理有丰富的文献,首先是自动关联检测(MacKay et al., 1994)。从那时起,许多方法被引入(Lawrence, 2001;高希等人,2019年)。也许与我们的研究最接近的是Nalisnick等人(2019a)的研究,他们将dropout解释为一种structured shrinkage prior,可以减少ResNets中残留块的影响。相反,可以为任何前馈神经网络构造一个DUN,并在不同深度边缘化预测。Dikov和Bayer(2019)的类似工作使用VI通过利用离散概率分布的连续松弛来学习神经网络的宽度和深度。对于深度,他们使用伯努利分布来模拟任何层用于预测的概率。与他们的方法相比,DUNs使用类别分布(Categorical distribution)来建模深度,不需要采样来评估训练目标或进行预测,并且可以应用于更广泛的神经网络结构,如cnn。Huang等人(2016)将随机drop layers作为ResNet训练规范化方法。另一方面,DUNs在训练和测试期间对架构进行了精确的边缘化,将深度的不确定性转化为广泛的功能复杂性的不确定性。
- DUNs依赖于两种见解,这两种见解最近已经在文献的其他地方得到了证明。第一个是,**单个过参数化的神经网络能够学习数据集的多种多样的表示。**这也是MIMO后续工作的关键洞察(Havasi等人,2020年)。第二,在我们的案例深度中,将具有不同超参数的神经网络集成,可以提高预测的稳健性。与我们的工作同时, hyper-deep ensembles(Wenzel et al., 2020b)在很大范围内的参数中演示了这种特性。
Depth Uncertainty Networks
- 假设数据集
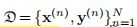
,神经网络由一个输入块 f0(·),D个中间块{fi(·)}D_i=1和一个输出块 fD+1(·)组成。每个块是一组一个或多个堆叠的线性和非线性操作。深度i ->[0, D], a_i的激活递归地得到ai = fi(ai-1), a0 = f0(x)。 - 通过网络的前向传递是一个迭代过程,其中每个连续的块fi(·)细化前一个块的激活。通过将输出块应用到每个中间块的激活,可以在此过程的每一步进行预测:yi = f_D+1(a_i)。图2显示了这个计算模型。可以通过改变一个普通PyTorch NN中的8行来实现,如附录h所示。回顾图1,我们可以利用中间块预测之间的分歧来量化模型的不确定性.
_第10张图片](http://img.e-com-net.com/image/info8/f296c2f2e28b4cd18c78c1915b4ce648.jpg)
图2:左边:考虑中的图形模型。右:计算模型。每一层的激活被传递到输出块,产生每个深度的预测。
Probabilistic Model概率模型: Depth as a Random Variable
- 我们在网络深度上放置了一个 categorical prior分类先验
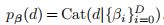
。将网络权值作为θ,我们利用相应子网的输出参数化每个深度的可能性: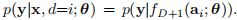
。图2显示了一个图形模型。对于一个给定的权重配置,the likelihood for every depth,因此我们的模型的边际对数可能性 Marginal Log Likelihood(MLL):

可以通过利用前馈神经网络的连续性 sequential nature对训练集进行一次前向传递而获得。The posterior over depth,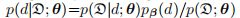
是一种类别分布,它告诉我们每个子网解释数据的能力。
_第11张图片](http://img.e-com-net.com/image/info8/340fbdf4b8bd461dbb19b5faed794dd3.jpg)
图3:最上面一行:训练过程中MLL和ELBO的进展。下:所有六种深度后验概率的进展。左列对应于直接优化MLL,右列对应于VI。对于后者,示出了变分后验概率q(d)。
- 深度神经网络的一个关键优势在于其自动特征提取和表示学习的能力。例如,Zeiler和Fergus(2014)研究表明,cnn在更深的层中依次检测出更抽象的特征。类似地,frost等人(2019)发现,最大化中间层中不同类表示的纠缠可以产生更好的泛化。考虑到这些结果,使用所有的网络中间块进行预测可能是次优的。相反,我们推断每个块是否应该用于学习表征或执行预测,我们可以利用这一点,通过将网络深度作为一个随机变量来进行集成。如图3所示,太浅无法解释数据的子网被赋低后验概率;他们进行特征提取。
Inference in DUNs
-
我们考虑通过直接最大化(1)关于θ,使用反向传播和log-sum-exp技巧来学习网络权值。在附录B中,我们表明,(1)到达每个子网的梯度由相应深度的后团块加权we show that the gradients of (1) reaching each subnetwork are weighted by the corresponding depth’s posterior mass。这将导致局部最优,除一个子网外所有子网的梯度消失。posterior在任意深度塌陷为delta函数,留给我们一个确定性神经网络。在处理大型数据集时,人们可能确实会认为真正的 posterior over depth是一个delta。然而,由于现代的nn甚至对于大型数据集都没有指定,因此多个深度应该能够同时解释数据(如图3和附录B所示)。
-
我们可以通过将网络权值θ的优化与后验分布解耦来避免上述病理。在潜在变量模型中,期望最大化(EM)算法(Bishop, 2007)允许我们通过迭代计算p(d| d;θ),然后更新θ。我们建议使用随机梯度变分推理作为一种更适合神经网络优化的替代方法。我们引入了深度
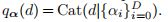
上的替代分类分布。在附录A中,我们推导出(1)的下界如下:

-
该证据下限(ELBO)允许我们利用梯度同时优化变分参数α和网络权θ。因为我们的变分后验和真后验都是绝对的,(2)相对于α是凸的。最优时,
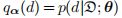
,束缚较紧。因此,我们执行精确推理而不是近似推理。 -
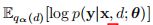 可以由每个深度的激活量来计算。因此,(2)中的两项都可以精确地求值,只需要一次向前传递。这消除了对高方差蒙特卡罗梯度估计的需要,通常在神经网络的VI方法中需要。当使用大小为B的小批次时,我们随机估计(2)中的ELBO为:
可以由每个深度的激活量来计算。因此,(2)中的两项都可以精确地求值,只需要一次向前传递。这消除了对高方差蒙特卡罗梯度估计的需要,通常在神经网络的VI方法中需要。当使用大小为B的小批次时,我们随机估计(2)中的ELBO为:

-
对新数据x的预测是通过使用变分后验边缘化深度(by marginalising depth with the variational posterior )来实现的
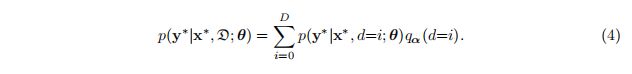
_第1张图片](http://img.e-com-net.com/image/info8/b47bdc9c4005449981d6c9da3ca635fa.jpg)
_第5张图片](http://img.e-com-net.com/image/info8/1480255c672c408ea3bf85df379121e6.jpg)
_第6张图片](http://img.e-com-net.com/image/info8/01ef913e16244dfaa5e5b999806bce18.jpg)
_第8张图片](http://img.e-com-net.com/image/info8/914c2a510ac042af89bd1ce56715ffee.jpg)