【cs229-Lecture17】离散与维数灾难

主要内容：

• 解决MDP问题的算法：

1. 离散化；
2. 模型MDP的同化型； (model/similator)
3. 拟合值迭代算法；
4. Q函数；
5. 近似政策迭代；

---

笔记转自：http://blog.csdn.net/dark_scope/article/details/8252969

连续状态的MDP

之前我们的状态都是离散的，如果状态是连续的，下面将用一个例子来予以说明，这个例子就是inverted pendulum问题

也就是一个铁轨小车上有一个长杆，要用计算机来让它保持平衡(其实就是我们平时玩杆子，放在手上让它一直保持竖直状态)

这个问题需要的状态有：都是real的值

x(在铁轨上的位置)

theta(杆的角度)

x’(铁轨上的速度)

thata'(角速度)

离散化

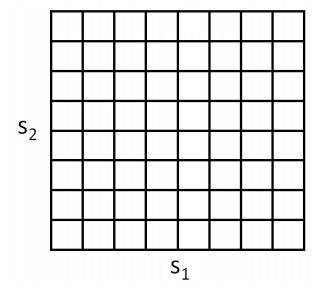
  也就是把连续的值分成多个区间，这是很自然的一个想法，比如一个二维的连续区间可以分成如下的离散值：

但是这样做的效果并不好，因为用一个离散的去表示连续空间毕竟是有限的离散值。

离散值不好的另一个原因是因为curse of dimension(维度诅咒)，因为连续值离散值后会有多个离散值，这样如果维度很大就会造成有非常多状态

从而使需要更多计算，这是随着dimension以指数增长的

simulator方法

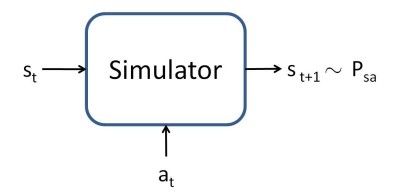
也就是说假设我们有一个simulator，输入一个状态s和一个操作a可以输出下一个状态，并且下一个状态是服从MDP中的概率Psa的分布，即：

这样我们就把状态变成连续的了，但是如何得到这样一个simulator呢？

①：根据客观事实

比如说上面的inverted pendulum问题，action就是作用在小车上的水平力，根据物理上的知识，完全可以解出这个加速度对状态的影响

也就是算出该力对于小车的水平加速度和杆的角加速度，再去一个比较小的时间间隔，就可以得到S(t+1)了

②：学习一个simulator

这个部分，首先你可以自己尝试控制小车，得到一系列的数据，假设力是线性的或者非线性的，将S(t+1)看作关于S(t)和a(t)的一个函数

得到这些数据之后，你可以通过一个supervised learning来得到这个函数，其实就是得到了simulator了。

比如我们假设这是一个线性的函数：

在inverted pendulum问题中，A就是一个4*4的矩阵，B就是一个4维向量，再加上一点噪音，就变成了：其中噪音服从

我们的任务就是要学习到A和B

(这里只是假设线性的，更具体的，如果我们假设是非线性的，比如说加一个feature是速度和角速度的乘积，或者平方，或者其他，上式还可以写作：)

这样就是非线性的了，我们的任务就是得到A和B，用一个supervised learning分别拟合每个参数就可以了

---

连续状态中得Value(Q)函数

这里介绍了一个fitted value(Q) iteration的算法

在之前我们的value iteration算法中，我们有：

这里使用了期望的定义而转化。fitted value(Q) iteration算法的主要思想就是用一个参数去逼近右边的这个式子

也就是说：令

其中是一些基于s的参数，我们需要去得到系数的值，先给出算法步骤再一步步解释吧：

算法步骤其实很简单，最主要的其实就是他的思想：

在对于action的那个循环里，我们尝试得到这个action所对应的，记作q(a)

这里的q(a)都是对应第i个样例的情况

然后i=1……m的那个循环是得到是最优的action对应的Value值，记作y(i)，然后用y(i)拿去做supervised learning，大概就是这样一个思路

至于reward函数就比较简单了，比如说在inverted pendulum问题中，杆子比较直立就是给高reward，这个可以很直观地从状态得到衡量奖励的方法

在有了之上的东西之后，我们就可以去算我们的policy了：

---

确定性的模型

上面讲的连续状态的算法其实是针对一个非确定性的模型，即一个动作可能到达多个状态，有P在影响到达哪个状态

如果在一个确定性模型中，其实是一个简化的问题，得到的样例简化了，计算也简化了

也就是说一个对于一个状态和一个动作，只能到达另一个状态，而不是多个。