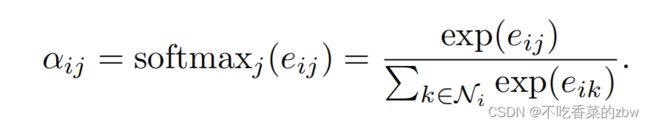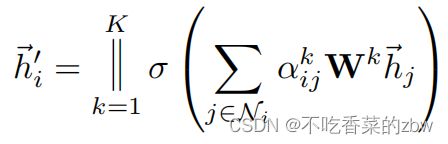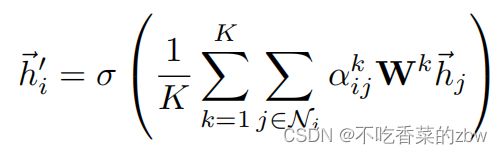论文阅读”Graph attention networks“(ICLR2018)
论文标题
Graph attention networks
论文作者、链接
作者:
Veli{\v{c}}kovi{\'c}, Petar and Cucurull, Guillem and Casanova, Arantxa and Romero, Adriana and Lio, Pietro and Bengio, Yoshua
链接:https://arxiv.org/abs/1710.10903
代码:GitHub - PetarV-/GAT: Graph Attention Networks (https://arxiv.org/abs/1710.10903)
Introduction逻辑(论文动机&现有工作存在的问题)
卷积神经网络(Convolutional Neural Networks ,CNNs)被成功且广泛的应用在网格状的数据结构上。但是其实很多数据并不是网格装的数据,往往是以图的形式展示。
其他的工作中已经有几次尝试扩展神经网络来处理任意结构的图,早期的工作使用递归神经网络来处理以图形式表示的有向无环图数据。图神经网络(Graph Neural Networks,GNNs),作为递归神经网络的一种推广,它可以直接处理更一般的图类,例如循环图、有向图和无向图。GNN使用一种交替处理的方式,将节点状态传播到平衡状态;后接一个神经网络,基于每一个结点的状态,产生一个输出。
不过,众多研究者想在图谱领域生成一个通用的卷积。这方面的进展通常分为光谱spectral方法和非光谱non-spectral方法。
一方面,光谱spectral方法,以图的光谱表示运作,在结点分类已经取得了不错的结果。这些方法,滤波器的学习依赖于拉普拉斯向量偏置,这又依赖于图的结构。所以这个模型在一个具体的图结构上训练,却不能迁移到其他的图结构。
另一方面,非光谱non-spectral的方法,直接在图谱上进行卷积的定义,在空间相邻的邻居上进行操作。这类方法面对的问题是,如何定义在不同尺寸的邻居上的操作,同时保持CNN权重共享的特性。某些情况下,这种模型要求对每一个结点的度学习一个特别的权重矩阵。
注意力机制Attention mechanisms几乎成为一个事实标准(de facto 是一个拉丁语的法学词汇,意思是法律并未承认,但事实上存在的(形容词 & 副词)),在很多基于序列的任务中。注意力机制的一个好处在于,可以处理任何尺寸的输入,专注于输入数据的最有关的部分,以做出决定。当注意力机制被用来计算单个序列的一个表达时,其通常被视为自注意力self-attention或者是内部注意力intra-attention。其他的研究表明,不仅仅是自注意力可以提升基于RNN或者卷积的这类模型的表现,并且也可以构建强力的模型。
受其他研究的启发,作者介绍一个基于注意力的模型架构以执行图结构数据的结点分类。该想法主要是计算图中每一个结点的潜在表达,根据自注意力策略,也顾及到其邻居点。注意力结构有一些有趣的特征:1)这个操作效率很高,可以在结点——邻居对中并行执行;2)它可以通过指定相邻节点的任意权重来应用于具有不同度数的图节点;3)该模型直接适用于归纳学习问题,包括模型必须推广到完全不可见的图的任务。作者还推出了Cora,Citeseer,Pubmed数据集。
论文方法
图注意力层
作者先对单独的图注意力层进行描述,该层用于GAT的架构中的各种位置。
层的输入是一组结点特征,![]() ,其中
,其中![]() 是结点的数目,
是结点的数目,![]() 是特征维度。图注意力层输出一组新的结点特征(基于不同的潜在基底
是特征维度。图注意力层输出一组新的结点特征(基于不同的潜在基底![]() )
)![]() 作为其输出。
作为其输出。
为了的得到足够的表达能力,以将输入的特征转换成高维特征,需要至少一个可学习的线性转换。为此,作为一个初始步骤,对每个节点应用由权重矩阵![]() 参数化的共享线性变换。在结点上应用自注意力机制,
参数化的共享线性变换。在结点上应用自注意力机制,![]() ,以计算注意力系数:
,以计算注意力系数:
该公式代表结点![]() 的特征对结点
的特征对结点![]() 的重要性。在大多数情况下,模型允许每一个结点都去注意其他的每一个结点,丢掉所有的结构信息。通过使用掩膜注意力masked attention,来添加图结构信息;仅仅对
的重要性。在大多数情况下,模型允许每一个结点都去注意其他的每一个结点,丢掉所有的结构信息。通过使用掩膜注意力masked attention,来添加图结构信息;仅仅对![]() 的结点去计算
的结点去计算![]() ,其中
,其中![]() 是结点
是结点![]() 在图中的一些邻居点。在作者的实验中,这些是结点
在图中的一些邻居点。在作者的实验中,这些是结点![]() 的一阶邻居点。为了方便不同结点之间的比较,通过softmax函数对其进行正则化:
的一阶邻居点。为了方便不同结点之间的比较,通过softmax函数对其进行正则化:
在作者的实验中,注意力机制![]() 是一个单层的前馈神经网络,参数为一个参数向量
是一个单层的前馈神经网络,参数为一个参数向量![]() ,使用LeakyReLU作为激活函数。于是上面的公式变为:
,使用LeakyReLU作为激活函数。于是上面的公式变为:
其中,![]()
![]() 表示转置,
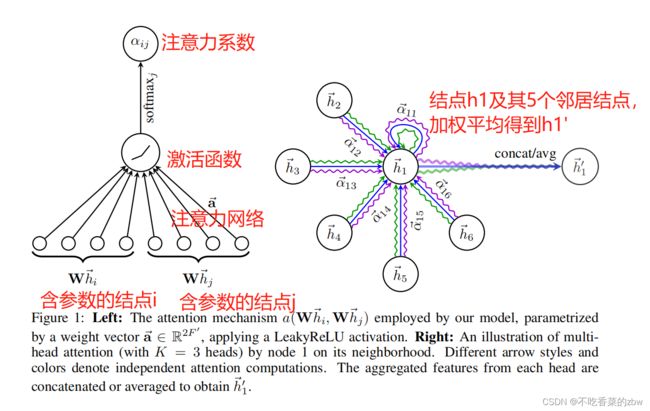
表示转置,![]() 表示连接concatenation。 如图1左边所示:
表示连接concatenation。 如图1左边所示:
一旦得到了正则化的注意力系数,该系数被用来计算其对应特征的线性组合,作为每个节点的最终输出特征:
为了进一步稳定自注意力的训练过程,作者使用多头注意力multi-head attention。具体来说,K个独立注意机制对公式4进行计算,然后将它们的特征进行串联,得到如下输出特征表示:
其中![]() 表示拼接操作,
表示拼接操作,![]() 是正则化的注意力系数,由第
是正则化的注意力系数,由第![]() 层的注意力机制计算得到,
层的注意力机制计算得到,![]() 是对应的输入线性变换的权重矩阵。对于每一个结点,最后走的数据包括
是对应的输入线性变换的权重矩阵。对于每一个结点,最后走的数据包括![]() 个特征而不是
个特征而不是![]() 。
。
如果在网络的最后一层还是使用多头注意力,将矩阵串联是不明智的,最后作者选择取一个均值:
多头注意力如图1右边所示。