DW打卡第二天——朴素贝叶斯

朴素贝叶斯

相关概念（生成模型、判别模型)
先验概率、条件概率
贝叶斯决策理论
贝叶斯定理公式
极值问题情况下的每个类的分类概率
下溢问题如何解决
零概率问题如何解决？
优缺点
sklearn参数详解，Python绘制决策树

1. 相关概念

最通俗的理解，嘻嘻！
判别式模型举例：要确定一个羊是山羊还是绵羊，用判别模型的方法是从历史数据中学习到模型，然后通过提取这只羊的特征来预测出这只羊是山羊的概率，是绵羊的概率。

常见的基于判别模型算法有逻辑回归、线性回归、支持向量机、提升方法、条件随机场、人工神经网络、随机森林、感知器

生成式模型举例：利用生成模型是根据山羊的特征首先学习出一个山羊的模型，然后根据绵羊的特征学习出一个绵羊的模型，然后从这只羊中提取特征，放到山羊模型中看概率是多少，在放到绵羊模型中看概率是多少，哪个大就是哪个。

在机器学习中，生成模型可以用来直接对数据建模（例如根据某个变量的概率密度函数进行数据采样），也可以用来建立变量间的条件概率分布。条件概率分布可以由生成模型根据贝叶斯定理形成。
常见的基于生成模型算法有朴素贝叶斯分类器、高斯混合模型和其他混合模型、隐马尔可夫模型、随机上下文无关文法、AODE分类器、潜在狄利克雷分配模型、受限玻尔兹曼机

细细品味上面的例子，判别式模型是根据一只羊的特征可以直接给出这只羊的概率（比如logistic regression，这概率大于0.5时则为正例，否则为反例），而生成式模型是要都试一试，最大的概率的那个就是最后结果~

在机器学习中任务 是从属性X预测标记Y，判别模型求的是P(Y|X)，即后验概率；而生成模型最后求的是P(X,Y)，即联合概率。

从本质上来说：判别模型之所以称为“判别”模型，是因为其根据X“判别”Y；而生成模型之所以称为“生成”模型，是因为其预测的根据是联合概率P(X,Y)，而联合概率可以理解为“生成”(X,Y)样本的概率分布（或称为 依据）；具体来说，机器学习已知X，从Y的候选集合中选出一个来，可能的样本有(X,Y_1), (X,Y_2), (X,Y_3),……，(X,Y_n),实际数据是如何“生成”的依赖于P(X,Y)，那么最后的预测结果选哪一个Y呢？那就选“生成”概率最大的那个吧~

生成模型是所有变量的全概率模型，而判别模型是在给定观测变量值前提下目标变量条件概率模型。因此生成模型能够用于模拟（即生成）模型中任意变量的分布情况，而判别模型只能根据观测变量得到目标变量的采样。判别模型不对观测变量的分布建模，因此它不能够表达观测变量与目标变量之间更复杂的关系。因此，生成模型更适用于无监督的任务，如分类和聚类。

统计学习方法p28
链接：https://www.zhihu.com/question/20446337/answer/256466823

2.先验概率、条件概率

条件概率: 就是事件A在事件B发生的条件下发生的概率。条件概率表示为P（A|B），读作“A在B发生的条件下发生的概率”。

先验概率:事情发生前的预测概率。在贝叶斯统计中，某一不确定量 p 的先验概率分布是在考虑"观测数据"前，能表达 p 不确定性的概率分布。它旨在描述这个不确定量的不确定程度，而不是这个不确定量的随机性。这个不确定量可以是一个参数，或者是一个隐含变量。
后验概率: 在贝叶斯统计中，一个随机事件或者一个不确定事件的后验概率是在考虑和给出相关证据或数据后所得到的条件概率。同样，后验概率分布是一个未知量（视为随机变量）基于试验和调查后得到的概率分布。“后验”在本文中代表考虑了被测试事件的相关证据。
通过上述西瓜的数据集来看

条件概率，就是在条件为瓜的颜色是青绿的情况下，瓜是好瓜的概率

先验概率，就是常识、经验、统计学所透露出的“因”的概率，即瓜的颜色是青绿的概率。

后验概率，就是在知道“果”之后，去推测“因”的概率，也就是说，如果已经知道瓜是好瓜，那么瓜的颜色是青绿的概率是多少。后验和先验的关系就需要运用贝叶斯决策理论来求解。

3. 贝叶斯决策理论

参考dw机器学习基础之朴素贝叶斯

4. 贝叶斯公式

关于最大似然估计，请参考我的这篇博客，里面有极大似然的深刻理解。https://blog.csdn.net/CSDNccfcsp/article/details/105626684










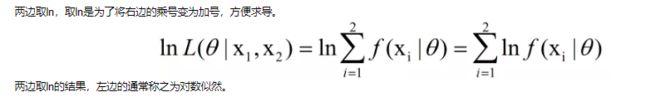
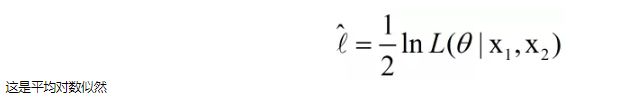
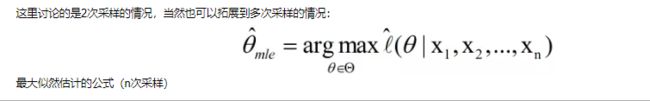
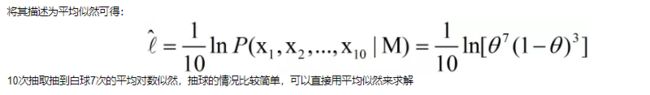
贝叶斯分类器的训练过程就是参数估计。总结最大似然法估计参数的过程，一般分为以下四个步骤：

1.写出似然函数；
2.对似然函数取对数，并整理；
3.求导数，令偏导数为0，得到似然方程组；
4.解似然方程组，得到所有参数即为所求。

朴素贝叶斯分类器
插播一条：判别式是直接对后验概率建模，但是生成模型通过贝叶斯定理这一“桥梁”使问题转化为求联合概率
之所以称为朴素贝叶斯，是因为它假设每个输入变量是独立的。这是一个强硬的假设，实际情况并不一定，但是这项技术对于绝大部分的复杂问题仍然非常有效。
朴素贝叶斯模型由两种类型的概率组成：

每个类别的概率P(Cj)；
每个属性的条件概率P(Ai|Cj)。
假设我有 7 个棋子，其中 3 个是白色的，4 个是黑色的。那么棋子是白色的概率就是 3/7，黑色的概率就是 4/7，这个就是类别概率。

假设我把这 7 个棋子放到了两个盒子里，其中盒子 A 里面有 2 个白棋，2 个黑棋；盒子 B 里面有 1 个白棋，2 个黑棋。那么在盒子 A 中抓到白棋的概率就是 1/2，抓到黑棋的概率也是 1/2，这个就是条件概率，也就是在某个条件（比如在盒子 A 中）下的概率。

假设，我取出来的是白色的棋子，我问，属于A盒子的概率？ 你会算吗？

为了训练朴素贝叶斯模型，我们需要先给出训练数据，以及这些数据对应的分类。那么上面这两个概率，也就是类别概率和条件概率。他们都可以从给出的训练数据中计算出来。一旦计算出来，概率模型就可以使用贝叶斯原理对新数据进行预测。

原文链接：https://blog.csdn.net/wuzhongqiang/article/details/104268837

5. 极值问题情况下的每个类的分类概率

极值问题

很多时候遇到求出各种目标函数（object function）的最值问题（最大值或者最小值）。关于函数最值问题，其实在高中的时候我们就已经了解不少，最经典的方法就是：直接求出极值点。这些极值点的梯度为0。若极值点唯一，则这个点就是代入函数得出的就是最值；若极值点不唯一，那么这些点中，必定存在最小值或者最大值（去除函数的左右的最端点），所以把极值代入函数，经对比后可得到结果。

请注意：并不一定所有函数的极值都可以通过设置导数为0的方式求 出。也就是说，有些问题中当我们设定导数为0时，未必能直接计算出满足导数为0的点（比如逻辑回归模型），这时候就需要利用数值计算相关的技术（最典型为梯度下降法，牛顿法……）。

6. 下溢问题如何解决

数值下溢问题：是指计算机浮点数计算的结果小于可以表示的最小数，因为计算机的能力有限，当数值小于一定数时，其无法精确保存，会造成数值的精度丢失，由上述公式可以看到，求概率时多个概率值相乘，得到的结果往往非常小；因此通常采用取对数的方式，将连乘转化为连加，以避免数值下溢。

所谓拉普拉斯平滑，是为了防止其他属性携带的信息被训练集中某个分类下未出现的属性值“抹去”，造成预测出来的概率绝对为0。对应方法：对先验概率（类别概率）的分子+1，分母加上总类别数;对条件概率的分子+1，分母加上对应特征的可能取值类别数。计算之后代入到贝叶斯公式中。

8. sklearn参数详解

sklearn接口

from sklearn.naive_bayes import GaussianNB#高斯朴素贝叶斯 特征变量是连续变量，符合高斯分布，比如说人的身高，物体的长度

from sklearn.datasets import load_iris
import pandas as pd
from sklearn.model_selection import train_test_split
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2)
clf = GaussianNB().fit(X_train, y_train)
print ("Classifier Score:", clf.score(X_test, y_test))

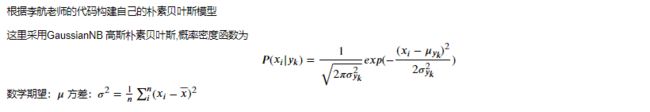
https://github.com/fengdu78/lihang-code/blob/master/%E7%AC%AC04%E7%AB%A0%20%E6%9C%B4%E7%B4%A0%E8%B4%9D%E5%8F%B6%E6%96%AF/4.NaiveBayes.ipynb

手撸NB:

import math
class NaiveBayes:
	def __init__(self):
		self.model=None
	#数学期望
	def mean(X):
		"""计算均值
        Param: X : list or np.ndarray
        
        Return:
            avg : float
        
        """
        avg = 0.0
        #   /表示浮点数除法，返回浮点结果 //整数除法
        # ========= show me your code ==================
        avg = sum(X) / float(len(X))
        # ========= show me your code ==================
        return avg
    def stdev(self,X):
       	"""计算标准差
        Param: X : list or np.ndarray
        
        Return:
            res : float
        
        """
        res = 0.0
        # ========= show me your code ==================
        avg = self.mean(X)
        res = math.sqrt(sum([pow(x - avg, 2) for x in X]) / float(len(X)))
        # ========= show me your code ==================
        return res
    def gaussian_probability(self, x, mean, stdev):
     	"""根据均值和标注差计算x符合该高斯分布的概率
        Parameters:
        ----------
        x : 输入
        mean : 均值
        stdev : 标准差
        
        Return:
        
        res : float， x符合的概率值
            
        """
    	res=0.0
    	exponent=math.exp(-(math.pow(x-mean,2)/(2*math.pow(stdev,2))))
       	res=(1/(math.sqrt(2*math.pi)*stdev))*exponent
       	return res
    # 处理X_train
    def summarize(self, train_data):
        """计算每个类目下对应数据的均值和标准差
        Param: train_data : list
        
        Return : [mean, stdev]
        """
        summaries = [0.0, 0.0]
        # ========= show me your code ==================就是为了每一列求均值
        summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]
        
        # ========= show me your code ==================
        return summaries

    # 分类别求出数学期望和标准差
    def fit(self, X, y):
        labels = list(set(y))
        data = {label: [] for label in labels}
        for f, label in zip(X, y):
            data[label].append(f)
        self.model = {
            label: self.summarize(value) for label, value in data.items()
        }
        return 'gaussianNB train done!'

    # 计算概率
    def calculate_probabilities(self, input_data):
        """计算数据在各个高斯分布下的概率
        Paramter:
        input_data : 输入数据
        
        Return:
        probabilities : {label : p}
        """
        # summaries:{0.0: [(5.0, 0.37),(3.42, 0.40)],    1.0: [(5.8, 0.449),(2.7, 0.27)]}
        # input_data:[1.1, 2.2]
        probabilities = {}
        # ========= show me your code ==================
        for label, value in self.model.items():
            probabilities[label] = 1#对应高斯分布下概率和为1
            for i in range(len(value)):
                mean, stdev = value[i]
                probabilities[label] *= self.gaussian_probability(
                    input_data[i], mean, stdev)
        # ========= show me your code ==================
        return probabilities

    # 类别
    def predict(self, X_test):
        # {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
        label = sorted(self.calculate_probabilities(X_test).items(), key=lambda x: x[-1])[-1][0]
        return label
    # 计算得分
    def score(self, X_test, y_test):
        right = 0
        for X, y in zip(X_test, y_test):
            label = self.predict(X)
            if label == y:
                right += 1

        return right / float(len(X_test))

model = NaiveBayes()
model.fit(X_train, y_train)
print(model.predict([4.4,  3.2,  1.3,  0.2]))
model.score(X_test, y_test)

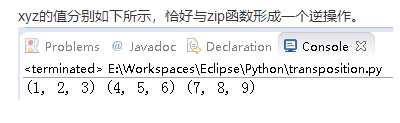
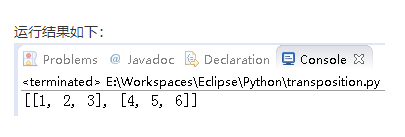
zip(*)
https://blog.csdn.net/yongh701/article/details/50283689
比如下述的一段代码：

#-*-coding:utf-8-*-
x=[1,2,3];
y=[4,5,6];
z=[7,8,9];
print zip(x,y,z)

意思是取各个list的第x项，作为返回的二维数组的第x项中的一维数组中的元素。
其实zip还是反过来会这个二维数组操作，但要注意写成zip(*)，表示这是一个zip的逆操作。

比如下述的一段代码：

# -*-coding:utf-8-*-
array=[[1,4,7],[2,5,8],[3,6,9]];
x,y,z=zip(*array);
print x,y,z;

因此对于一个数组的转置，代码如下：

# -*-coding:utf-8-*-
array = [[1, 4], [2, 5], [3, 6]];
print map(list, zip(*array));

9.优缺点

优点

• 朴素贝叶斯模型有稳定的分类效率。
• 对小规模的数据表现很好，能处理多分类任务，适合增量式训练，尤其是数据量超出内存时，可以一批批的去增量训练。
• 对缺失数据不太敏感，算法也比较简单，常用于文本分类。

缺点:

• 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
• 需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
• 由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
• 对输入数据的表达形式很敏感。

10. 参考文献
    西瓜书 https://samanthachen.github.io/2016/08/05/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0_%E5%91%A8%E5%BF%97%E5%8D%8E_%E7%AC%94%E8%AE%B07/

https://www.jianshu.com/p/f1d3906e4a3e

https://zhuanlan.zhihu.com/p/66117273

https://zhuanlan.zhihu.com/p/39780650

https://blog.csdn.net/zrh_CSDN/article/details/81007851