线性分类（五）-- 朴素贝叶斯法

        贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。贝叶斯分类法是统计学分类方法，它可以预测类隶属关系的概率，如一个给定元组属于一个特定类的概率。而朴素贝叶斯分类是贝叶斯分类中最简单，也是最常见的一种分类方法。此外，朴素贝叶斯算法仍然是流行的十大挖掘算法之一，该算法是有监督的学习算法，解决的是分类问题。该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。但由于该算法以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提(这个假设在实际应用中往往是不成立的)，就会导致算法精度在某种程度上受影响。

        上一节的高斯判别分析的是对数据集的分布作出了高斯分布的假设，同时引入伯努利分布作为类先验，从而利用最大后验求得这些假设中的参数。朴素贝叶斯对数据的属性之间的关系作出了假设，一般地，我们需要得到 $P(x\text{x}x|y)$ 这个概率值，由于 $x\text{x}x$ 有 $p$ 个维度，因此需要对这么多的维度的联合概率进行采样，但是我们知道这么高维度的空间中采样需要的样本数量非常大才能获得较为准确的概率近似。

        在一般的有向概率图模型中，对各个属性维度之间的条件独立关系作出了不同的假设，其中最为简单的一个假设就是在朴素贝叶斯模型描述中的条件独立性假设，即假定一个属性值在给定类上的概率独立于其他属性的值，这一假定称为类条件独立性。朴素贝叶斯是基于贝叶斯定理与特征之间条件独立这个假设的分类方法，属于生成模型。

        最为广泛的两种分类模型是决策树（Decision Tree Model）和朴素贝叶斯模型（Naive Bayesian Model，NBM）。和决策树模型相比，朴素贝叶斯分类器（Naive Bayes Classifier 或 NBC）发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率。同时，NBC模型所需估计的参数很少，对缺失数据不太敏感，算法也比较简单。理论上，NBC模型与其他分类方法相比具有最小的误差率。

1 朴素贝叶斯

1.1 贝叶斯定理

        $P(A|B)$ 表示事件 $B$ 已经发生的前提下，事件 $A$ 发生的概率，叫做事件 $B$ 发生下事件 $A$ 的条件概率。其基本求解公式为：
$$P(A|B)=\frac{P(AB)}{P(B)}\text{\hspace{1em}(1.1)}$$
        贝叶斯定理之所以有用，是因为我们在生活中经常遇到这种情况：我们可以很容易直接得出 $P(A|B)$，$P(B|A)$ 则很难直接得出，但我们更关心 $P(B|A)$，贝叶斯定理就为我们打通从 $P(A|B)$ 获得 $P(B|A)$ 的道路。 下面这里直接给出贝叶斯定理的公式：
$$P(B|A)=\frac{P(A|B)P(B)}{P(A)}\text{\hspace{1em}(1.2)}$$
        其中 $P(B\mid A)$ 则表示在 $A$ 发生的情况下 $B$ 发生的概率。
        当特征条件独立时，则可以写为：
$$P\left(类别|特征\right)=\frac{P(特征|类别)P(类别)}{P(特征)}\text{\hspace{1em}(1.3)}$$

1.2 朴素贝叶斯分类的原理与流程

        训练数据集：$T=\left\{\left({x\text{x}x}_1,y_1\right),\left({x\text{x}x}_2,y_2\right),\cdots ,\left({x\text{x}x}_N,y_N\right)\right\}$，其中 ${x\text{x}x}_i\in \mathcal{X}\subseteq R^p,y_i\in \mathcal{Y}=\left\{c_1,c_2,\cdots ,c_K\right\},i=1,2,\cdots ,N$，${x\text{x}x}_i$ 为第 $i$ 个特征向量（实例）， $y_i$ 为 ${x\text{x}x}_i$ 的类标记， $X\text{X}X$ 是定义在输入空间 $\mathcal{X}$ 上的随机向量， $Y$ 是定义在输出空间 $\mathcal{Y}$ 上的随机变量。$X^{(j)},j=1,2,\cdots ,p$ 表示第 $j$ 个特征变量，$X\text{X}X=[X^{(1)},X^{(2)},\cdots ,X^{(p)}]$。$P\left(X,Y\right)$ 是 $X$ 和 $Y$ 的联合概率分布。

        朴素贝叶斯法通过训练集学习到联合概率分布 $P\left(X,Y\right)$。先验概率分布为 $P(Y=c_k),k=1,2,...,K$ 和条件概率分布 $P(X\text{X}X=x\text{x}x|Y=c_k)=P(X^{(1)}=x^{(1)},\cdots ,X^{(p)}=x^{(p)}|Y=c_k),k=1,2,\cdots ,K$

        由于朴素贝叶斯算法对条件概率分布作了条件独立性假设，故
$$\begin{array}{rl}P(X=x\text{x}x|Y=c_k)& =P(X^{(1)}=x^{(1)},\cdots ,X^{(p)}=x^{(p)}|Y=c_k)\\ & =\prod _{j=1}^{p}P(X^{(j)}=x^{(j)}|Y=c_k)\end{array}\text{\hspace{1em}(1.4)}$$
        即用于分类的特征在类确定的条件下都是条件独立的。
        由条件概率公式可得：
$$\begin{array}{rl}& \\ & P\left(X\text{X}X=x\text{x}x,Y=c_k\right)=P\left(X\text{X}X=x\text{x}x|Y=c_k\right)P\left(Y=c_k\right)\\ & P\left(X\text{X}X=x\text{x}x,Y=c_k\right)=P\left(Y=c_k|X\text{X}X=x\text{x}x\right)P\left(X\text{X}X=x\text{x}x\right)\end{array}\text{\hspace{1em}(1.5)}$$

        于是得到朴素贝叶斯算法的基本形式：
$$\begin{array}{rl}& \\ & P\left(\mathbf{X}=\mathbf{x}|Y=c_k\right)P\left(Y=c_k\right)=P\left(Y=c_k|\mathbf{X}=\mathbf{x}\right)P\left(\mathbf{X}=\mathbf{x}\right)\\ & P\left(Y=c_k|\mathbf{X}=\mathbf{x}\right)=\frac{P\left(\mathbf{X}=\mathbf{x}|Y=c_k\right)P\left(Y=c_k\right)}{P\left(\mathbf{X}=\mathbf{x}\right)}\\ & =\frac{P\left(\mathbf{X}=\mathbf{x}|Y=c_k\right)P\left(Y=c_k\right)}{{\sum }_{Y}P\left(\mathbf{X}=\mathbf{x},Y=c_k\right)}\\ & =\frac{P\left(\mathbf{X}=\mathbf{x}|Y=c_k\right)P\left(Y=c_k\right)}{{\sum }_{Y}P\left(\mathbf{X}=\mathbf{x}|Y=c_k\right)P\left(Y=c_k\right)}\\ & =\frac{P\left(Y=c_k\right){\prod }_{j=1}^{p}P\left(X^{(j)}=x^{(j)}|Y=c_k\right)}{{\sum }_{Y}P\left(Y=c_k\right){\prod }_{j=1}^{p}P\left(X^{(j)}=x^{(j)}|Y=c_k\right)}\end{array}\text{\hspace{1em}(1.6)}$$
        朴素贝叶斯分类器可表示为
$$\begin{array}{rl}& \\ & y=f\left(x\right)=\arg \underset{c_k}{\max }\frac{P\left(Y=c_k\right){\prod }_{j=1}^{p}P\left(X^{(j)}=x^{(j)}|Y=c_k\right)}{{\sum }_{Y}P\left(Y=c_k\right){\prod }_{j=1}^{p}P\left(X^{(j)}=x^{(j)}|Y=c_k\right)}\\ & =\arg \underset{c_k}{\max }P\left(Y=c_k\right)\prod _{j=1}^{p}P\left(X^{(j)}=x^{(j)}|Y=c_k\right)\end{array}\text{\hspace{1em}(1.7)}$$

        因为对于每一个类别 $c_k$，分母 ${\sum }_{Y}P\left(Y=c_k\right){\prod }_{j=1}^{p}P\left(X^{(j)}=x^{(j)}|Y=c_k\right)$的值都是相同的。

        朴素贝叶斯分类时对给定的输入${x\text{x}x}_i$，通过学习到的模型计算后验概率分布 $P\left(Y=c_k\right){\prod }_{j=1}^{p}P\left(X_i^{(j)}=x_i^{(j)}|Y=c_k\right)$，将后验概率最大的类作为 ${x\text{x}x}_i$ 的所属类别输出。

        不想看上面公式的，可以看这篇文章用了四个例子简单介绍了贝叶斯的核心思想——非常通俗的朴素贝叶斯算法（Naive Bayes）

1.3 后验概率最大化的含义

        后验概率最大化原则等价于期望风险最小化原则。
        假设选择0-1损失函数：
$$L(Y,f(X\text{X}X))=\{\begin{array}{c}1,Y\ne f(X\text{X}X)\\ 0,Y=f(X\text{X}X)\end{array}\text{\hspace{1em}(1.8)}$$
        式中 $f(X\text{X}X)$ 是分类决策函数，这时期望风险函数为：

$$\begin{array}{rl}{R}_{exp}(f)& =E[L(Y,f(X\text{X}X))]\\ & =\iint L(Y=y,f(X\text{X}X=x\text{x}x))P(X\text{X}X=x\text{x}x,Y=y)dx\text{x}xdy\\ & =\iint L(Y=y,f(X\text{X}X=x\text{x}x))P(Y=y|X\text{X}X=x\text{x}x)P(X\text{X}X=x\text{x}x)dx\text{x}xdy\\ & =\int \left\{\int \left[L(Y=y,f(X\text{X}X=x\text{x}x))P(Y=y|X\text{X}X=x\text{x}x)\right]dy\right\}p(X\text{X}X=x\text{x}x)dx\text{x}x\\ & =\int \left\{\sum _{k=1}^{K}L(c_k,f(X\text{X}X=x\text{x}x))P(c_k|X\text{X}X=x\text{x}x)\right\}p(X\text{X}X=x\text{x}x)\\ & =E_{\mathbf{X}}\left[\sum _{k=1}^{K}L(c_k,f(X\text{X}X))P(c_k|X\text{X}X)\right]\end{array}\text{\hspace{1em}(1.9)}$$

        为了使期望风险最小化，只需对 $X=x\text{x}x$ 逐个极小化，由此得到：

$$\begin{array}{rl}f(x\text{x}x)& =arg\underset{y\in y}{\min }\sum _{k=1}^{K}L(c_k,y)P(c_k|X\text{X}X=x\text{x}x)\\ & =arg\underset{y\in y}{\min }\sum _{k=1}^{K}P(y\ne c_k|X\text{X}X=x\text{x}x)\\ & =arg\underset{y\in y}{\min }(1-P(y=c_k|X\text{X}X=x\text{x}x))\\ & =arg\underset{y\in y}{\max }P(y=c_k|X\text{X}X=x\text{x}x))\end{array}\text{\hspace{1em}(1.10)}$$

        这样一来，根据期望风险最小化准则就得到了后验概率最大化准则：
$$f(x\text{x}x)=arg\underset{y\in y}{\max }P(y=c_k|X\text{X}X=x\text{x}x))\text{\hspace{1em}(1.11)}$$
        这个就是朴素贝叶斯法所采用的原理，我们只要计算出所有的 $k$ 个条件概率 $P(y=c_k|X\text{X}X=x\text{x}x))$，然后找出最大的条件概率对应的类别，这就是朴素贝叶斯的预测了。

2 参数估计

        对于 $P(Y=c_k)$ 比较简单，通过最大似然估计我们很容易得到 $P(Y=c_k)$ 为样本类别 $c_k$ 出现的频率，即样本类别 $c_k$ 出现的次数除以样本总数 $N$。即
$$\begin{array}{rl}& \\ & P\left(Y=c_k\right)=\frac{{\sum }_{i=1}^{N}I\left(y_i=c_k\right)}{N}k=1,2,\cdots ,K\end{array}\text{\hspace{1em}(2.1)}$$

        对于 $P\left(X^{(j)}=x^{(j)}|Y=c_k\right)$，这个取决于我们的先验条件。

2.1 多项式朴素贝叶斯

        如果 $X^{(j)}$ 是离散的值，可能取值的集合为 $\left\{a_{j1},a_{j2},\cdots ,a_{j{S}_j}\right\}$ ，同时我们可以假设 $X^{(j)}$ 服从多项式分布，这样得到 $P\left(X^{(j)}=a_{jl}|Y=c_k\right),l=1,2,\cdots ,S_j$ 是在样本类别 $c_k$ 中，特征 $X^{(j)}=a_{jl}$ 出现的频率。即：

$$\begin{array}{rl}P\left(X^{(j)}=a_{jl}|Y=c_k\right)& ＝\frac{{\sum }_{i=1}^{N}I\left({x\text{x}x}_i^{(j)}=a_{jl},y_i=c_k\right)}{{\sum }_{i=1}^{N}I\left(y_i=c_k\right)}\\ & j=1,2,\cdots ,p;l=1,2,\cdots ,S_j;k=1,2,\cdots ,K\end{array}\text{\hspace{1em}(2.2)}$$

        其中，$x_i^{(j)}$ 是第 $i$ 个样本的第 $j$ 个特征；$a_{jl}$ 是第 $j$ 个特征可能取的第 $l$ 个值；$I$ 是指示函数。

        用极大似然估计可能会出现所要估计的概率值为0的情况（如可能某些特征在某些类别中没有出现），这时会影响到后验概率的计算结果，使分类产生误差，解决这一问题的方法是采用贝叶斯估计。 条件概率的贝叶斯估计：
$$\begin{array}{rl}& \\ & P_{\lambda }\left(X^{(j)}=a_{jl}|Y=c_k\right)＝\frac{{\sum }_{i=1}^{N}I\left({\mathbf{x}}_i^{(j)}=a_{jl},y_i=c_k\right)+\lambda }{{\sum }_{i=1}^{N}I\left(y_i=c_k\right)+S_j\lambda }\end{array}\text{\hspace{1em}(2.3)}$$

        式中 $\lambda \ge 0$。当 $\lambda =0$ 时，是极大似然估计；当 $\lambda =1$ 时，称为拉普拉斯平滑。
        此时先验概率的贝叶斯估计为：
$$\begin{array}{rl}& \\ & P\left(Y=c_k\right)=\frac{{\sum }_{i=1}^{N}I\left(y_i=c_k\right)+\lambda }{N+K\lambda }\end{array}\text{\hspace{1em}(2.4)}$$

2.2 伯努利朴素贝叶斯

        如果 $X^{(j)}$ 是非常稀疏的离散值，即各个特征出现概率很低，这时我们可以假设 $X^{(j)}$ 服从伯努利分布，即特征 $X^{(j)}$ 出现记为1，不出现记为0，$X^{(j)}$ 取值的集合为 $\{0,1\}$。即只要 $X^{(j)}$ 出现即可，我们不关注 $X^{(j)}$ 的次数。这样得到 $P\left(X^{(j)}=x^{(j)}|Y=c_k\right)$ 是在样本类别 $c_k$ 中，$X^{(j)}$ 出现的频率。此时有：

$$P(X^{(j)}=x^{(j)}|Y=c_k)=P(x^{(j)}=1|Y=C_k)x^{(j)}+(1-P(x^{(j)}=1|Y=C_k))(1-x^{(j)})\text{\hspace{1em}(2.5)}$$

2.3 高斯朴素贝叶斯

        如果 $X^{(j)}$ 是连续值，我们通常取 $X^{(j)}$ 的先验概率为正态分布，即在样本类别 $C_k$ 中，$X^{(j)}$ 的值服从正态分布。这样 $P\left(X^{(j)}=x^{(j)}|Y=c_k\right)$ 的概率分布是：
$$P\left(X^{(j)}=x^{(j)}|Y=c_k\right)=\frac{1}{\sqrt{2\pi {\sigma }_k^2}}exp(-\frac{(x^{(j)}-{\mu }_k{)}^2}{2{\sigma }_k^2})\text{\hspace{1em}(2.6)}$$

        其中 ${\mu }_k$ 和 ${\sigma }_k^2$ 是正态分布的期望和方差，可以通过极大似然估计求得。${\mu }_k$ 为在样本类别 $c_k$ 中，所有 $X^{(j)}$ 的平均值。${\sigma }_k^2$ 为在样本类别 $c_k$ 中，所有 $X^{(j)}$ 的方差。对于一个连续的样本值，带入正态分布的公式，就可以求出概率分布了。

        针对参数的求解方法不同，这里简单介绍了常见的三种朴素贝叶斯类型：伯努利朴素贝叶斯，多项式朴素贝叶斯和高斯朴素贝叶斯。不同类型的朴素贝叶斯对参数的求法不同，而根源在于对 $P\left(X^{(j)}=x^{(j)}|Y=c_k\right)$ 的假设分布不同，也就是说在给定类别的情况下，对 $X^{(j)}$ 假设的分布不同：伯努利假设是伯努利分布（其实应该是多变量伯努利分布），多项式假设是多项式分布，而高斯也就是假设是高斯分布（其实是多变量高斯分布）。然后，我们细化到三种不同类型的朴素贝叶斯理论中。更多内容，请阅读：朴素贝叶斯以及三种常见模型推导

---

3 朴素贝叶斯算法流程

        输入：线性可分训练数据集 $T=\left\{\left({x\text{x}x}_1,y_1\right),\left({x\text{x}x}_2,y_2\right),\cdots ,\left({x\text{x}x}_N,y_N\right)\right\}$，其中 ${x\text{x}x}_i=[x_i^{(1)},x_i^{(2)},\cdots ,x_i^{(n)}{]}^T$，$x_i^{(j)}$ 是第 $i$ 个样本的第 $j$ 个特征，$x_i^{(j)}\in \left\{a_{j1},a_{j2},\cdots ,a_{j{S}_j}\right\}$，$a_{jl}$ 是第 $j$ 个特征可能取的第 $l$ 个值，$j=1,2,\cdots ,p；l=1,2,\cdots ,S_j$， $y_i\in \left\{c_1,c_2,\cdots ,c_K\right\}$，实例 $x\text{x}x$ 输出：实例 $x\text{x}x$ 的分类
算法流程如下：

（1）如果没有 $Y$ 的先验概率，则计算 $Y$ 的 $K$ 个先验概率：
$$\begin{array}{rl}& \\ & P\left(Y=c_k\right)=\frac{{\sum }_{i=1}^{N}I\left(y_i=c_k\right)+\lambda }{N+K\lambda }\end{array}$$
（2）分别计算第 $k$ 个类别的第 $j$ 维特征的第 $l$ 个取值条件概率：$P\left(X^{(j)}=a_{jl}|Y=c_k\right)$

a）如果是离散值：
$$\begin{array}{rl}& \\ & P_{\lambda }\left(X^{(j)}=a_{jl}|Y=c_k\right)＝\frac{{\sum }_{i=1}^{N}I\left({\mathbf{x}}_i^{(j)}=a_{jl},y_i=c_k\right)+\lambda }{{\sum }_{i=1}^{N}I\left(y_i=c_k\right)+S_j\lambda }\end{array}$$ $\lambda$ 可以取值为1，或者其他大于0的数字。

b）如果是稀疏二项离散值：
$$P(X^{(j)}=x^{(j)}|Y=c_k)=P(x^{(j)}=1|Y=C_k)x^{(j)}+(1-P(x^{(j)}=1|Y=C_k))(1-x^{(j)})$$ 此时 $X^{(j)}$ 只有0和1两种取值。
c）如果是连续值不需要计算各个$l$ 的取值概率，直接求正态分布的参数：
$$P\left(X^{(j)}=x^{(j)}|Y=c_k\right)=\frac{1}{\sqrt{2\pi {\sigma }_k^2}}exp(-\frac{(x^{(j)}-{\mu }_k{)}^2}{2{\sigma }_k^2})$$ 其中 ${\mu }_k$ 和 ${\sigma }_k^2$ 是正态分布的期望和方差，需要通过极大似然估计求得。${\mu }_k$ 为在样本类别 $c_k$ 中，所有 $X^{(j)}$ 的平均值。${\sigma }_k^2$ 为在样本类别 $c_k$ 中，所有 $X^{(j)}$ 的方差。

（3）对于实例 $x\text{x}x$，分别计算： $$P\left(Y=c_k\right)\prod _{j=1}^{p}P\left(X^{(j)}=x^{(j)}|Y=c_k\right),k=1,2,\cdots ,K$$
（4）确定实例 $x\text{x}x$ 的分类Cresult $$y=\arg \underset{c_k}{\max }P\left(Y=c_k\right)\prod _{j=1}^{p}P\left(X^{(j)}=x^{(j)}|Y=c_k\right)$$

---

4 半朴素贝叶斯

        为了降低贝叶斯公式中估计后验概率 $P(c|x\text{x}x)$ 的困难，朴素贝叶斯分类器采用了属性条件独立性假设，但在现实任务中这个假设往往很难成立，因为往往属性之间包含着各种依赖。 于是，人们尝试对这个假设进行一定程度的放松，由此产生了“半朴素贝叶斯分类器”（semi-naive Bayes classifiers）的学习方法。

        半朴素贝叶斯分类器的基本想法是适当考虑一部分属性间的相互依赖信息，从而既不需进行完全联合概率计算，又不至于彻底忽略了比较强的属性依赖关系。独依赖估计（One-Dependent Estimator，简称ODE）是半朴素贝叶斯分类器最常用的一种策略。顾名思义，独依赖是假设每个属性在类别之外最多依赖一个其他属性，即
$$\begin{array}{r}P(c|x\text{x}x)\propto P(c)\prod _{j=1}^{p}P(x^{(j)}|c,p{a}^{(j)})\end{array}\text{\hspace{1em}(4.1)}$$
        其中，$p{a}^{(j)}$ 为属性 $x^{(j)}$ 所依赖的属性，称为 $x^{(j)}$ 的父属性。假设父属性 $p{a}^{(j)}$ 已知，那么可以使用下面的公式估计 $P(x^{(j)}|c,p{a}^{(j)})$
$$P(x^{(j)}|c,p{a}^{(j)})=\frac{P(x^{(j)},c,p{a}^{(j)})}{P(c,p{a}^{(j)})}\text{\hspace{1em}(4.2)}$$

        于是，问题的关键变成了如何确定每个属性的父属性。不同的做法产生了不同的独依赖分类器。

• SPODE（Super-Parent ODE）假设所有的属性都依赖于同一个属性，称为超父。
• TAN（Tree Augmented naive Bayes）则在最大带权生成树算法的基础上发展的一种方法。
• AODE（Averaged ODE）是一种基于集成学习机制、更为强大的独依赖分类器。

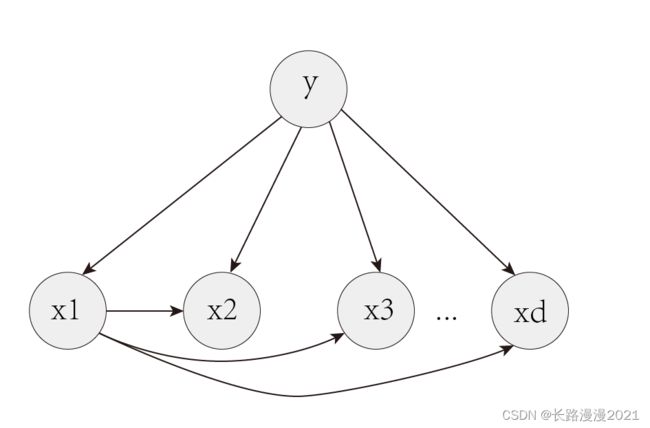
4.1 SPODE（Super-Parent ODE）

        假设所有属性都依赖于同一个属性（超父， super-parent），然后通过交叉验证确定超父。

4.2 TAN（Tree Augmented Naive Bayes）

        在最大带权生成树算法的基础上，通过某种规则生成一个树，树的结构与生成的规则分别为：

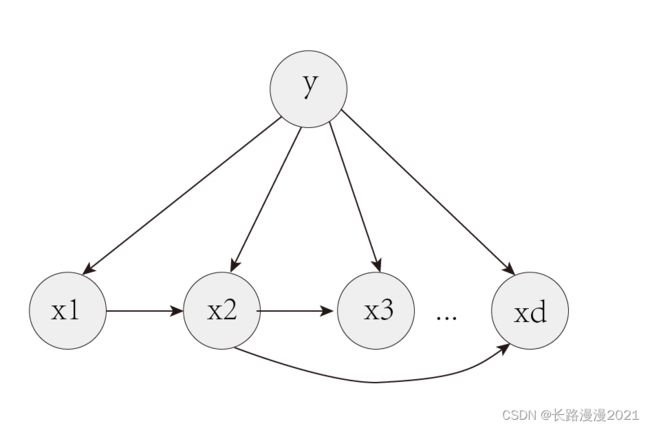
        TAN的实施步骤如下：

1. 计算任意属性之间的条件互信息
   $$I(x^{(i)},x^{(j)}|y)=\sum _{x^{(i)},x^{(j)};c_k\in Y}P(x^{(i)},x^{(j)}|c_k)\log \frac{P(x^{(i)},x^{(j)}|c_k)}{P(x^{(i)}|c_k)P(x^{(j)}|c_k)}\text{\hspace{1em}(4.3)}$$

2. 以属性为节点构建完全图，任意两个节点之间边的权重设为 $I(x^{(i)},x^{(j)}|y)$；

3. 构建此完全图的最大带权生成树，挑选根变量，将边置为有向；

4. 加入类别结点 $y$，增加从 $y$ 到每个属性的有向边。

        条件互信息 $I(x^{(i)},x^{(j)}|y)$ 刻画了属性 $x^{(i)}$ 和 $x^{(j)}$ 在已知类别情况下的相关性。因此，通过最大生成树算法，TAN实际上仅保留了强相关属性之间的依赖性。

        TAN 代码实现，可以参考：Python版 半朴素贝叶斯-进阶（SPODE与TAN）

4.3 AODE（Averaged ODE）

        与SPODE通过模型选择确定超父属性不同，AODE将每个属性作为超父来构建SPODE，然后将那些具有足够训练数据支撑的SPODE集成起来作为最终结果，即
$$P(c\mid x)\propto \sum _{{i=1}_{|D_{x^{(i)}}|\ge m^{\prime }}}^{p}P(c,x^{(i)}){\Pi }_{j=1}^{d}P(x^{(j)}\mid c,x^{(i)})\text{\hspace{1em}(4.4)}$$

        其中 $D_{x^{(i)}}$ 在第 $i$ 个属性上取值为 $x^{(i)}$ 的样本的集合，$m\prime$ 为阈值或者常数，显然AODE需要估计 $P(c,x^{(i)})$ 和 $P(x^{(j)}\mid c,x^{(i)})$ 于是：
$$\begin{array}{r}\hat{P}(c,x^{(i)})=\frac{|D_{c,x^{(i)}}|+1}{|D|+N_i}\\ \hat{P}(x^{(j)}\mid c,x^{(i)})=\frac{|D_{c,x^{(i)},x^{(j)}}|+1}{|D_{c,x^{(i)}}|+N_j}\end{array}\text{\hspace{1em}(4.5)}$$
        其中 $N_i$ 是第 $i$ 个属性可能的取值数，$Dc,x^{(i)}$ 是类别为 $c$ 且在第 $i$ 个属性上取值为 $x^{(i)}$ 的样本的集合， $D_{c,x^{(i)},x^{(j)}}$ 是类别为 $c$ 且在第 $i$ 和第 $j$ 个属性上取值分别为 $x^{(i)}$ 和 $x^{(j)}$ 的样本的集合。

半朴素贝叶斯分类器与贝叶斯网络的区别？
        贝叶斯网（Bayesian network）亦称“信念网”，它借助有向无环图（Directed Acyclic Graph,简称DAG）来刻画属性间的依赖关系，并使用条件概率表（Conditional Probability Table,简称CPT）来描述属性的联合概率分布。半朴素贝叶斯分类器中常用“独依赖估计”的策略，而贝叶斯网则表示能力更强，可以表示属性间的多依赖关系。贝叶斯分类器最终的目标是实现分类，而到了贝叶斯网络，目标变成了推断。了解更多，请阅读——从贝叶斯方法谈到贝叶斯网络

---

5 应用分析

        这部分内容主要参考自：机器学习–用朴素贝叶斯分类法辨别男女声音，完整代码：https://gitee.com/beiyan/machine_learning/tree/master/naive_bayes

5.1 数据集选择及处理

        Kaggle是一个提供机器学习竞赛、托管数据库、编写和分享代码的平台，上面有一些用户分享的开放数据集，本文选取Kory Becker提供的男女声音特征分类数据集：https://www.kaggle.com/primaryobjects/voicegender
        该数据集样例如下：

        这里的数据集是针对男女声音使用声波和调谐器包进行预处理，是基于声音和语音的声学特性而创建的，用来识别男性或女性的声音。我们不必过于纠结20个比较专业的的特征名称，这里把其当做一般的连续性数值特征就可以了。这里只展示了前两条数据，前20列（meanfreq, sd, median…dfrange, modindx）为声音的各种特征 ，最后一列 label 为声音的分类。我们可以看到 mode 和 dfrange 等列都有为0 的值，说明数据可能有缺失，我们在处理数据集时要考虑到数据缺失的问题.。

1. 处理缺失数据
        我们将值为 0 的特征值视为缺失，弥补缺失的办法是用该特征的平均值填充。

# 求每一个特征的平均值
data_mat = np.array(data_mat).astype(float)
count_vector = np.count_nonzero(data_mat, axis=0)
sum_vector = np.sum(data_mat, axis=0)
mean_vector = sum_vector / count_vector

# 数据缺失的地方 用 平均值填充
for row in range(len(data_mat)):
	for col in range(num):
		if data_mat[row][col] == 0.0:
			data_mat[row][col] = mean_vector[col]

2. 数据离散化
        贝叶斯公式适合标称型数据，这里每个特征都是连续的浮点数值，我们需要将特征值离散化。

        离散的方法如下：
$$F(i)=Floor(\frac{F(i)-min}{(max-min)/n})$$

        式中，$max$ 和 $min$ 分别为该特征的最大值和最小值，$n$ 为离散的程度，$Floor()$ 为向下取整。

        本文中 $n$ 取 10 ，每个特征的值离散为 $[0，1，2，3，4，5，6，7，8，9]$ 中的一个，离散化后的数据样例如下：

实现如下：

# 将数据连续型的特征值离散化处理
min_vector = data_mat.min(axis=0)
max_vector = data_mat.max(axis=0)
diff_vector = max_vector - min_vector
diff_vector /= 9

new_data_set = []
for i in range(len(data_mat)):
	line = np.array((data_mat[i] - min_vector) / diff_vector).astype(int)
    new_data_set.append(line)

3. 切分训练、测试数据集
        本数据集公有3168条数据，为了让男性声音样本和女性声音样本随机地分布到训练和测试数据集，这里使用随机算法随机选取2000条作为训练数据集，其余的1168条作为测试数据集：

# 随机划分数据集为训练集 和 测试集
test_set = list(range(len(new_data_set)))
train_set = []
for i in range(2000):
	random_index = int(np.random.uniform(0, len(test_set)))
    train_set.append(test_set[random_index])
    del test_set[random_index]

# 训练数据集
train_mat = []
train_classes = []
for index in train_set:
	train_mat.append(new_data_set[index])
    train_classes.append(list_class[index])

# 测试数据集
test_mat = []
test_classes = []
for index in test_set:
	test_mat.append(new_data_set[index])
    test_classes.append(list_class[index])

5.2 朴素贝叶斯分类器实现

        我们假设20个特征值分类为 $F1,F2,F3\cdots F20$，$F{1}_{i1}$ 表示 特征 $F1$ 取 第 $i1$ 个分类。

        则一个测试样本向量可以表示如下：
$$tes{t}_{v}ector=[F{1}_{i1},F{2}_{i2},F{3}_{i3}\cdots ,F19_{i19},F20_{i20}]$$

        则其是男性的概率为：

$$\begin{gathered} P(男|F{1}_{i1}\times F{2}_{i2}\times F{3}_{i3}\cdots F19_{i19}\times F20_{i20}) \\ =P(F{1}_{i1}\times F{2}_{i2}\times F{3}_{i3}\cdots F19_{i19}\times F20_{i20}|男)\ast P(男)/P(F{1}_{i1}\times F{2}_{i2}\times F{3}_{i3}\cdots F19_{i19}\times F20_{i20}) \end{gathered}$$

1. 代码实现

def native_bayes(train_matrix, list_classes):
    """
    :param train_matrix: 训练样本矩阵
    :param list_classes: 训练样本分类向量
    :return:p_1_class 任一样本分类为1的概率  p_feature,p_1_feature 分别为给定类别的情况下所以特征所有取值的概率
    """

    # 训练样本个数
    num_train_data = len(train_matrix)
    num_feature = len(train_matrix[0])
    # 分类为1的样本占比
    p_1_class = sum(list_classes) / float(num_train_data)

    n = 10
    list_classes_1 = []
    train_data_1 = []

    for i in list(range(num_train_data)):
        if list_classes[i] == 1:
            list_classes_1.append(i)
            train_data_1.append(train_matrix[i])

    # 分类为1 情况下的各特征的概率
    train_data_1 = np.matrix(train_data_1)
    p_1_feature = {}
    for i in list(range(num_feature)):
        feature_values = np.array(train_data_1[:, i]).flatten()
        # 避免某些特征值概率为0 影响总体概率，每个特征值最少个数为1
        feature_values = feature_values.tolist() + list(range(n))
        p = {}
        count = len(feature_values)
        for value in set(feature_values):
            p[value] = np.log(feature_values.count(value) / float(count))
        p_1_feature[i] = p

    # 所有分类下的各特征的概率
    p_feature = {}
    train_matrix = np.matrix(train_matrix)
    for i in list(range(num_feature)):
        feature_values = np.array(train_matrix[:, i]).flatten()
        feature_values = feature_values.tolist() + list(range(n))
        p = {}
        count = len(feature_values)
        for value in set(feature_values):
            p[value] = np.log(feature_values.count(value) / float(count))
        p_feature[i] = p

    return p_feature, p_1_feature, p_1_class

2. 问题分析

问题1：
        因为计算中有 $P(F{1}_{i1}\times F{2}_{i2}\times F{3}_{i3}\cdots F19_{i19}\times F20_{i20})=P(F{1}_{i1})\ast P(F{2}_{i2})\cdots P(F20_{i20})$

        需要多个概率相乘，但如果某个概率为0，则总的概率就会为0，这样计算就会出现错误，所以这里给每个分类至少添加一条数据，如上图第29行和第41行。

问题2：
        因为本文的数据集有20个特征，多个特征的概率相乘，乘积的结果将会非常小，可能会在四舍五入过程中被舍弃掉，从而影响实验结果。所以这里统一取对数，如上图第33行和45行。

5.3 测试分类效果

        按照贝叶斯公式，计算测试样本在特定条件下 为男性的概率 和 为女性的概率，选取概率大的分类为最终的分类：

def classify_bayes(test_vector, p_feature, p_1_feature, p_1_class):
    """
    :param test_vector: 要分类的测试向量
    :param p_feature: 所有分类的情况下特征所有取值的概率
    :param p_1_feature: 类别为1的情况下所有特征所有取值的概率
    :param p_1_class: 任一样本分类为1的概率
    :return: 1 表示男性 0 表示女性
    """
    # 计算每个分类的概率(概率相乘取对数 = 概率各自对数相加)
    sum = 0.0
    for i in list(range(len(test_vector))):
        sum += p_1_feature[i][test_vector[i]]
        sum -= p_feature[i][test_vector[i]]
    p1 = sum + np.log(p_1_class)
    p0 = 1 - p1
    if p1 > p0:
        return 1
    else:
        return 0

测试代码：

def test_bayes():
    file_name = 'data/voice.csv'
    train_mat, train_classes, test_mat, test_classes, label_name = load_data_set(file_name)

    p_feature, p_1_feature, p_1_class = native_bayes(train_mat, train_classes)

    count = 0.0
    correct_count = 0.0

    for i in list(range(len(test_mat))):
        test_vector = test_mat[i]
        result = classify_bayes(test_vector, p_feature, p_1_feature, p_1_class)
        if result == test_classes[i]:
            correct_count += 1
        count += 1
    print(correct_count / count)


test_bayes()

        朴素贝叶斯分类器的原理和实现都比较简单，这是基于各个特征都是相对独立的情况，算法里也没有复杂的求导和矩阵运算，因此效率很高。为了提高识别率，还可以通过比如特征加权、增加特征值离散程度等改进办法来实现。

更多案例分析，请阅读：Kaggle比赛之“旧金山犯罪分类预测”、怎样写一个拼写检查器、朴素贝叶斯算法示例：文本数据分类

---

6 小结

6.1 优缺点分析

优点：

1. 对小规模的数据表现很好，适合多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练；

2. 对缺失数据不太敏感，算法也比较简单，常用于文本分类；

3. 发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率，当数据呈现不同的特点时，分类性能不会有太大的差异，健壮性好；

4. 当数据集属性之间的关系相对比较独立时，朴素贝叶斯分类算法会有较好的效果。

缺点：

1. 对输入数据的表达形式很敏感（离散、连续，值极大极小之类的）；

2. 需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳；

3. 由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率；

4. 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

6.2 内容拓展

1. 半朴素贝叶斯分类器：在朴素的分类中， 我们假定了各个属性之间的独立，这是为了计算方便，防止过多的属性之间的依赖导致的大量计算。这正是朴素的含义，虽然朴素贝叶斯的分类效果不错，但是属性之间毕竟是有关联的， 某个属性依赖于另外的属性， 于是就有了半朴素贝叶斯分类器。

2. 朴素贝叶斯与LR的区别？简单来说：朴素贝叶斯是生成模型，根据已有样本进行贝叶斯估计学习出先验概率 $P(Y)$ 和条件概率 $P(X|Y)$，进而求出联合分布概率 $P(XY)$，最后利用贝叶斯定理求解 $P(Y|X)$， 而LR是判别模型，根据极大化对数似然函数直接求出条件概率 $P(Y|X)$；朴素贝叶斯是基于很强的条件独立假设（在已知分类 $Y$ 的条件下，各个特征变量取值是相互独立的），而LR则对此没有要求；朴素贝叶斯适用于数据集少的情景，而LR适用于大规模数据集。

3. 在估计条件概率 $P(X|Y)$ 时出现概率为0的情况怎么办？简单来说：引入 $\lambda$，当 $\lambda =1$ 时称为拉普拉斯平滑。

4. 一句话概况朴素贝斯：是一个生成模型（很重要），其次它通过学习已知样本，计算出联合概率，再求条件概率。

5. 生成模式和判别模式的区别：生成模式：由数据学得联合概率分布，求出条件概率分布 $P(Y|X)$ 的预测模型；常见的生成模型有：朴素贝叶斯、隐马尔可夫模型、高斯混合模型、文档主题生成模型（LDA）、限制玻尔兹曼机。判别模式：由数据学得决策函数或条件概率分布作为预测模型；常见的判别模型有：K近邻、SVM、决策树、感知机、线性判别分析（LDA）、线性回归、传统的神经网络、逻辑斯蒂回归、boosting、条件随机场。

思维导图：

---

参考

• 算法杂货铺——分类算法之朴素贝叶斯分类(Naive Bayesian classification)：https://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html
• 机器学习之朴素贝叶斯详解：https://www.cnblogs.com/bonheur/p/12469873.html
• 朴素贝叶斯算法原理小结：https://www.cnblogs.com/pinard/p/6069267.html
• 朴素贝叶斯以及三种常见模型推导：https://www.jianshu.com/p/b6cadf53b8b8
• 机器学习–用朴素贝叶斯分类法辨别男女声音：https://www.cnblogs.com/beiyan/p/8337991.html