IOU GIOU DIOU CIOU 及代码实现

总体发展过程：

IOU 

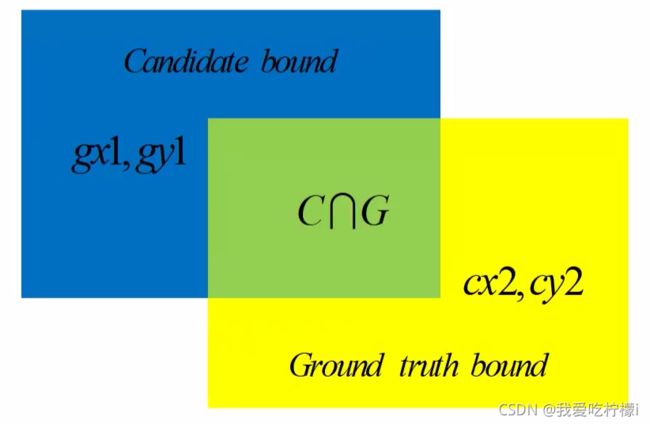
IOU(交并比)顾名思义就是两个框的交集除以他们的并集。

IOU Loss：IOU Loss = 1 －IOU(比较常用) 

IOU 的优点：1.能够很好的反应重合的程度       2.具有尺度不变性

缺点： 当不相交时候loss为0 （IOU Loss = 1 - IOU）

GIOU 

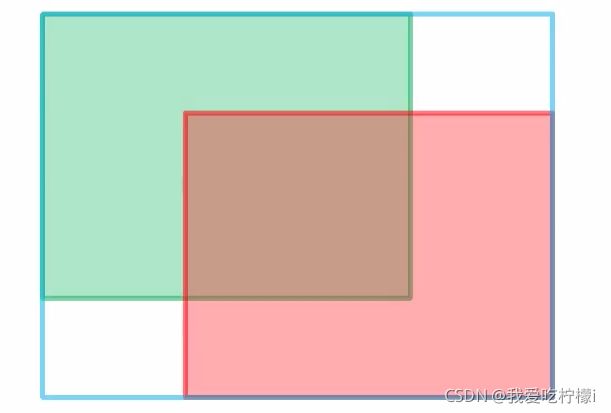
        如图绿色边界框为真实的边界框，红色边界框为网络预测的边界框，蓝色边界框为用最小的矩形把两个边界框给框住。 = 蓝色目标边界框面积。u=两个边界框并集的面积。取两个极限的例子，当两个目标边界框重合时，- u = 0。此时GIOU = IOU。此时IOU = 1。当两个边界框无穷远时趋近于1 ，GIOU = IOU - 1，此时IOU = 0，所以此时的GIOU = -1。GIOU的范围在-1到1之间。对比IOU当两个目标框不相交时也能提供损失。

GIOU Loss：1 - GIOU

特殊情况下GIOU会变为IOU：

DIOU:

        IOU和GIOU有两个很大的缺点：1.收敛特别慢   2.回归的不够准确。为此作者提出了DIOU

         DIOU能够更好地反映两个框的相交情况，将其用于计算网络的损失函数可以直接最小化两框之间的距离，收敛速度更快。

        其中代表两者之间的欧氏距离。为黑色框代表预测的边界框，为绿色框代表真实框。。为两个边界框最小外界框的对角线的长度。同GIOU的计算方法，可以算出DIOU 的取值范围。

DIOU 损失能够直接最小化两个boxes之间的距离，因此收敛的速度更快。

DIOU Loss： 1 - DIOU

CIOU：

        作者认为对于一个优秀的回归定位损失应该考虑到3种几何参数：重叠面积  中心点距离  长宽比。因此作者在DIOU的基础上加上了长宽比。

CIOU Loss = 1 - CIOU 

CIOU(D) : 将CIOU中的IOU换成DIOU

代码:

class IOUloss(nn.Module):
    def __init__(self, reduction="none", loss_type="diou"):
        super(IOUloss, self).__init__()
        self.reduction = reduction
        self.loss_type = loss_type

    def forward(self, pred, target):
        assert pred.shape[0] == target.shape[0]
        pred = pred.view(-1, 4)
        target = target.view(-1, 4)

        tl = torch.max(
            (pred[:, :2] - pred[:, 2:] / 2), (target[:, :2] - target[:, 2:] / 2)
        )
        br = torch.min(
            (pred[:, :2] + pred[:, 2:] / 2), (target[:, :2] + target[:, 2:] / 2)
        )

        area_p = torch.prod(pred[:, 2:], 1)
        area_g = torch.prod(target[:, 2:], 1)

        en = (tl < br).type(tl.type()).prod(dim=1)
        area_i = torch.prod(br - tl, 1) * en
        area_u = area_p + area_g - area_i
        iou = (area_i) / (area_u + 1e-16)


        #########################################siou#########################################
        # ----------------------------------------------------#
        #   计算中心的差距
        # ----------------------------------------------------#
        center_wh = (pred[:, :2] - target[:, :2])  # 中心距离

        # ----------------------------------------------------#
        #   找到包裹两个框的最小框的左上角和右下角
        # ----------------------------------------------------#
        b1_wh = pred[:, 2:]
        b2_wh = target[:, 2:]
        # b1_mins = pred[:, :2] - (pred[:, 2:] / 2)      # 预测框的左上角
        # b2_mins = target[:, :2] - (target[:, 2:] / 2)   # 真实框的左上角
        # b1_maxes = pred[:, :2] + (pred[:, 2:] / 2)    # 预测框的左上角
        # b2_maxes = target[:, :2] + (target[:, 2:] / 2)  # 真实框的右下角
        # intersect_maxes = torch.min(b1_maxes, b2_maxes)  # 交集右下角坐标
        intersect_maxes = torch.min(
            (pred[:, :2] + pred[:, 2:] / 2), (target[:, :2] + target[:, 2:] / 2)  # 两框右下角最大点（x为基准）
        )
        # enclose_mins = torch.min(b1_mins, b2_mins)
        # enclose_maxes = torch.max(b1_maxes, b2_maxes)

        enclose_mins = torch.min(
                (pred[:, :2] - pred[:, 2:] / 2), (target[:, :2] - target[:, 2:] / 2)   # 两框左上角最小点（x为基准）
            )
        enclose_maxes = torch.max(
                (pred[:, :2] + pred[:, 2:] / 2), (target[:, :2] + target[:, 2:] / 2)   # 两框右下角最大点（x为基准）
            )
        enclose_wh = torch.max(enclose_maxes - enclose_mins, torch.zeros_like(intersect_maxes))  # torch.zeros_like：产生一个与a相同shape的Tensor.
        #########################################siou#########################################


        if self.loss_type == "iou":
            loss = 1 - iou ** 2
            print('loss = ', loss)

        elif self.loss_type == "diou":  # xywh

            # ----------------------------------------------------#
            #   计算中心的距离
            # ----------------------------------------------------#
            center_distance = torch.sum(torch.pow(center_wh, 2), axis=-1)  # x平方+y平方  ρ方（b，bgt）

            # ----------------------------------------------------#
            #   计算对角线距离
            # ----------------------------------------------------#
            enclose_diagonal = torch.sum(torch.pow(enclose_wh, 2), axis=-1)  # x平方+y平方

            diou = iou - 1.0 * (center_distance) / torch.clamp(enclose_diagonal, min=1e-6)  # torch.clamp：限制最小值为1e-6


            loss = 1 - diou



        elif self.loss_type == "giou":    # xywh
            c_tl = torch.min(
                (pred[:, :2] - pred[:, 2:] / 2), (target[:, :2] - target[:, 2:] / 2)   # 两框左上角最小点（x为基准）
            )
            c_br = torch.max(
                (pred[:, :2] + pred[:, 2:] / 2), (target[:, :2] + target[:, 2:] / 2)   # 两框右下角最大点（x为基准）
            )

            area_c = torch.prod(c_br - c_tl, 1)   # torch.prod：在1维度上，返回 input 张量中所有元素的乘积。
            giou = iou - (area_c - area_u) / area_c.clamp(1e-16)
            loss = 1 - giou.clamp(min=-1.0, max=1.0)   # clamp：限制在-1到1中间
            print('loss = ', loss)
        elif self.loss_type == "ciou":  # xywh
            # ----------------------------------------------------#
            #   计算中心的距离
            # ----------------------------------------------------#
            center_distance = torch.sum(torch.pow(center_wh, 2), axis=-1)  # x平方+y平方  ρ方（b，bgt）


            # ----------------------------------------------------#
            #   计算对角线距离
            # ----------------------------------------------------#
            enclose_diagonal = torch.sum(torch.pow(enclose_wh, 2), axis=-1)  # x平方+y平方

            ciou = iou - 1.0 * (center_distance) / torch.clamp(enclose_diagonal, min=1e-6)  # torch.clamp：限制最小值为1e-6

            # v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(
            #     pred[:, 2] / torch.clamp(pred[:, 3], min=1e-6)) - torch.atan(target[:, 2] / torch.clamp(target[:, 3], min=1e-6))), 2)   # torch.atan：包含输入input张量每个元素的反正切函数。
            v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(
                b1_wh[..., 0] / torch.clamp(b1_wh[..., 1], min=1e-6)) - torch.atan(
                b2_wh[..., 0] / torch.clamp(b2_wh[..., 1], min=1e-6))), 2)
            alpha = v / torch.clamp((1.0 - iou + v), min=1e-6)
            out = ciou - alpha * v
            loss = 1 - out

        elif self.loss_type == 'siou':
            # ----------------------------------------------------#
            #   Angle cost
            # ----------------------------------------------------#
            # ----------------------------------------------------#
            #   计算中心的距离
            # ----------------------------------------------------#
            sigma = torch.pow(torch.sum(torch.pow(center_wh, 2), axis=-1), 0.5)
            # ----------------------------------------------------#
            #   求h和w方向上的sin比值
            # ----------------------------------------------------#
            sin_alpha_1 = torch.clamp(torch.abs(center_wh[:, 0]) / torch.clamp(sigma, min=1e-6), min=0, max=1)
            sin_alpha_2 = torch.clamp(torch.abs(center_wh[:, 1]) / torch.clamp(sigma, min=1e-6), min=0, max=1)
            # ----------------------------------------------------#
            #   求门限，二分之根号二，0.707
            #   如果门限大于0.707，代表某个方向的角度大于45°
            #   此时取另一个方向的角度
            # ----------------------------------------------------#
            threshold = pow(2, 0.5) / 2
            sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)
            # ----------------------------------------------------#
            #   alpha越接近于45°，angle_cost越接近于1，gamma越接近于1
            #   alpha越接近于0°，angle_cost越接近于0，gamma越接近于2
            # ----------------------------------------------------#
            angle_cost = torch.cos(torch.asin(sin_alpha) * 2 - math.pi / 2)
            gamma = 2 - angle_cost
            # ----------------------------------------------------#
            #   Distance cost
            #   求中心与外包围举行高宽的比值
            # ----------------------------------------------------#
            rho_x = (center_wh[:, 0] / torch.clamp(enclose_wh[:, 0], min=1e-6)) ** 2
            rho_y = (center_wh[:, 1] / torch.clamp(enclose_wh[:, 1], min=1e-6)) ** 2
            distance_cost = 2 - torch.exp(-gamma * rho_x) - torch.exp(-gamma * rho_y)
            # ----------------------------------------------------#
            #   Shape cost
            #   真实框与预测框的宽高差异与最大值的比值
            #   差异越小，costshape_cost越小
            # ----------------------------------------------------#
            omiga_w = torch.abs(b1_wh[:, 0] - b2_wh[:, 0]) / torch.clamp(torch.max(b1_wh[:, 0], b2_wh[:, 0]),
                                                                             min=1e-6)
            omiga_h = torch.abs(b1_wh[:, 1] - b2_wh[:, 1]) / torch.clamp(torch.max(b1_wh[:, 1], b2_wh[:, 1]),
                                                                             min=1e-6)
            shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)
            out = iou - 0.5 * (distance_cost + shape_cost)
            loss = 1 - out



        if self.reduction == "mean":
            loss = loss.mean()
        elif self.reduction == "sum":
            loss = loss.sum()

        return loss