随机森林（Random Forest）学习笔记
0 声明
本文主要内容来自视频 '【2020机器学习全集】菜菜的sklearn完整版，价值4999元的最全机器学习sklearn全集，赶紧收藏_哔哩哔哩_bilibili' 以及视频课件“https://pan.baidu.com/s/1Xl4o0PMA5ysUILeCKvm_2w，提取码：a967”。
本文是一个学习笔记，不是一篇帮助新人入门的文章，其内容主要针对本人的薄弱环节，没有面面俱到，不一定适用所有人。
本文主要介绍了集成算法的概念、使用sklearn实现随机森林的重要参数、属性以及方法、调参的基本思路等。
最后，阅读本文需要有使用sklearn实现决策树的基础知识。
1 集成算法
如果说修长城靠的是人多力量大的话，那么集成算法就堪称树多力量大的典范——该算法使用了多个子树（子模型）对给定数据集执行分析操作。如果集成算法中各个模型相互独立，互不影响，那么该集成算法叫做Bagging方法，否则叫做Boosting方法。
Bagging方法通过构建多个相互独立的评估器对给定数据进行评估操作，然后输出各自的分析结果，按照少数服从多数或者取平均的原则决定最终的输出结果。本文要讲解的随机森林就是Bagging方法的典型代表。此外，Boosting方法也是十分重要的集成方法，但鉴于不是本文的探讨范围，不再赘述。
2 随机森林抽样方法——有放回的随机抽样
之所以要对训练样本N进行随机抽样，是为了保证随机森林各个子模型的训练集基本不同，以达到各个子模型相互独立的要求。维持子模型训练样本基本不同之所以很重要，是因为若每个子模型的训练集均一致，那么随机森林最终得到的决策结果也将完全一样，随机森林算法就完全等价于单个决策树算法，完全没有体现使用集成算法的优势。
随机抽样分为两种，一种是无放回的随机抽样，另一种是有放回的随机抽样，随机森林使用的是后者。稍作思考便会发现，若要保证各子模型相互独立，似乎使用无放回的随机抽样更好——对于n个子模型的随机森林而言，将N个训练集平均分成n份，再将其分给各个子模型用作训练的采样方法似乎才能保证随机森林的完全相互独立。事实上，采用随机森林算法的目的不是为了得到几个独立的子模型，而是要根据各个子模型输出的结果来进行联合判定。如果几个子模型所用的样本完全不同，那似乎就相当于找了几个“毫无关系”的决策树，强行组成随机森林，这种随机森林的团队协作效率估计不会太好。基于以上原因，随机森林选择的是有放回的随机抽样。
3 Out-of-bag Data
有放回地随机抽样方法的特点决定了每个子模型的训练集中可能会存在重复的样本。对一个数量为n的测试集，有放回地抽样n次得到数量为n的子树的测试集合（是的，每个子树测试集的数量等于原始测试集的数量），每一个样本被抽到数据集的概率使用以下公式计算（使用高中数学独立重复实验的公式，采用间接法可以很快得出）：
当n足够大时，利用高等数学的重要极限公式，可以得到得到上式收敛于
。也就是说对于每一颗子树而言，当样本数足够大时，每个元素被选到的概率为0.632，剩下0.368的数据没有被选中作为训练集，这部分没有被选中作为训练集的数据称之为Out-of-bag Data（袋外数据）。
利用随机森林使用有放回随机抽样的这种特性，当n足够大时，可以不必划分测试集与训练集，直接使用Out-of-bag Data进行测试即可。
4 使用sklearn实现随机森林分类器
4.1 重要参数
4.1.1 子树的参数
子树的参数可以参考'决策树算法学习笔记_liuqihang11的博客-CSDN博客'，这里不再赘述。
4.1.2 n_estimators
n_estimators表示子树的数量，当n_estimators较小时，随着n_estimators越大，模型的效果往往越好；当n_estimators达到一定的程度之后，随机森林的精确性往往开始波动，并且，n_estimators越大，需要的计算量和内存也越大，训练的时间也会越来越长。从sklearn的0.22版本开始，n_estimators默认为100。
4.1.3 random_state
原始数据集存在多个特征，决策树从最优的特征中随机取出一个特征进行分支，这就造成了每次生成的决策树都不一样。为了获取可重复的试验结果，使用random_state参数进行控制，命令决策树每次都选择相同的特征作为根节点。
以上是决策数中random_state的用法，而在随机森林中，random_state的用法有所不同。决策树中的random_state控制一棵树的生长行为，而随机森林的random_state直接着眼于整个森林的生长，它不要求（也不应该要求）每颗树长得一致。每次使用random_state都会生成同一片森林，这片森林还是由原来那些相互不同的数组成的。
补充，或许有人会觉得既然是最优的特征，当然就应该只有一个，怎么会有“从最优的特征中随机取出一个特征”这种说法呢？我认为原因在于：对于一组特征来说，当然只有一个最重要的特征，这个最重要的的特征一定是客观存在的，但是要将他找出来需要花费的计算代价过高，故采取了一种基于贪心算法的妥协方式来寻找最优的特征，该方法并不在全局中寻找，而是获取各个局部的最优特征，然后将这些最优特征组成一个集合，再从这里面随机选择一个作为根节点。
4.1.4 bootstrap与oob_score参数
bootstrap参数默认True，代表有放回随机抽样，该参数一般不会去改动。
oob_score参数设置为true表示使用Out-of-bag Data进行测试。
4.2 重要属性与方法
| .estimators_ | 以列表形式输出包含单个决策树信息 |
| .feature_importances | 返回每个特征的重要性，一般是这个特征在多次分枝中产生的信息增益的综合，也被称为“基尼重要性”(Gini lmportance) |
| .oob_score_ | 输出浮点数，使用袋外数据来验证模型效益的分数 |
| .predict(X) | 输入测试集X，返回测试集的预测结果Y |
| .fit(X,Y) | 使用训练集X与Y进行训练 |
| .score(X,Y) | 使用测试集X与Y测试模型准确度 |
| .predict_proba接口 |
返回每个测试样本对应的被分到每一类标签的概率，标签有几个分类就返回几个概率。如果是二分类问题，则predict_proba返回的数值大于0.5的，被分为1，小于0.5的，被分为0。sklearn中的随机森林是平均每个样本对应的predict_proba返回的概率，得到一个平均概率，从而决定测试样本的分类 |
4.3 一个随机森林分类器实例
from sklearn.datasets import load_wine
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split # 划分训练集和测试集
wine = load_wine() # 导入红酒数据集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data, wine.target, test_size=0.3)
# 0.3做测试集，顺序别乱
rfc = RandomForestClassifier(random_state=1) # 随机森林分类
rfc = rfc.fit(Xtrain, Ytrain)
score_r = rfc.score(Xtest, Ytest) # 计算准确度5 使用sklearn实现随机森林回归器
5.1 重要参数
5.1.1 控制子树的参数
控制子树的参数同决策回归树的参数完全一致，可参考'决策树算法学习笔记_liuqihang11的博客-CSDN博客'，这里不再赘述。
5.1.2 其他
其他的重要参数、属性与接口与随机森林分类器一致，但是需要指出的是随机森林回归器没有有predict_proba方法。
5.2 随机森林回归器实例
from sklearn.datasets import load_boston # 一个标签是连续变量的数据集
from sklearn.model_selection import cross_val_score # 导入交叉验证模块
from sklearn.ensemble import RandomForestRegressor # 导入随机森林回归器
# 随机森林回归器的scoring默认返回R2
boston = load_boston()
regressor = RandomForestRegressor(n_estimators=100, random_state=0) # 实例化
cross_val_score(regressor, boston.data, boston.target, cv=10, scoring="neg_mean_squared_error" # 如果不写scoring，回归评估默认是R平方
6 随机森林调参思路
6.1 泛化误差
泛化误差是一个衡量模型迁移能力的指标，使用训练数据训练出来的模型在OBB数据或者测试数据上的表现可以用泛化误差来体现，泛化误差低，模型迁移能力好，否则不好。 一个集成模型f在未知数据集(D)上的泛化误差E(f;D)可以使用方差var、偏差bias与噪声
来衡量：
所谓的偏差，是指模型的预测值与真实值之间的差异。在集成算法中，每个子树都会有自己的偏差，集成评估器的偏差是所有基评估器偏差的均值。模型越精确，偏差越低。
所谓的方差，是指模型每一次输出结果与模型预测值的平均水平之间的误差。衡量模型的稳定性。模型越稳定，方差越低。
所谓的噪声，是指一些不稳定的因素，这些因素不在人的影响范围内，因此不谈。
| 偏差大 | 偏差小 | |
| 方差大 | 模型不适合这个数据 更换模型 |
过拟合 模型复杂 对某些数据预测很准 对某些数据预测很差 |
| 方差小 | 欠拟合 模型相对简单 预测很稳定 预测不准 |
总的的泛化误差小，调参的目标 |
方差和偏差有一个很大，泛化误差都会很大。然而，方差和偏差是此消彼长的，不可能同时达到最小。下图给出了泛化误差与模型复杂度、模型复杂度与方差和偏差的关系曲线。从图中可以看出，模型越复杂，方差越大，偏差越小，总的泛化误差越高；模型越简单，偏差越大，方差越小，总的泛化误差越大。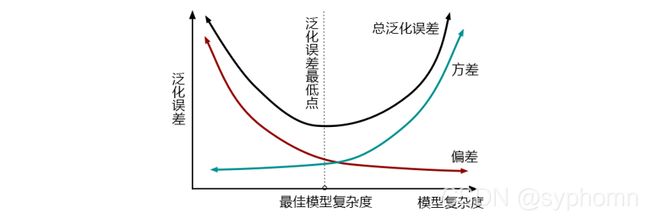
对于随机森林而言，max_depth, min_samples, min_samples_leaf等参数都是默认设置为最高复杂度的值，因此其模型天生位于上图的右上角，那么调参方向就应该是降低模型复杂度的方向，总结而言就是下面4句话：
（1）模型太复杂或者太简单，都会让泛化误差高，我们追求的是位于中间的平衡点
（2）模型太复杂就会过拟合，模型太简单就会欠拟合
（3）对树模型和树的集成模型来说，树的深度越深，枝叶越多，模型越复杂
（4）树模型和树的集成模型的目标，都是减少模型复杂度，把模型往图像的左边移动
6.2 调参步骤
（1）调节n_estimators，默认数值为100，调参目标是使得准确率曲线提升至平稳，该参数不影响单个模型的复杂度；
（2）max_depth：默认是最大深度，即最高复杂度，max_depth减小，模型更简单，泛化偏差往图像左边移动，对于小型数据，可以取1-20，大型数据可以考虑30-50；
（3）min_samples_leaf：默认为1，即最高复杂度，增大max_samples_leaf，模型更简单，泛化误差且向图像的左边移动，每次可以增加10-20，高维数据可以一次增加50试试；
（4）min_samples_split：默认最小限制2，即最高复杂度，增大min_samples_splitt，模型更简单，泛化误差向图像的左边移动，每次可以增加10-20，高维数据可以一次增加50试试；
（5）max_features：默认是特征总数开平方，既可以向复杂度升高的方向，也可以向复杂度降低的方向调参；
（6）criterion：entropy与gini两种都可以试试。
（7）class_weight：当标签分布不均衡时，设置将其设置为"balanced"以均衡标签。
7 补充问题
7.1 为什么随机森林算法能够提高准确率
假设一个随机森林有n颗树，每颗树的准确率为Pi（i =1,2,...,n），如果按照少数服从多数的原则来决定最终结果的话，那至少需要一半以上的子树出现错误才会导致错误结果的输出，出错的概率计算公式如下：
![{{P}_{wrong}}=C_{n}^{[\frac{n}{2}]+1}\prod\limits_{i=1}^{i=[\frac{n}{2}]+1}{{{(1-P}_{i})}}](http://img.e-com-net.com/image/info8/9517757b8a794f12ab78356f09fc76e1.gif)
其中，[ ]表示向下取整函数，若本身就是整数则原地输出，Pi为每颗树的正确率，n为树的数量，Pwrong为出错的概率。
为什么随机森林算法能够提高准确率呢？其实就是需要判断下式是否恒成立：
![{{P}_{wrong}}=C_{n}^{[\frac{n}{2}]+1}\prod\limits_{i=1}^{i=[\frac{n}{2}]+1}{(1-{{P}_{i}})<\underset{n}{\mathop{min}}\,({{1-P}_{j}})}](http://img.e-com-net.com/image/info8/25d2de5fe56a43658994b664964736ec.gif)
（*）
从上面的表达式可以看出，左边的值是与树的数量n、每棵树的准确率Pi有关的；而右边表示的是这n颗树中准确率的最小值。如果能够证明上式恒成立，那就可以说随机森林与单颗决策树相比一定能够提高准确率。
显然，上式不是恒成立的。不妨试想一种极端情况，随机森林有两棵树，一颗准确率为1，另一颗准确率为0，显然上式的不成立的。到这里，便可以说：随机森林是不一定能够提高准确率的。基于以上讨论，又衍生出了下面的第二个问题。
7.2 随机森林一定能够提高准确率的条件是什么
一般认为要使得（*）成立的条件是每个子树的准确率不得低于50%。事实上，这个结论成立的前提是每颗子树的准确率均相同，但这其实是不准确的，因为在所有随机森林中，每棵树的准确率基本都不是相同的。然而准确率在不同条件下的理论推导难度属实太大，就只好假设每颗树的准确率均相等，基于这个假设推导出来的子树准确率必须要保证在50%以上。实际操作中，即使存在个别子树的准确率低于百分之五十，随机森林的准确率也有可能优于单颗子树。
但总的来说，我认为还是应该尽力保证单颗子树准确率高于50%这一基本要求，毕竟50%的准确率本身就不高，要是有子树低于这个数，考虑的可能就不是随机森林是否优于单颗决策树的问题，而是随机森林是不是适用这个数据集的问题了。
.