图像处理与小波变换-Python实现

关于小波变换的理论知识，可以查看我的另一篇文章→小波变换入门

本文主要介绍小波变换在图像分解中的应用及其Python实现。

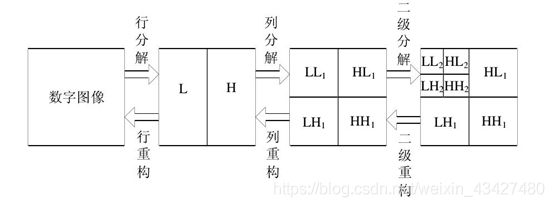
      按照滤波组理论，图像的二维离散小波分解和重构过程如下图所示，分解过程可描述为：首先对图像的每一行进行 1D-DWT，获得原始图像在水平方向上的低频分量 L 和高频分量 H，然后对变换所得数据的每一列进行 1D-DWT，获得原始图像在水平和垂直方向上的低频分量 LL、水平方向上的低频和垂直方向上的高频 LH、水平方向上的高频和垂直方向上的低频 HL 以及水平和垂直方向上的的高频分量 HH。

      重构过程可描述为：首先对变换结果的每一列进行一维离散小波逆变换，再对变换所得数据的每一行进行一维离散小波逆变换，即可获得重构图像。由上述过程可以看出，图像的小波分解是一个将信号按照低频和有向高频进行分离的过程，分解过程中还可以根据需要对得到的 LL 分量进行进一步的小波分解，直至达到要求。

import cv2.cv2 as cv
import numpy as np
from pywt import dwt2, wavedec2
import matplotlib.pyplot as plt

im = cv.imread('f:/image/cat.jpg', 0)
if im.shape[1] > 500:
    (h, w) = im.shape[:2]
    width = 500
    height = int(h * (width / float(w)))
    im = cv.resize(im, (width, height), interpolation=cv.INTER_AREA)

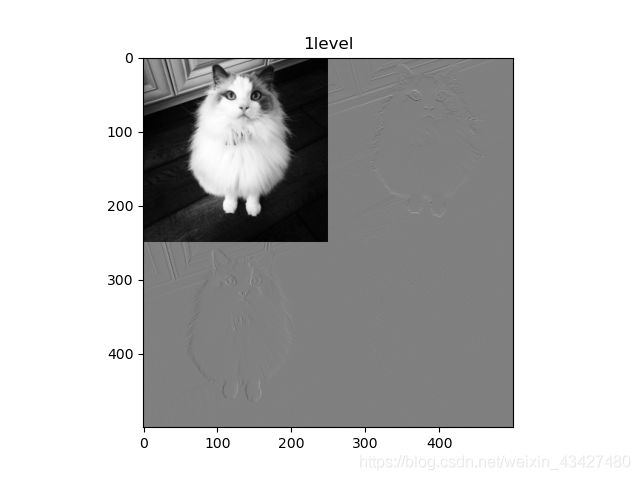
#单级小波分解，返回分别为低频分量，水平高频，竖直高频，对角高频，分别相当于上图中LL,HL,LH,HH
cA, (cH, cV, cD) = dwt2(im, 'haar')
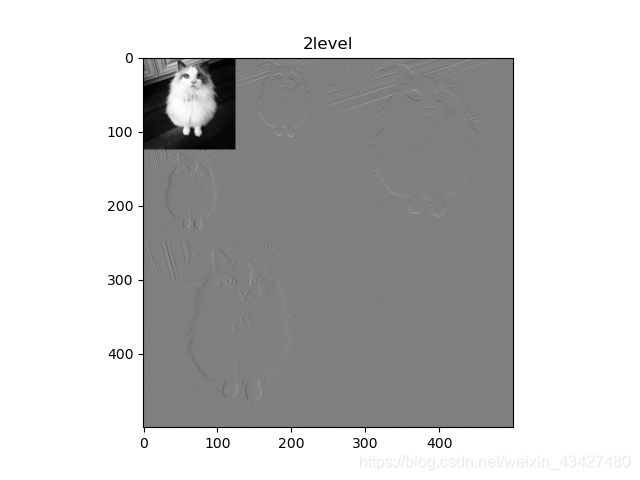
#二级小波分解
cA2, (cH2, cV2, cD2), (cH1, cV1, cD1) = wavedec2(im, 'haar', level=2)

#将各个子图拼接(低频cA取值范围[0,510],高频[-255,255])
AH = np.concatenate([cA, cH+255], axis=1)  #axis=1表示列拼接
VD = np.concatenate([cV+255, cD+255], axis=1)
res1 = np.concatenate([AH, VD], axis=0)

AH2 = np.concatenate([cA2, cH2+510], axis=1)
VD2 = np.concatenate([cV2+510, cD2+510], axis=1)
A2 = np.concatenate([AH2, VD2], axis=0)
AH1 = np.concatenate([A2, (cH1+255)*2], axis=1)
VD1 = np.concatenate([(cV1+255)*2, (cD1+255)*2], axis=1)
res2 = np.concatenate([AH1, VD1], axis=0)

#显示
plt.figure('2D_DWT_1level')
plt.imshow(res1, cmap='gray', vmin=0, vmax=510)
plt.title('1level')

plt.figure('2D_DWT_2level')
plt.imshow(res2, cmap='gray', vmin=0, vmax=1020)
plt.title('2level')

plt.show()

原图：

一级分解：

二级分解：