卷积神经网络(CNN)与TensorFlow实现

CNN的简介

卷积神经网络（CNN）由输入层、卷积层、激活函数、池化层、全连接层组成，即INPUT-CONV-RELU-POOL-FC。CNN在图像识别、文本分类等方面都有着广泛的应用。本文将结合TensorFlow代码介绍一个完整的卷积神经网络中需要用到的以下内容：

• 输入层

*   reshape操作 

• 卷积层

*   填充(padding)
*   卷积(tf.nn.conv2d)
*   激活函数(relu)
*   池化(pooling)

• 全连接层

*   矩阵相乘(tf.matmul)
*   dropout

• 输出层

*   softmax

在文章的最后给出了TensorFlow实现两层卷积神经网络的完整示例代码。

网络结构和处理流程

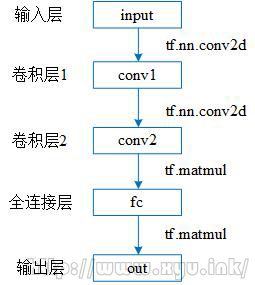
一个两层的卷积神经网络如下图所示：

上图可以进一步展开成如下图的形式：

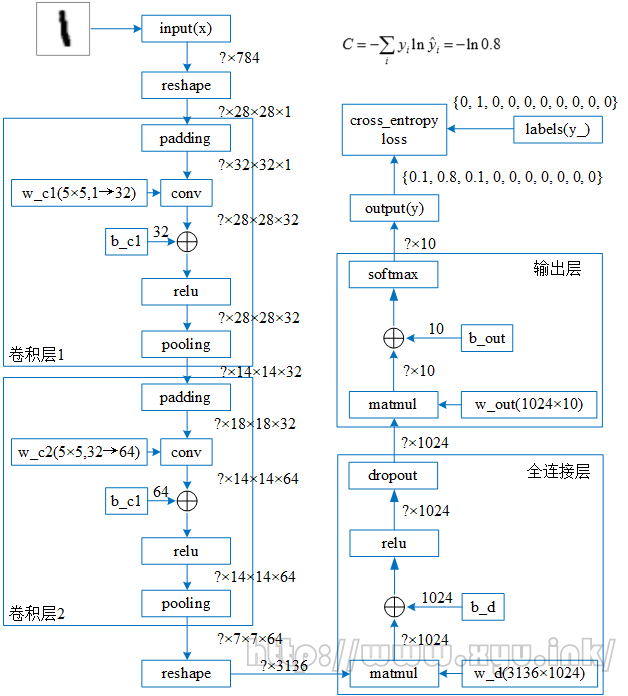
一个两层卷积神经网络的处理流程可以用文字描述为

• 输入

*   reshape操作(变为2维) 

• 卷积层1

*   填充(padding)
*   卷积(tf.nn.conv2d)
*   加上偏移b_c1
*   激活函数(relu)
*   池化(tf.nn.max_pool)

• 卷积层2(同卷积层1)
• 全连接层

*   reshape操作(变为1维) 
*   乘以权重w_d(tf.matmul)
*   加上偏移b_d
*   激活函数(relu)
*   dropout

• 输出层

*   乘以权重w_out(tf.matmul)
*   加上偏移b_out
*   激活函数(softmax)

下面以使用CNN对MNIST分类为例，分别对CNN中的每个处理操作加以介绍。
　　MNIST数据集介绍

约定符号：

• 输入图像： $$n\times n$$
• filter(过滤器)： $$f\times f$$
• padding(填充)： $$p$$
• stride(步长)： $$s$$
  本文中使用的 $$n=28,f=5,s=1,p=\frac{f-1}{2}=2$$

1.reshape

x = tf.placeholder(tf.float32, [None, 784])
x_reshape = tf.reshape(x, [-1, 28, 28, 1])

由于使用的是CNN对图像进行分类，所以不能再(像MLP一样)使用784维的向量表示输入x，而是要将其还原成28×28的图片形式。[-1, 28, 28, 1]中的-1表示第一维大小是由x自动确定的(因为x表示一个batch,而一个batch可以有若干副图片)。最后一个1表示通道数为1(因为MNIST数据集是灰度图片)。

2.padding

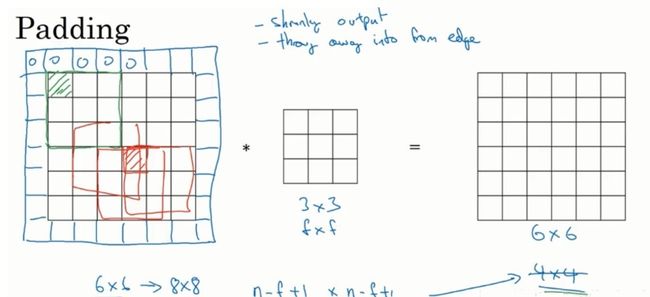
　　如果不先进行padding，直接使用5×5的过滤器对28×28的图像进行卷积操作，会得到24×24的图像(计算方法为n-f+1)。
　　但是这样会有两个缺点：
　　1. 图像会越来越小，无法保持原来的尺寸
　　2. 如上图所示，图像边缘的区域只会被一个过滤器经过，而中间的区域会被多个过滤器经过，这意味着边缘信息的丢失。

padding的两种模式

1.padding=‘VALID’
　　此时p=0，即不进行填充。
2.padding=‘SAME’
　　在图像的边缘填充"0"，每条边填充的大小为:

$$p=\displaystyle\frac{f-1}{2}=2 $$ 　　这样可以使得卷积操作后输出的图像尺寸保持不变(如详细结构图所示)

3.conv(卷积)

w_c1 = tf.Variable(tf.truncated_normal([5, 5, 1, 32], stddev=0.1), name='w_c1')
b_c1 = tf.Variable(tf.constant(0.1, shape=[32]), name='b_c1')
conv1 = tf.nn.conv2d(x_reshape, w_c1, strides=[1, 1, 1, 1], padding='SAME', name='conv1')
"""
tf.nn.conv2d(
    input,
    filter,
    strides,
    padding
)
    Args:
        input:  输入的张量
        filter: 过滤器,为变量Tensor(参数需要训练),形状为[filter_高, filter_宽, 输入通道数, 输出通道数]
        strides: 过滤器移动的步长
        padding: 填充算法,有两种方式,分别为"SAME"和"VALID"

"""

卷积的过程如下图所示(图转自参考资料[2])
　　
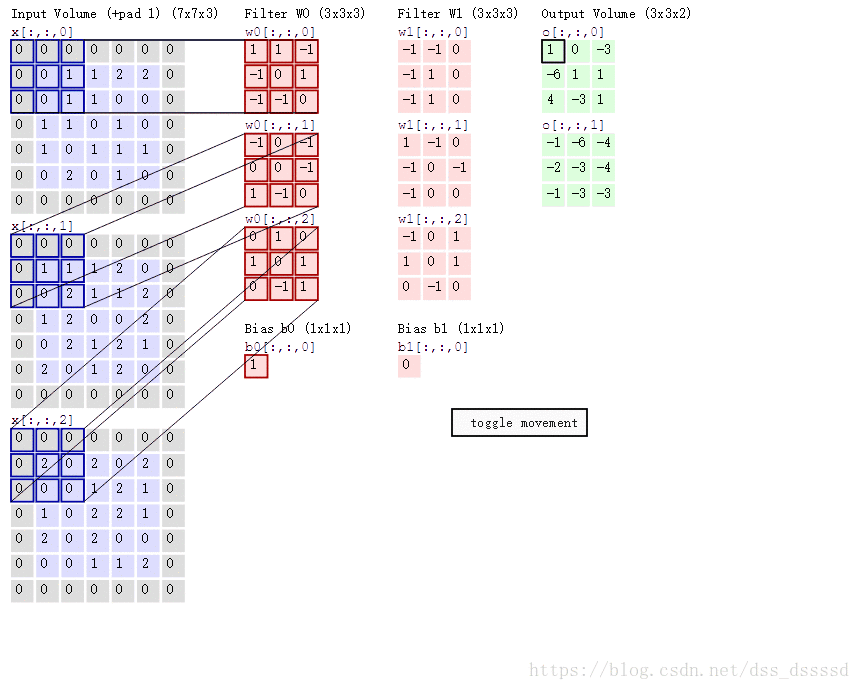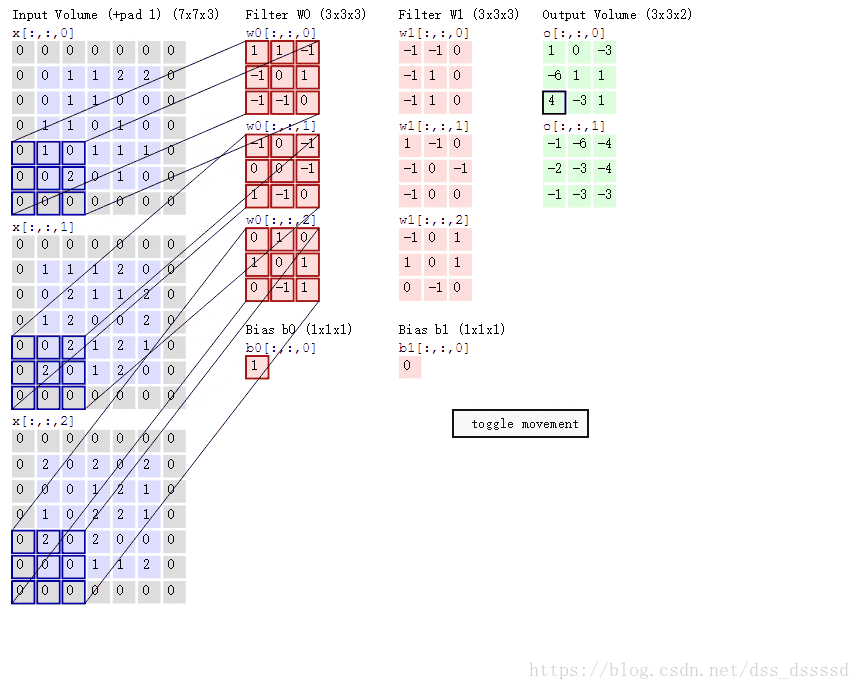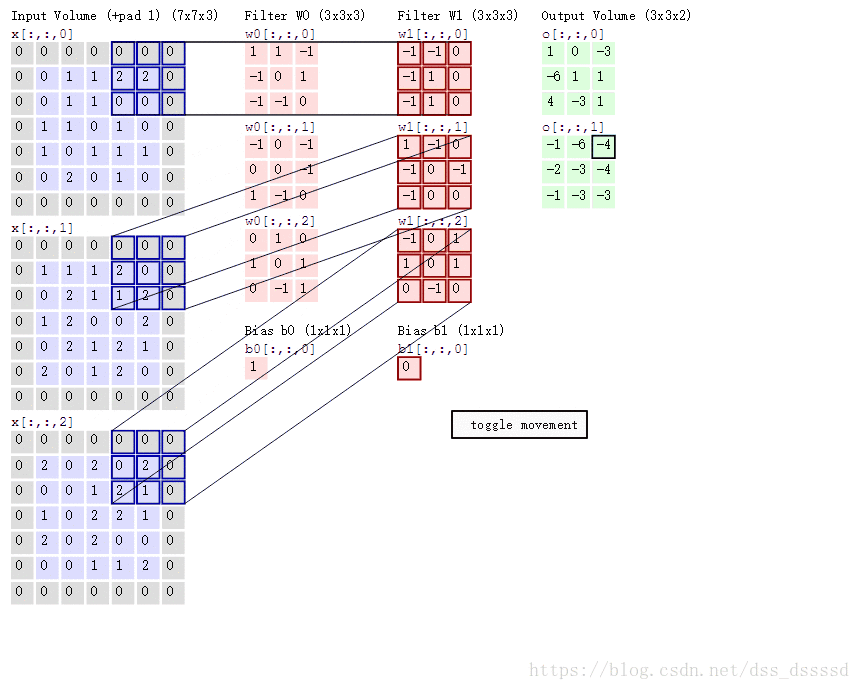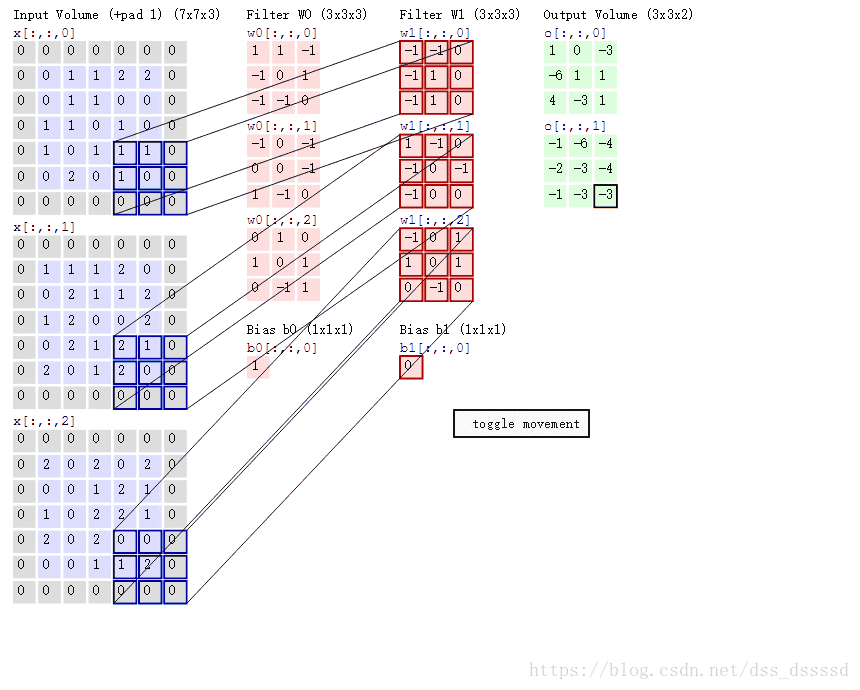
　　卷积的过程为对输入的每个通道与过滤器对应位置相乘后累加，如上图绿色框左上角的第一个值：
　　$$1=(0\times 1+0\times 1+0\times -1+0\times -1+0\times 0+1\times 1+0\times -1+0\times -1+1\times 0)+(\cdots )+(\cdots )+1=1+-1+0+1$$
　　我们肯定不能只在图像中检测一种特征，而是要同时检测水平、垂直、45度边缘等等特征，此时就要使用多个过滤器了。在上面的代码中我们使用了32个过滤器，将单通道的28×28×1图像转成了28×28×32的特征。
　　卷积的权值共享指的是使用的是同一个filter在图像上滑动，而不是每滑动一次换一个filter。

4.激活函数(relu)

conv1 = tf.nn.relu(conv1 + b_c1, name='relu1')  # 使用relu激活函数  

激活函数的作用是增加网络对非线性问题的拟合能力。使用relu函数的优点有以下三点：

• 计算速度快
  　　和sigmod需要计算指数和倒数相比，relu函数只需要计算max(0,x)，速度要快很多。
• 减轻梯度消失的问题
  　　使用bp算法进行梯度计算时，每经过一层sigmod神经元，梯度都要乘以sigmod的导数，最后会导致梯度消失。relu的导数为1，不会导致梯度变小，所以使用relu作为激活函数可以训练更深的网络。
• 稀疏性
  　　使用sigmod函数时，所有的神经元都会被激活，而使用relu函数作为激活函数，一部分的神经元不被激活(输出为0),减少了参数的相互依存关系，缓解了过拟合问题的发生。

5.pooling(池化)

conv1 = tf.nn.max_pool(conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME', name='pool1')
"""
tf.nn.max_pool(
    value,
    ksize,
    strides,
    padding,
    data_format='NHWC',
    name=None
)
    Args:
        input：输入的张量
        ksize：输入张量的每个维度的窗口大小.
        strides：输入张量的每个维度的滑动窗口的步幅.
        padding：一个字符串,可以是'VALID'或'SAME'.填充算法.
"""

池化操作对输入的特征图进行压缩，一方面使特征图变小，简化网络计算复杂度；一方面进行特征压缩，提取主要特征(池化不改变通道数量)。
　　池化操作一般有两种，一种是avy_pool，一种是max_pool，前者是取窗口内的均值(用的较少)，后者是取最大值，如下图所示。
　　
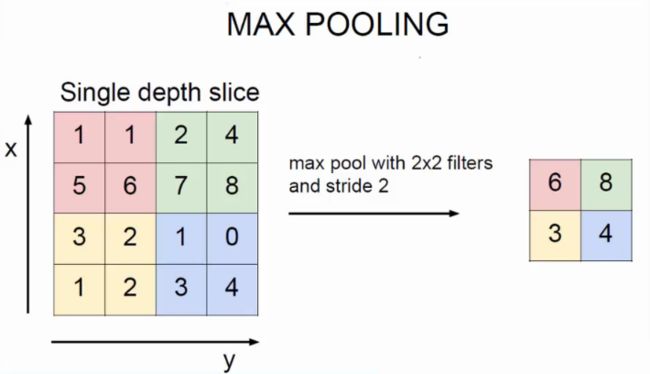
　　在上面的代码中，使用如图所示2×2窗口和移动步长为2的池化操作，将28×28×32的特征图变为了14×14×32的特征图。

6.全连接层

全连接层是一种全连接网络，与MLP(多层感知机)类似，将卷积层输出的3136个特征转成1024个特征，最后转成输出层的10个输出，如下面dropout的图(a)所示。由于每个神经元和相邻层的所有神经元都有连接，所以称之为全连接层。

7.dropout

keep_prob = tf.placeholder(tf.float32)
dense = tf.nn.dropout(dense, keep_prob)

为了减少过拟合，我们在输出层之前加入dropout。keep_prob是一个placeholder，表示神经元保持不变(不被去掉)的概率p。在训练的过程中keep_prob设为0.5，表示在每次训练时每个神经元将有50%的概率被去除(或者叫屏蔽)，即输出为0，但这种去除不是永久性的，只是在当前训练步骤被去除，这样做的目的是减少神经元之间的相互依赖性。在测试时keep_prob设为1，表示保留所有的神经元。dropout的过程如下图所示：

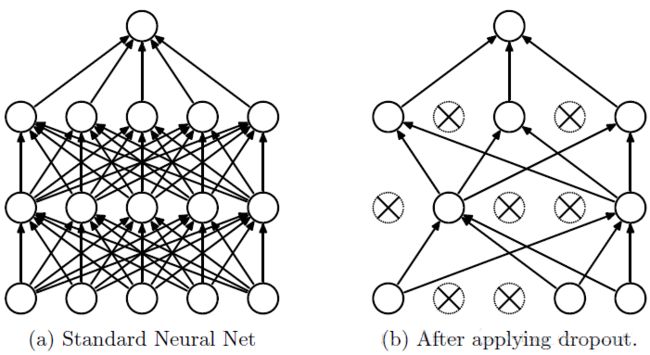
　　由于训练时只使用了一部分神经元，而测试时所有的神经元都参与计算，测试时的输出必然会比训练时大，因此测试时的输出需要乘以神经元不被去掉的概率p，称之为scale。TensorFlow会自动处理输出值的scale，所以在TensorFlow中使用dropout时不需要考虑scale的问题。
　　总结：当前dropout大量应用于全连接网络，在卷积网络隐藏层中由于卷积自身的稀疏化以及稀疏化的ReLu函数的大量使用等原因，Dropout策略在卷积网络隐藏层中使用较少。

8.softmax

softmax函数用来将原来输出层神经元不限制取值范围的10个浮点型输出转为概率输出(取值为[0,1]，且10个概率之和为1)，转化方式为： 　　

$$Si=\frac{e^{zi}}{{\sum }_k{e}^{zk}}$$

　　使用softmax的作用是方便与label求(交叉熵)损失，因为label的形式是概率的。(如"0"的label为{1, 0, 0, 0, 0, 0, 0, 0, 0, 0})。

完整代码

# encoding=utf-8

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('MNIST_data/', one_hot=True)

"""
    输入
"""
with tf.name_scope('input'):
    x = tf.placeholder(tf.float32, [None, 784])
    x_reshape = tf.reshape(x, [-1, 28, 28, 1])
with tf.name_scope('labels'):
    y_ = tf.placeholder(tf.float32, [None, 10])

"""
    第一层卷积层
"""
with tf.name_scope('conv_1'):
    w_c1 = tf.Variable(tf.truncated_normal([5, 5, 1, 32], stddev=0.1), name='w_c1')
    b_c1 = tf.Variable(tf.constant(0.1, shape=[32]), name='b_c1')
    conv1 = tf.nn.conv2d(x_reshape, w_c1, strides=[1, 1, 1, 1], padding='SAME', name='conv1')
    """
    tf.nn.conv2d(
        input,
        filter,
        strides,
        padding
    )
        Args:
            input:  输入的张量
            filter: 过滤器,为变量Tensor(参数需要训练),形状为[filter_高, filter_宽, 输入通道数, 输出通道数]
            strides: 过滤器移动的步长
            padding: 填充算法,有两种方式,分别为"SAME"和"VALID"

    """
    conv1 = tf.nn.relu(conv1 + b_c1, name='relu1')  # 使用relu激活函数
    conv1 = tf.nn.max_pool(conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME', name='pool1')
    """
    tf.nn.max_pool(
        value,
        ksize,
        strides,
        padding,
        data_format='NHWC',
        name=None
    )
        Args:
            input：输入的张量
            ksize：输入张量的每个维度的窗口大小.
            strides：输入张量的每个维度的滑动窗口的步幅.
            padding：一个字符串,可以是'VALID'或'SAME'.填充算法.
    """

"""
    第二层卷积层
"""
with tf.name_scope('conv_2'):
    w_c2 = tf.Variable(tf.truncated_normal([5, 5, 32, 64], stddev=0.1), name='w_c2')
    b_c2 = tf.Variable(tf.constant(0.1, shape=[64]), name='b_c2')
    conv2 = tf.nn.conv2d(conv1, w_c2, strides=[1, 1, 1, 1], padding='SAME', name='conv2')
    conv2 = tf.nn.relu(conv2 + b_c2, name='relu2')  # 使用relu激活函数
    conv2 = tf.nn.max_pool(conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME', name='pool2')

"""
    全连接层
"""
with tf.name_scope('fc'):
    w_d = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1024], stddev=0.1), name='w_d')
    b_d = tf.Variable(tf.constant(0.1, shape=[1024]), name='b_d')
    dense = tf.reshape(conv2, [-1, 7 * 7 * 64])
    dense = tf.matmul(dense, w_d)
    dense = tf.nn.relu(dense + b_d, name='relu_d')
    # 使用Dropout, keep_prob是一个占位符, 训练时为0.5, 测试时为1
    keep_prob = tf.placeholder(tf.float32)
    dense = tf.nn.dropout(dense, keep_prob)

"""
    输出层
"""
with tf.name_scope('output'):
    w_out = tf.Variable(tf.truncated_normal([1024, 10], stddev=0.1), name='w_out')
    b_out = tf.Variable(tf.constant(0.1, shape=[10]), name='b_out')
    y = tf.matmul(dense, w_out) + b_out

loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
optimizer = tf.train.AdamOptimizer(1e-4).minimize(loss)

correct = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())

    tf.summary.FileWriter('logs/', sess.graph)
    for i in range(20000):
        batch = mnist.train.next_batch(50)
        if i % 100 == 0:
            # 每100次输出一次准确率
            acc = sess.run(accuracy, feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.})
            print('step %d, accuracy:%g' % (i, acc))
        # 训练
        sess.run(optimizer, feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

    acc = sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.})
    print('training completed, test accuracy:%g' % acc)

参考资料

[1] https://www.cnblogs.com/zf-blog/p/6075286.html
[2] https://blog.csdn.net/dss_dssssd/article/details/82659316
[3] https://blog.csdn.net/glory_lee/article/details/77899465
[4] https://blog.csdn.net/yjl9122/article/details/70198357

我的博客

如果这些内容对你有所帮助，可以关注我的个人博客哦~
http://www.xyu.ink/blog