机器学习编程作业ex4(matlab/octave实现)-吴恩达coursera
分成两部分，一是本节课程内容的简要回顾，二是作业步骤的推导
程序打包网盘地址提取码1111
一、（Week 5）内容回顾
BP（反向传播）算法：
1.前向传播先计算出当前参数Theta对应的各层每个单元的值a；
2.由输出层的误差计算倒推各个隐藏层的误差delta；
3.利用各层误差delta计算梯度值；
4.利用迭代函数fmincg求出代价函数最小（梯度grad=0）时的theta值，与之前的梯度下降法不断更新theta值类似。
需要编辑以下的红色文件。（后续部分，需要填入的代码为深色框，已经提供的代码为浅色框。）
| 文件 | 内容 |
|---|---|
| ex4.m | 神经网络主程序 |
| ex4data1.mat | 手写数字数据集 |
| ex4weights.mat | 神经网络初始参数 |
| displayData.m | 可视化数据集 |
| fmincg.m | 优化函数 |
| sigmoid.m | sigmoid函数 |
| computeNumericalGradient.m | 梯度计算函数 |
| checkNNGradients.m | 梯度检查函数 |
| debugInitializeWeights.m | 初始化权重函数 |
| predict.m | 准确度预测函数 |
| sigmoidGradient.m | 计算梯度的sigmoid函数 |
| randInitializeWeights.m | 随机化初始权重 |
| nnCostFunction.m | 神经网络误差函数 |
二、作业- Neural Networks 神经网络
ex3利用前馈传播预测手写数字，这部分是利用反向传播Backpropagation即BP算法来识别数字。
2.1 Part 1: Plotting 绘图
这部分同ex3一样，主程序提供加载数据及选取部分数据画图的代码。
input_layer_size = 400;
hidden_layer_size = 25;
num_labels = 10;
displayData(sel);
load(‘ex4data1.mat’);
m = size(X, 1);
% Randomly select 100 data points to display
sel = randperm(size(X, 1));
sel = sel(1:100);
displayData(X(sel, );
| 加载的结果 | 含义 |
|---|---|
| X | 5000*400，某一行代表某个0~9数字对应的400个灰度值 |
| y | 5000*1，每一行对应的手写体数字 |
2.2 Part 2: Loading Pameters加载参数
主函数ex4提供了代价函数接口，如下：
load(‘ex4weights.mat’);
% Unroll parameters
nn_params = [Theta1( ; Theta2(];
加载theta1和theta2的预设参数，其中theta1为25401，theta2为1026
2.3 Part 3: Compute Cost (Feedforward) 计算前向传播的代价项
主函数ex4这部分提供代价函数接口及验证函数准确性：
lambda = 0;
J = nnCostFunction(nn_params, input_layer_size, hidden_layer_size, …
num_labels, X, y, lambda);
fprintf(['Cost at parameters (loaded from ex4weights): %f '…
‘\n(this value should be about 0.287629)\n’], J);
由于之前将theta1和theta2的元素用nn_params合并成一个列向量，因此在nnCostFunction.m函数中先用reshape提取出两个参数矩阵
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), …
hidden_layer_size, (input_layer_size + 1));
Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), …
num_labels, (hidden_layer_size + 1));
% Setup some useful variables
m = size(X, 1);
% You need to return the following variables correctly
J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));
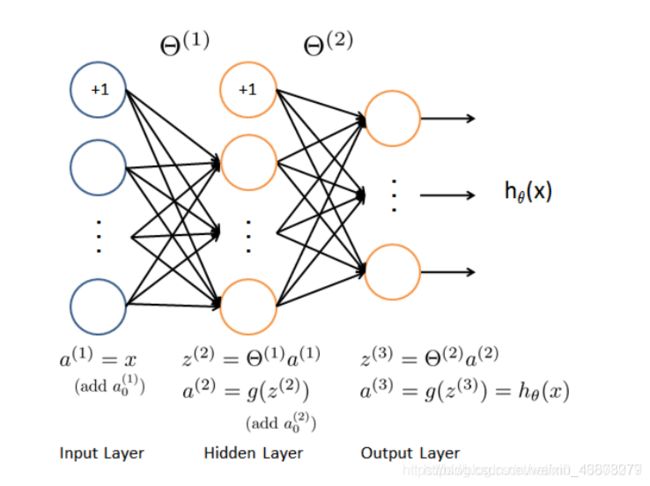与上一节同理，神经网络采取一个具有25个单元的隐藏层，对应的代价函数为：
需要在nnCostFunction.m文件中填入代码：
a1 = [ones(m, 1) X]; %5000x401
z2 = a1 * Theta1'; %5000x25 Theta1 25*401
a2 = sigmoid(z2); %5000x25
a2 = [ones(m, 1) a2]; %5000x26
z3 = a2 * Theta2'; %5000x10 Theta2 10*26
a3 = sigmoid(z3); %5000x10
h = a3; %5000x10
u = eye(num_labels);
y = u(y,:);
J = 1/m*(sum(sum(-y .* log(h) - (1 - y) .* log(1 - h))));
这里采用向量化方式，各个变量的矩阵大小已经在代码中标出，由此即可计算出代价函数值。
2.4 Part 4: Implement Regularization 实现正则化
主函数
lambda = 1;
J = nnCostFunction(nn_params, input_layer_size, hidden_layer_size, …
num_labels, X, y, lambda);
fprintf(['Cost at parameters (loaded from ex4weights): %f '…
‘\n(this value should be about 0.383770)\n’], J);
加入正则项之后的代价函数为：
在2.3的基础上，继续在nnCostFunction.m文件中填入代码：
regularization = lambda/(2 * m) * (sum(sum(Theta1(:,2:end) .^ 2)) + sum(sum(Theta2(:,2:end) .^ 2)));
J = J + regularization;
需要注意，因为正则项regularization的第一项对应输入的特征量1，因此，约定俗成，在这里只选取2:end进行计算。
2.5 Part 5: Sigmoid Gradient
主函数提供sigmoid验证函数接口，
fprintf(’\nEvaluating sigmoid gradient…\n’)
g = sigmoidGradient([-1 -0.5 0 0.5 1]);
fprintf('Sigmoid gradient evaluated at [-1 -0.5 0 0.5 1]:\n ‘);
fprintf(’%f ', g);
同之前几节，sigmoid函数定义及求导特点如下：
因此，主函数BP算法需要调用求得sigmoid导数时，填入以下代码：
g = sigmoid(z) .* (1 - sigmoid(z));
在这里，z为任意矩阵，因此计算每个元素的导数，需要用 .*的形式。
2.6 Part 6: Initializing Pameters 初始化参数
主函数提供了初始化
initial_Theta1 = randInitializeWeights(input_layer_size, hidden_layer_size);
initial_Theta2 = randInitializeWeights(hidden_layer_size, num_labels);
% function W = randInitializeWeights(L_in, L_out)
% Unroll parameters
initial_nn_params = [initial_Theta1(: ) ; initial_Theta2(: )];
在randInitializeWeights.m文件中填入下列代码:
epsilon_init = 0.12;
W = rand(L_out, 1 + L_in) * (2 * epsilon_init) - epsilon_init;
rand随机产生0到1的数，经过处理后为-ε到ε。（这部分代码在帮助pdf文件中已经给出）
2.7 Part 7: Implement Backpropagation 反向传播算法
checkNNGradients;
function checkNNGradients(lambda)
%lambda未赋值时，进行默认赋值
if ~exist(‘lambda’, ‘var’) || isempty(lambda) %isempty() 为判断数列是否为空的程序，而0元素不是空元素，如lambda未被赋值，输出为1，lambda=0输出为0
lambda = 0;
end
%创建的小型数据集，验证梯度检验函数的正确性
input_layer_size = 3;
hidden_layer_size = 5;
num_labels = 3;
m = 5;
% We generate some ‘random’ test data 返回一组sin( 1~size(W) )的初始值
Theta1 = debugInitializeWeights(hidden_layer_size, input_layer_size);
Theta2 = debugInitializeWeights(num_labels, hidden_layer_size);
% Reusing debugInitializeWeights to generate X
X = debugInitializeWeights(m, input_layer_size - 1);
y = 1 + mod(1:m, num_labels)’; %mod取余运算，y输出为2 3 1 2 3
% Unroll parameters
nn_params = [Theta1(: ) ; Theta2(: )];
% Short hand for cost function
costFunc = @§ nnCostFunction(p, input_layer_size, hidden_layer_size, …
num_labels, X, y, lambda);
[cost, grad] = costFunc(nn_params); %存储用反向传播计算出的偏导数项
numgrad = computeNumericalGradient(costFunc, nn_params);%存储利用数值检验求出的偏导项
% Visually examine the two gradient computations. The two columns
% you get should be very similar.
disp([numgrad grad]);
diff = norm(numgrad-grad)/norm(numgrad+grad); %比较两者的差异
这里反向传播计算偏导：
之前nnCostFunction.m中只填入了计算代价部分的代码，因此，接下来需要填入反向传播计算偏导的代码：
delta3 = a3 - y; % 5000 * 10
delta2 = delta3 * Theta2; % 5000 * 26
delta2 = delta2(:,2:end); % 5000 * 25
delta2 = delta2 .* sigmoidGradient(z2); % 5000 * 25
Delta1 = zeros(size(Theta1)); % 25 * 401
Delta2 = zeros(size(Theta2)); % 10 * 26
Delta1 = Delta1 + delta2' * a1; % 25 * 401 5000×25' * 5000x401
Delta2 = Delta2 + delta3' * a2; % 10 * 26 5000×10' * 5000x26
Theta2_grad = 1/m * Delta2;
Theta1_grad = 1/m * Delta1;
如上，同样是考虑向量化，按照反向传播思路，之前已经按照前向传播计算出a2、a3，我们现在先计算delta3，利用这个误差值计算前一层的误差delta2，由此计算出偏导。
数值检验计算偏导项是利用了导数定义。
向量化中，需要进行如下n个梯度的操作：
2.8a Part 8: Implement Regularization 加入正则化
主函数提供了lambda=3时的正则化代价函数接口，如下：
lambda = 3;
checkNNGradients(lambda);
% Also output the costFunction debugging values
debug_J = nnCostFunction(nn_params, input_layer_size, …
hidden_layer_size, num_labels, X, y, lambda);
fprintf([’\n\nCost at (fixed) debugging parameters (w/ lambda = %f): %f ’ …
‘\n(for lambda = 3, this value should be about 0.576051)\n\n’], lambda, debug_J);
与之前类似，正则化只给theta从第二项开始，如下所示：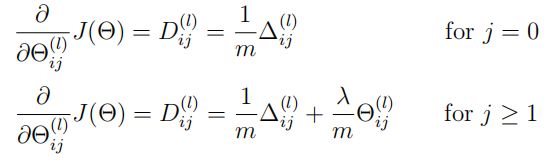
因此，需要在nnCostFunction.m中填入代码：
Theta1_temp = Theta1;
Theta1_temp(:, 1) = 0;
Theta2_temp = Theta2;
Theta2_temp(:, 1) = 0;
Theta1_grad = Theta1_grad + lambda / m * Theta1_temp;
Theta2_grad = Theta2_grad + lambda / m * Theta2_temp;
本部分先对theta矩阵的第一列赋值为0，实现只从第二项开始的正则化：
j（第一列）=1的时候lambda / m * Theta1_temp为0，Theta1_grad = Theta1_grad；
j（第一列）不等于1的时候，Theta1_grad = Theta1_grad + lambda / m * Theta1_temp;
2.8b Part 8: Training NN 训练神经网络
options = optimset(‘MaxIter’, 50);
% You should also try different values of lambda
lambda = 1;
% Create “short hand” for the cost function to be minimized
costFunction = @§ nnCostFunction(p, …
input_layer_size, …
hidden_layer_size, …
num_labels, X, y, lambda);
[nn_params, cost] = fmincg(costFunction, initial_nn_params, options);
% Obtain Theta1 and Theta2 back from nn_params
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), …
hidden_layer_size, (input_layer_size + 1));
Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), …
num_labels, (hidden_layer_size + 1));
同之前类似，这里利用fmincg函数求出代价函数costFunction最小时的theta参数值。
2.9 Part 9: Visualize Weights 可视化权重
fprintf(’\nVisualizing Neural Network… \n’)
displayData(Theta1(:, 2:end));
其中，Theta1参数矩阵25* 401（25代表25个隐藏层单元，401为包括了x0=1的401个输入参数，实际展示只计算2：end的400个输入参数）。
displayData函数就是将每个单元的400个输入参数利用imagesc(display_array, [-1 1])函数将display_array矩阵（20*20）每个元素的值变成RGB/灰度值输出，即图像→数据的逆运算。输出如下所示：
2.10 Part 10: Implement Predict 准确度计算
pred = predict(Theta1, Theta2, X);
fprintf(’\nTraining Set Accuracy: %f\n’, mean(double(pred == y)) * 100);
跟之前一样，利用训练得到的Theta1、Theta2值计算输出的预测值向量pred，然后将其与实际输入y比较，得到准确度。
参考资料
吴恩达机器学习（十）—— ex4：Neural Networks Learning（MATLAB+Python）
Matlab吴恩达机器学习编程练习ex4：神经网络Neural Networks Learning
吴恩达机器学习第五周学习笔记及编程作业答案