2022宁夏杯B题论文分析+完整代码(大学生就业问题分析)
写这篇博客只是梳理一下宁夏杯的思路,仅供参考
本篇博客代码和论文来源于:CSDN的Day-3博主,已征得本人统一,感谢Day-3大佬。
文章目录
- 一、题目
- 二、摘要
- 三、问题分析
-
- 3.1问题一分析
- 3.2问题二分析
- 3.3问题三分析
- 四、模型假设
- 五、模型的建立与求解
-
- 5.1 数据处理与分析
- 5.2 问题一的模型
-
- 5.2.1 数据分析模型
- 5.2.2 皮尔逊相关系数模型
- 5.2.3 随机森林模型
- 5.2.4 加权评价
- 5.3 问题二的模型
-
- 5.3.1 方差膨胀因子
- 5.3.2 多元线性回归模型
- 5.3.3 岭回归模型
- 5.3.4 求解
- 5.4 问题三求解
- 六、模型评价与推广
-
- 6.1 模型的优点
- 6.2 模型的缺点和改进
- 七、代码
-
- 1、数据预处理
- 2、模型建立
-
- 【1】岭回归
- 【2】随机森林
- 【3】多元线性回归
- 3、影响Salary的因素
一、题目
| 属性 | 说明 |
|---|---|
| ID | 用于识别候选人的唯一ID |
| 薪金 | 向候选人提供的年度CTC(以INR为单位) |
| 性别 | 候选人的性别 |
| DOB | 候选人的出生日期 |
| 10% | 在10年级考试中获得的总成绩 |
| 10board | 10年级时遵循其课程的校务委员会 |
| 12毕业 | 毕业年份-高中 |
| 12% | 在12年级考试中获得的总成绩 |
| 12board | 候选人遵循其课程的校务委员会 |
| CollegeID | 唯一ID,用于标识候选人为其大学就读的大学/学院 |
| CollegeTier | 每所大学都被标注为1或2。标注是根据该学院/大学学生获得的平均AMCAT分数计算得出的。平均分数高于阈值的大学被标记为1,其他被标记为2。 |
| 学位 | 候选人获得/追求的学位 |
| 专业化 | 候选人追求的专业化 |
| CollegeGPA | 毕业时的GPA总计 |
| CollegeCityID | 唯一的ID,用于标识学院所在的城市。 |
| CollegeCityTier | 学院所在城市的层。这是根据城市人口进行注释的。 |
| CollegeState | 学院所在州的名称 |
| 毕业年份 | 毕业年份(学士学位) |
| 英语 | AMCAT英语部分中的分数 |
| 逻辑 | 在AMCAT逻辑能力部分中得分 |
| 数量 | 在AMCAT的“定量能力”部分中得分 |
| 域 | AMCAT域模块中的分数 |
| ComputerProgramming | AMCAT的“计算机编程”部分中的得分 |
| ElectronicsAndSemicon | AMCAT的“电子和半导体工程”部分得分 |
| 计算机科学 | 在AMCAT的“计算机科学”部分中得分 |
| MechanicalEngg | AMCAT机械工程部分中的得分 |
| ElectricalEngg | AMCAT的电气工程部分中的得分 |
| TelecomEngg | AMCAT的“电信工程”部分中的得分 |
| CivilEngg | AMCAT的“土木工程”部分中的得分 |
| 尽职调查 | AMCAT人格测验之一的分数 |
| 一致性 | AMCAT人格测验之一的分数 |
| 外向性 | AMCAT人格测验之一的分数 |
| 营养疗法 | AMCAT人格测验之一的分数 |
| 开放性到经验 | 分数在AMCAT的个性测试的部分之一 |
二、摘要
随着高等院校学生数量的日益增多,毕业生们的就业率倍受重视。因为受到了社会环境和疫情等各种因素的影响,大学生们的就业机会大大增加,而且大学生们的薪酬的待遇水平也不一样,从而分析各种因素对大学毕业生工资的影响程度大小,就变得尤为重要。
针对问题一, 分析影响高校工程类专业毕业生就业的主要因素,首先,使用Python进行数据分析与可视化,对各种因素与Salary的关系进行可视化处理,便于直观的感受各种因素与Salary的关系;其次,建立皮尔逊相关系数模型和随机森林计算权重模型,列出相关性和权重较大的因素;最后,建立加权评价模型,对两种模型的结论进行加权求和,得到最终结论。Quant、Logical、English、12percentage、Domain、ComputerProgramming、agreeableness这几种因素是影响高校工程类专业毕业生就业的主要因素。
针对问题二, 刻画工程类专业毕业生薪水和各因素的关系,引入多元回归方程模型和岭回归模型,将拟合的回归方程中各个因素的系数作为衡量该因素与Salary关系的依据,最后得到的系数数组可以准确的表达各因素与工程类大学毕业生薪水的关系。当系数为正数,则该因素与Salary呈正相关关系,该因素的值越大,则Salary的值越大,该因素的系数越大,则该因素的Salary的影响越大;当系数为负数,则该因素与Salary呈负相关关系,该因素的值越小,则Salary的值越大,该因素的系数越小,则该因素的Salary的影响越大。系数数组保存在附件中的‘多元线性回归coal.xlsx’和‘岭回归coal.xlsx’中。
针对问题三, 结合问题一和问题二的结论,和自己的真切感受,为自己所在的高校写一份咨询建议,表明自己对工程类大学生培养的见解。
关键字: 数据分析与可视化,皮尔逊相关系数,随机森林,加权评价,多元线性回归,岭回归。
三、问题分析
3.1问题一分析
问题一要求我们分析影响高校工程类专业毕业生就业的主要因素。我们可以使用一些相关性公式来计算,例如皮尔逊相关系数或者斯皮尔曼相关系数等;其次我们也可以使用随机森林中这种算法来求出各个因素的重要程度。
3.2问题二分析
问题二要求我们刻画工程类专业毕业生薪水和各因素的关系。我们可以使用回归类模型对各个因素与薪水的关系进行拟合,以斜率值的正负大小确定工程类毕业生薪水和各因素的关系。
3.3问题三分析
问题三要求我们根据在问题一、二中得到的结论,为自己所在的高校写一份关于高校工程类专业学生培养的咨询建议。
四、模型假设
1.不考虑因货币增值或者贬值影响毕业大学生的薪水
2.不考虑因政治因素影响社会局势从而影响毕业生的薪水。
3.忽略毕业生薪水的短期涨跌。
4.假设所给数据真实可信。
5.不考虑其他外界因素影响各因素之间的关系。
定义与符号说明:
| 符号 | 定义 |
|---|---|
| Z | z-score的得分值 |
| r | 皮尔逊相关系数 |
| Qi | 最终评价系数 |
| Ii | 随机森林重要程度系数 |
五、模型的建立与求解
5.1 数据处理与分析
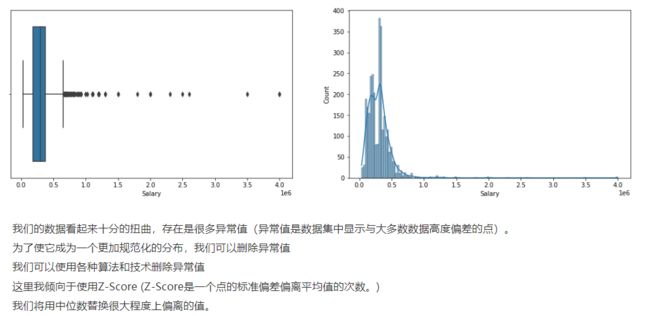
首先,根据题目中所给的资料,查看薪金Salary的分布情况。根据资料综合分析得到了Salary分布情况图表,如下图所示。

通过图片可以知道,这些数据明显存在很多异常值(异常值是数据集中显示与大多数数据高度偏差的点),难以让我们进行更深层次的数据分析。为了使它成为一个更加规范化的分布,我们可以删除其中的异常值,从而保证数据的正常性。在这里我们使用Z-Score,先寻找出中位数,通过筛选找到这些异常值,并使用中位数替换这些偏离程度大的异常值。
z-score 也叫 standard score,通过分析数据,用于评估样本点到总体均值的距离,判断这些数据是否标准。z-score主要的应用是测量原始数据与数据总体均值相差多少个标准差。计算公式如下:
z = X ‾ − u σ / n (1) z=\frac{\overline{X}-u}{σ/\sqrt{n}} \tag{1} z=σ/nX−u(1)
在这组数据中,当薪资的z-score大于3时,我们将其替换为中位数以保证数据的正常性。
最后,通过z-score技术的修改完善后,Salary的分布状况如图表 2 所示,我们可以看到Salary基本符合正态分布,大部分大学生的薪资处于200k到400k之间,只有少数部分的薪资为600K甚至800K,通过这些数据我们可以进行近一步的数据分析。

在课程成绩的因素中,-1代表学生没有选这门课,通过数据发现,没有选课的大学生的薪资和有选这门课的大学生的薪资是没有什么大体的规律的。因此为了方便起见,我们将-1转换成0,表示此模块对Salary没有任何贡献。
查看性别Gender的数量统计与Gender与Salary的关系,如下图 所示,我们可以发现,男性和女性的比例大约为4:1,但是Gender与Salary并没有明显的关系,因此我们可以知道,性别对薪资的影响是不大的。

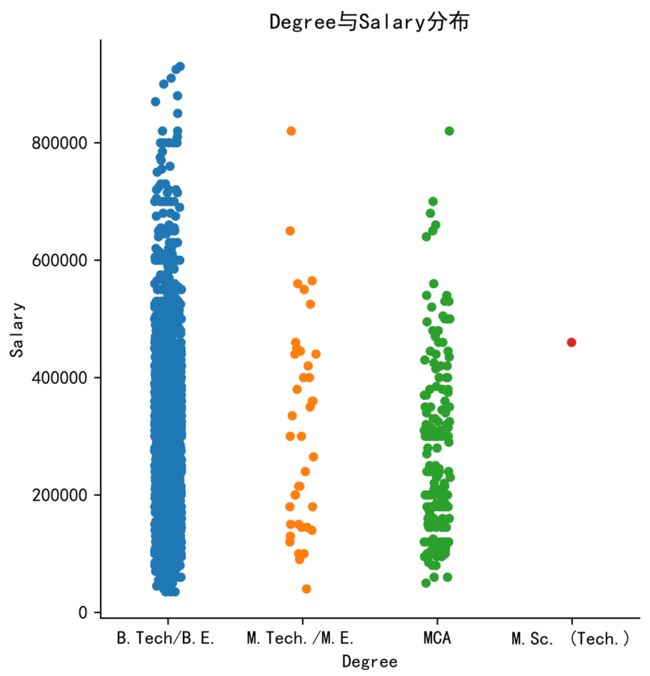
查看Degree的分布情况对于薪资的影响,我们进行了数据的分析处理,最后得到结果,如图表 4所示。大部分Degree为B.Tech/B.E,只有极少数为MCA、M.Tech/M.E和M.Sc(Tech)。
- B.Tech/B.E:本科学位(理科学士)
- MCA:计算机应用程序硕士
- M.Tech/M.E:工程硕士
- M.Sc(Tech):理学硕士
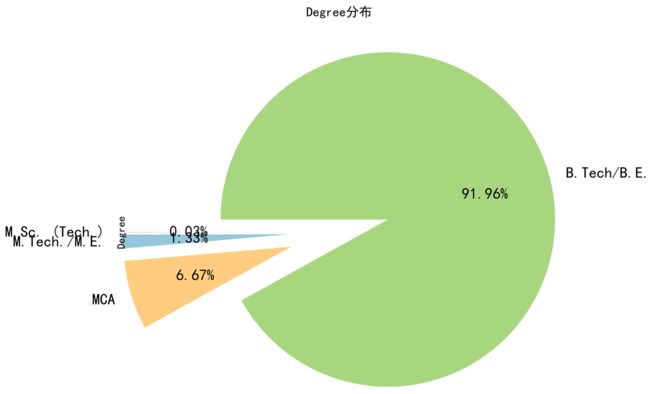
然后我们根据这些数据,与薪资相结合,进行了数据分析,得到了Degree与Salary的相关系,如下图所示。在下图中,Degree为B.Tech/B.E的大学生中,薪资主要集中在在40K到600K,600K到900K也比较多,但是相比之下,M.Tech/M.E与MCA在600K到800K的大学生只有少数几个,然而M.Sc(Tech)的大学生薪资在400K上。因此我们可以得出结论大学生Degree对薪资的影响是比较大的。
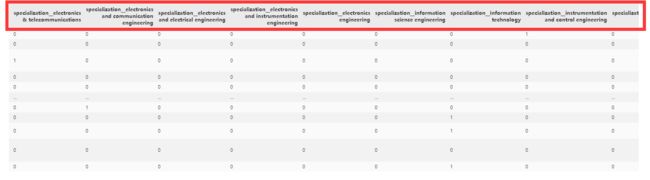
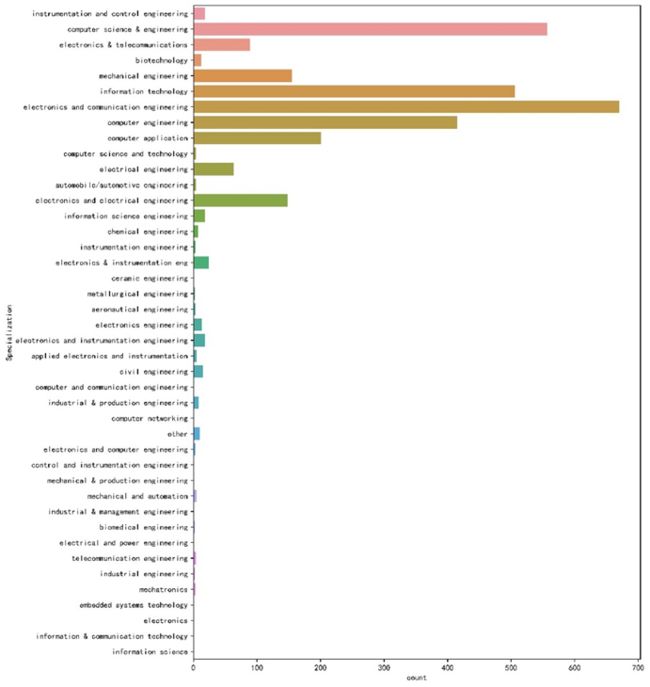
对Specialization进行数量统计,如下图所示。数量最多的有computer science&engineering、information technology、electronics and communication engineering和computer engineering这四种,其他的数量较少。
图表 : S p e c i a l i z a t i o n 数量统计 图表 :Specialization数量统计 图表:Specialization数量统计
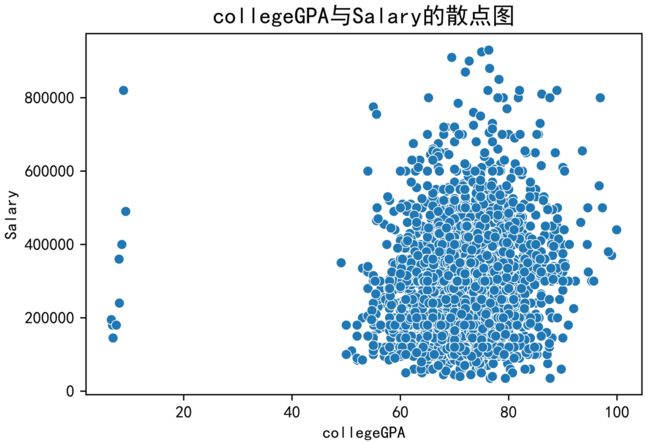
根据数据来绘制12percentage与CollegeGPA的散点图,如下图所示,我们可以看到有少量的异常值,这些异常值会影响我们正常的数据分析,我们将CollegeGPA较低的少量数值删除。
查看ColleageGPA与Salary的散点图,如下图所示。将ColleageGPA较小的异常值也剔除。
5.2 问题一的模型
5.2.1 数据分析模型
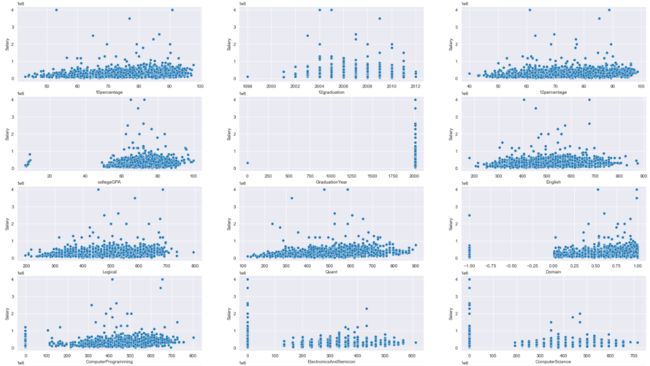
通过数据分析,我们得到了一些新的数据,可以对我们的问题进行解决。下图表10所示为10percentage, 12graduation, 12percentage, collegeGPA, GraduationYear,English,Logical,Quant,Domain,ComputerProgramming,ElectronicsAndSemicon,ComputerScience,MechanicalEngg,ElectricalEngg,TelecomEngg,CivilEngg,conscientiousness,agreeableness,extraversion,nueroticism,openess_to_experience与Salary的关系。通过观察这些图,我们可以得到一些启发,这些因素和Salary都有着不同的关系,我们可以近一步进行分析,去得到一些更准确的这些因素与Salary的关系。
图表 10 : 各因素与 S a l a r y 的散点图 图表 10 :各因素与Salary的散点图 图表10:各因素与Salary的散点图



根据题目中所给的一些数据,我们进行了大量的数据分析,通过电脑的运行分析,我们得到了一个反应这些数据的图表,下面图表11为specialization与Salary的关系的箱型图。根据下图我们可以得知,这些数据中是存在一些异常值的,这些异常值与中位数的差异是非常大的,我们为了数据研究的准确性,将这些异常值进行删除。再次仔细观察这幅图表,这些因素对于Salary的关系的中位数各不相同,他们的上下限也存在差异。
图表 11 : s p e c i a l i z a t i o n 与 S a l a r y 的关系的箱型图 图表11 :specialization与Salary的关系的箱型图 图表11:specialization与Salary的关系的箱型图

5.2.2 皮尔逊相关系数模型
两个变量之间的皮尔逊相关系数定义是通过两个变量之间的协方差和标准方差的商求得的:

上面的式子定义了总体相关系数,通常使用希腊小写字母ρ作为其代表符号。通过估算样本的协方差和标准差,我们可以得到皮尔逊相关系数,该系数常用使用英文小写字母r表示:

由皮尔逊系数,我们把数据带入该式子,通过大量的数据分析,我们可以得到各因素的相关因素,如图表 11所示。
图表 11 :特征间的皮尔森相关系数 图表 11:特征间的皮尔森相关系数 图表11:特征间的皮尔森相关系数
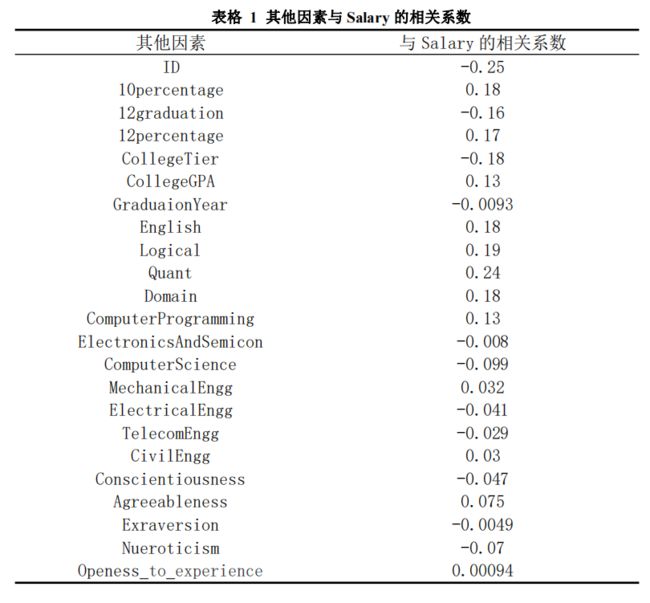
根据这些特征间的皮尔逊相关系数,为了更加直观清晰的得到我们想要的结果,更加清楚的解决问题,我们对这些数据进行了简化,将与Salary有关的因素与Salary的相关系数进行组合分析,得到了其他因素与Salary的相关系数,如下表格 1所示。
5.2.3 随机森林模型
随机森林是在bagging树和决策树之上实现的,两者都得到了改进。随机森林中使用的弱学习器是决策树,没有依赖关系,可以并行生成。正常决策树通过从节点上的所有n个样本特征中选择最好的来拆分决策树,而随机森林选择节点上特征的子集(特征数小于选择的特征数越少,模型越稳健。)
然后从随机选择的特征子集中选择最佳特征,并进行树分割(两层选择),以进一步提高模型的泛化能力。 然后在随机选择的部分特征中选择一个最优的特征来进行树的分割(双层选择),这样可以进一步增强模型的泛化能力。
最后我们得到了各个因素的重要性。我们为了更加直观的观看数据,选中了较大的前二十个数据做成了表格。
5.2.4 加权评价
设各个因素皮尔逊相关系数为 r i r_i ri ,各个因素的随机森林重要程度为 I i I_i Ii ,最终评价系数为 Q i Q_i Qi ,
Q i = r i W 1 + I i W 2 W 1 + W 2 (1) Q_i=\frac{r_iW_1+I_iW_2}{W_1+W_2} \tag{1} Qi=W1+W2riW1+IiW2(1)
其中:
W 1 = ∑ i = 1 n r i (2) W_1=\sum_{i=1}^n r_i \tag{2} W1=i=1∑nri(2)
W 2 = ∑ i = 1 m Q i (3) W_2=\sum_{i=1}^m Q_i \tag{3} W2=i=1∑mQi(3)
我们将两种方式得到的数据进行加权平均,最终得到一组新的数据,如下表所示:

由上图可以的得知,影响Salary的主要因素中比较大的有:Quant、Logical、English、12percentage、Domain、ComputerProgramming、agreeableness。这几个因素分别是在AMCAT的“定量能力”部分中的分数、在AMCAT“逻辑能力”部分中分数、在AMCAT“英语”部分中的分数、在12年级考试中获得的总成绩、在AMCAT网络操作系统模块中的分数、在AMCAT的“计算机编程”部分中的分数、在AMCAT“亲和性”部分中的分数。
综上所述,影响高校工程类专业毕业生就业的主要因素有Quant、Logical、English、12percentage、Domain、ComputerProgramming、agreeableness,这些翻译成中文为在AMCAT的“定量能力”部分中的分数、在AMCAT“逻辑能力”部分中分数、在AMCAT“英语”部分中的分数、在12年级考试中获得的总成绩、在AMCAT网络操作系统模块中的分数、在AMCAT的“计算机编程”部分中的分数、在AMCAT“亲和性”部分中的分数。
5.3 问题二的模型
5.3.1 方差膨胀因子
方差膨胀因子是计算多元回归模型中一种共线性严重程度的度量值。它表示回归系数估计量的方差和假设自变量间不线性相关时方差相比的比值。方差膨胀因子的计算公式为:
V I F i = 1 1 − R i 2 (4) VIF_i=\frac{1}{1-R_i^{2}} \tag{4} VIFi=1−Ri21(4)
根据图片分析,我们可以得知,10 percentage和12percentage之间有高度相关性,此外,VIF值还具有高多重共线性。因此,我们仅使用12percentage。因为与10percentage相比,12percentage更重要,更能够体现共线性。
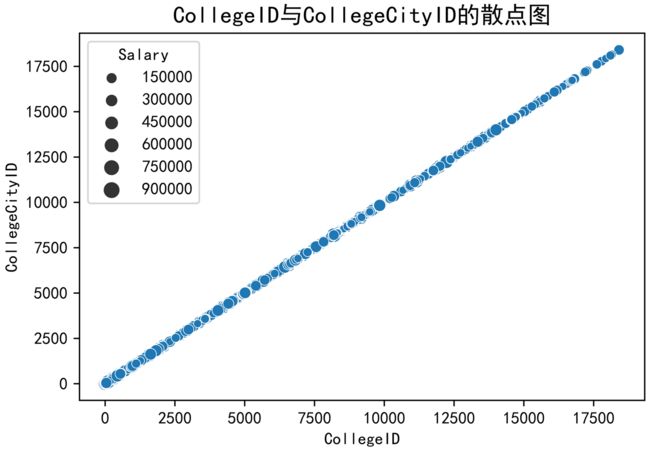
根据资料,我们分析数据,绘制CollegeID与CollegeCityID的散点图,如下图所示。
C o l l e g e I D 与 C o l l e g e C i t y 的散点图 CollegeID与CollegeCity的散点图 CollegeID与CollegeCity的散点图
由图片可知, CollegeID 和 CollegeCityID 对于每个值都是近似相同的,并且它们还的VIF值趋向于正无穷,所以我们有必要删除其中之一。
再次根据资料分析数据,我们绘制10board与12board的散点图,如下图所示。
10 b o a r d 与 12 b o a r d 的散点图 10board与12board的散点图 10board与12board的散点图
虽然10board和12board不是非常相似,但为了减少多重共线性的风险,我们仍然删除10board。
最后,我们绘制了CollegeTier和CollegeCityTier的散点图,如下图所示。
C o l l e g e T i e r 和 C o l l e g e C i t y T i e r 的散点图 CollegeTier和CollegeCityTier的散点图 CollegeTier和CollegeCityTier的散点图

通过图片,我们可以直观的看出CollegeCityTier不如CollegeTier那样相关,所以我们删除CollegeCityTier因素。
5.3.2 多元线性回归模型
线性回归是回归类的数学模型,是用来确定两种及以上变量间的定量关系的一种方法。它的表达形式如下:
y = w x + e (5) y=wx+e \tag{5} y=wx+e(5)
e为误差服从均值为 0 的正态分布。回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。一般来说,线性回归一定可以通过最小二乘法或梯度下降法求出其方程,可以计算出对于 y=bx+a 的直线。以最小二乘法为例一般地,通常影响 y 的因素往往不止一个,所以我们假设有 x1,x2,…,xk,k 个因素,通常可考虑如下的线性关系式:
y = β 0 + β 1 X 1 + β 2 X 2 + . . . + β k X k + ε (6) y=β_0+β_1X_1+β_2X_2+...+β_kX_k+ε \tag{6} y=β0+β1X1+β2X2+...+βkXk+ε(6)
5.3.3 岭回归模型
岭回归(Ridge Regression)是回归方法的一种,属于统计方法。在机器学习中也称作权重衰减。也有人称之为 Tikhonov 正则化。岭回归主要解决的问题是两种:一是当预测变量的数量超过观测变量的数量的时候(预测变量相当于特征,观测变量相当于标签),二是数据集之间具有多重共线性,即预测变量之间具有相关性。
一般的,回归分析的(矩阵)形式如下:
y = ∑ j = 1 p β j X j + β 0 (7) y=\sum_{j=1}^p β_jX_j+β_0 \tag{7} y=j=1∑pβjXj+β0(7)
5.3.4 求解
我们将方程的系数作为判断各个因素与Salary关系的依据。当系数为正数,则该因素与Salary呈正相关关系,该因素的值越大,则Salary的值越大,该因素的系数越大,则该因素的Salary的影响越大;当系数为负数,则该因素与Salary呈负相关关系,该因素的值越小,则Salary的值越大,该因素的系数越小,则该因素的Salary的影响越大。
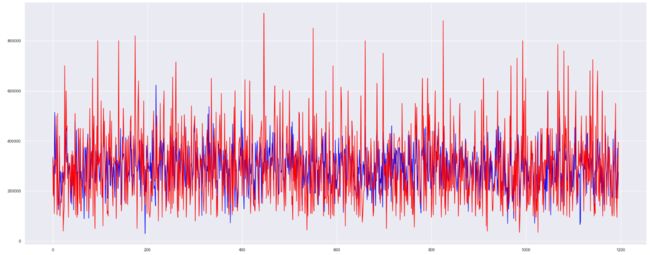
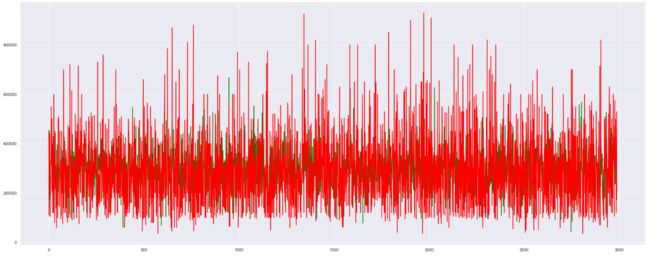
本文提供了两种方案,一种是多元线性回归拟合,另一种是岭回归拟合,如下所示,各因素与Salary的关系一目了然。
多元线性回归拟合图像 多元线性回归拟合图像 多元线性回归拟合图像

5.4 问题三求解
对于各大高校,要坚持立德树人是根本导向的理念,坚定人才培养是根本任务,质量是生命线,教学是中心工作的理念,积极推进教学改革,大力加强专业建设。对于高校的工科生培养,我有以下五条建议。
第一条,培养工科生的定量能力和逻辑能力。关于定量能力和逻辑能力,尽管处理大数据需要大量使用技术,但是任何数据分析的基础都是对统计和线性代数的深入了解。统计学是数据科学的基本组成部分,如果想要分析数据,那么对摘要统计,概率分布,随机变量等核心概念的理解就很重要。这些核心概念需要很大程度上的定量和逻辑分析能力。
尽管传统的数据分析员可能不需要一个成熟的程序员就可以摆脱困境,但是大数据分析员需要非常熟悉编码。主要原因之一是大数据仍处于发展阶段。围绕大数据分析师必须处理的大型复杂数据集设置的标准流程并不多。每天都需要大量定制以处理非结构化数据。
第二条,为工科生开设编程语言的科目。大数据分析需要懂得语言如R,Python,Java,C ++,Ruby,SQL,Hive,SAS,SPSS,MATLAB,Weka,Julia和Scala等计算机编程语言。语言不应该成为工科生就业和完成任务的障碍。至少需要了解R,Python和Java。在工作时,工科生可能最终会使用各种工具。编程语言仅是一种工具,而且在知识储备中拥有更多工具,这是更好的选择。
第三条,督促工科生学号网络操作系统。网络操作系统是一种能代替操作系统的软件程序,是网络的心脏和灵魂,是向网络计算机提供服务的特殊的操作系统。借由网络达到互相传递数据与各种消息,分为服务器(Server)及客户端(Client)。而服务器的主要功能是管理服务器和网络上的各种资源和网络设备的共用,加以统合并控管流量,避免有瘫痪的可能性,而客户端就是有着能接收服务器所传递的数据来运用的功能,好让客户端可以清楚的搜索所需的资源。这无疑是作为一个工科生所必备的武器。
第四条,注重提高工科生的英语水平。编程语言也好,一些先进的工科文献也好,很多都是引自国外学者的论文,如果不具备英语能力,对于科技前沿的知识不能很好的跟随,面对日新月异发展的现在,工科生如果英语落后,就会拉开信息差,从而在技术上导致落后于人。
第五条,开展集体活动培养工科生的亲和力。人际关系中亲和力的重要性亲和力对一个人的人际交往至关重要,这也是那些在很多方面并不出色,却拥有众多朋友的一个重要原因,亲和力同样对工作也会产生积极影响。我们印象中的工科生都是相对来说不善言辞,一门心思搞科研的形象,如果有了一定的亲和性,就会在相对沉默寡言的竞争者中脱颖而出,更具有得到职位的可能。
六、模型评价与推广
6.1 模型的优点
在问题一中,通过多种数据分析方式、作图方式直观的展示数据,有助于发现数据中的特殊关系;使用多种相关性分析方法,并进行综合评价,结论可信度更高。
在问题二中,使用岭回归和逻辑回归模型对问题进行求解,并以各因素的系数作为判断各因素与Salary关系的依据,具有切实可行性。
6.2 模型的缺点和改进
模型的R2评分较低,均方误差较大,需要数据量更大、包含因素更多的数据集,便于进行模型拟合。
七、代码
---------------------------------------------------------------------------------------------代码部分------------------------------------------------------------------------------------
1、数据预处理
# 导入响应模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# 不显示警告
import warnings
warnings.filterwarnings('ignore')
data = pd.read_csv('./B题附件.csv')
data.head()
data.isnull().sum()
全部都是0,没有缺失值。
%matplotlib inline
plt.figure(figsize = (18,5))
plt.subplot(1,2,1)
sns.boxplot(x = 'Salary', data = data)
plt.subplot(1,2,2)
sns.histplot(x = 'Salary', data = data, kde = True)
plt.savefig('C:/Users/LENOVO/Desktop/薪金.png',dpi = 1500)
from scipy.stats import zscore
from numpy import where,abs,median,nan,sqrt
data["Salary"] = data["Salary"].replace([data["Salary"][(abs(zscore(data["Salary"])) > 3)]], median(data["Salary"]))
font2 = {'family' : 'Times New Roman',
'weight' : 'normal',
'size' : 23,}
plot = sns.displot(data=data["Salary"], kde=True)
plt.title('正态分布薪金', fontsize=23)
plt.ylabel('Salary',font2)
plt.xlabel('Count',font2)
plt.savefig('C:/Users/LENOVO/Desktop/正态分布薪金.jpg',dpi = 1500)
data.describe(include='all')
data.replace(to_replace=-1, value=0,inplace=True)
将数据当中的所有-1都变成0。因为 -1 表示学生没有选这门课,为了方便起见将-1换成0,表示此模块对薪水没有任何贡献。
皮尔逊相关系数相关系数热力图:
import seaborn as sns
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.figure(figsize=(16, 16))
plt.title('特征间的皮尔森相关系数', fontsize=20)
fig = sns.heatmap(data.corr(), annot=True, cmap='rainbow')
heatmap = fig.get_figure()
heatmap.savefig('C:/Users/LENOVO/Desktop/特征间的皮尔森相关系数.jpg',dpi=2000, bbox_inches="tight")
将ID和DOB列删除,因为这两列和薪水的关系明显不大。
data_drop = data.drop(columns=["ID", "DOB"], inplace=False)
计算方差膨胀因子:(但是会报错啊,咋搞)
from statsmodels.stats.outliers_influence import variance_inflation_factor
X = data_drop[['Gender', '10percentage', '12graduation', '12percentage', 'CollegeID', 'CollegeTier', 'collegeGPA', 'CollegeCityID', 'CollegeCityTier', 'GraduationYear', 'English', 'Logical', 'Quant', 'Domain', 'ComputerProgramming', 'ElectronicsAndSemicon', 'ComputerScience', 'MechanicalEngg', 'ElectricalEngg', 'TelecomEngg', 'CivilEngg', 'conscientiousness', 'agreeableness', 'extraversion', 'nueroticism', 'openess_to_experience', 'Salary']]
vif_data = pd.DataFrame()
vif_data["Column"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
vif_data
font2 = {'family' : 'Times New Roman',
'weight' : 'normal',
'size' : 23,}
fig, [ax1,ax2] = plt.subplots(1, 2, figsize=(12, 6))
sns.countplot(x = 'Gender', data = data_drop, ax=ax1)
ax1.set_ylabel('Count',font2) #为子图设置横轴标题
ax1.set_xlabel('Gender',font2) #为子图设置纵轴标题
sns.violinplot(x = 'Gender',y = 'Salary', data = data_drop, ax=ax2, fontsize=23)
ax1.set_title('Gender数量统计', fontsize=23)
ax2.set_title('Gender与Salary统计图', fontsize=23)
ax2.set_ylabel('Salary',font2)
ax2.set_xlabel('Gender',font2)
plt.savefig('C:/Users/LENOVO/Desktop/Gender.jpg',dpi=2000, bbox_inches="tight")

我将性别映射到整数,以便可以在计算中使用。0代表男性,1代表女性。
data_drop["Gender"] = data_drop["Gender"].replace({'m': 0, 'f': 1})
plt.figure(figsize = (7,7))
explod=(0.3,0.3,0.3,0.3)
# wedgeprops='dict(width=0.1)','dict(width=0.1)','dict(width=0.1)','dict(width=0.1)'
colors='#A7D67F','#FFCC80','#94C6DC','#E2A389'
data['Degree'].value_counts().plot(
kind = 'pie', #选择图形类型
autopct = '%.2f%%', #饼图中添加数值标签
explode=explod,
radius = 1, #设置饼图半径
colors=colors,
startangle = 180, #设置饼图的初始角度
counterclock = False, #将饼图的顺序设置为顺时针方向
title = 'Degree分布', #为饼图添加标题
# shadow=True,
textprops = {'fontsize':14, 'color':'black'}, #设置文本标签的属性值)
plt.savefig('C:/Users/LENOVO/Desktop/Degree分布.jpg',dpi=2000, bbox_inches="tight")
sns.catplot(x = 'Degree', y ='Salary', hue="Degree", data = data)
plt.title('Degree与Salary分布')
plt.savefig('C:/Users/LENOVO/Desktop/Degree与Salary分布.jpg',dpi=2000, bbox_inches="tight")
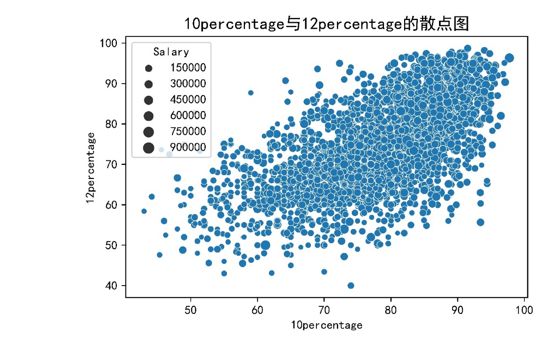
plot = sns.scatterplot(x=data['10percentage'], y=data['12percentage'], size=data['Salary'])
plot.set_title("10percentage与12percentage的散点图", fontsize=14)
plt.savefig('C:/Users/LENOVO/Desktop/10percentage与12percentage的散点图.jpg',dpi=2000, bbox_inches="tight")
data_drop["10percentage"].corr(data_drop["12percentage"])
data_drop2 = data_drop.drop(columns=["10percentage"])
将10%删除。
plot = sns.scatterplot(x=data['CollegeID'], y=data['CollegeCityID'], size=data['Salary'])
plot.set_title("CollegeID与CollegeCityID的散点图", fontsize=14)
plt.savefig('C:/Users/LENOVO/Desktop/CollegeID与CollegeCityID的散点图.jpg',dpi=2000, bbox_inches="tight")
data_drop3 = data_drop2.drop(columns=["CollegeID"])
data_drop3["CollegeCityID"].nunique()
plot = sns.scatterplot(x=data['12graduation'], y=data['GraduationYear'], size=data['Salary'])
plot.set_title("12graduation与GraduationYear的散点图", fontsize=14)
plt.savefig('C:/Users/LENOVO/Desktop/12graduation与GraduationYear的散点图.jpg',dpi=2000, bbox_inches="tight")
data_drop3 = data_drop3[data_drop3["GraduationYear"]> 1750]
data_drop3["GraduationYear"].corr(data_drop3["12graduation"])
data_drop4.drop(columns=["10board"])
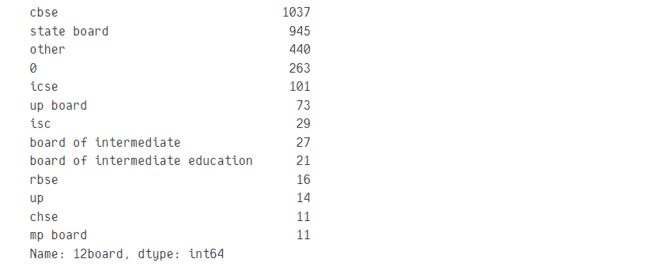
board = data_drop4["12board"].value_counts()
rare_board = board[board <= 10]
def remove_rare_board(value):
if value in rare_board:
return 'other'
else:
return value
data_drop4["12board"] = data_drop4["12board"].apply(remove_rare_board)
data_drop4["12board"].value_counts()
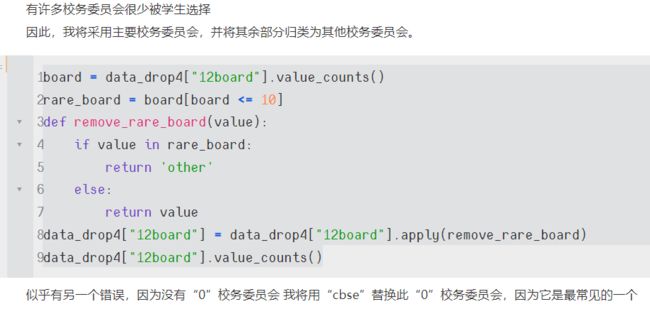
data_drop4["12board"].replace(to_replace='0',value='cbse', inplace=True)
df = pd.get_dummies(data_drop4, columns=["12board"], prefix="board_")
# prefix="board_":是自定义的前缀
df = pd.get_dummies(df, columns=["Degree"], prefix="degree_")
![]()
plt.figure(figsize = (10,15))
sns.countplot(y = 'Specialization',data = data)
plt.savefig('C:/Users/LENOVO/Desktop/Specialization数量统计.jpg',dpi=2000, bbox_inches="tight")
定义函数,将Specialization属性当中是小于10个的类别归为其他类:
specializations = df["Specialization"].value_counts()
rare_specialization = specializations[specializations <= 10]
def remove_rare_specializations(value):
if value in rare_specialization:
return 'other'
else:
return value
df["Specialization"] = df["Specialization"].apply(remove_rare_specializations)
df["Specialization"].value_counts()
# 转换为数字
df = pd.get_dummies(df, columns=["Specialization"], prefix="specialization_")
plot = sns.scatterplot(x=df["CollegeTier"], y=df["CollegeCityTier"])
plot.set_title("Scatter Plot of CollegeTier with CollegeCityTier", fontsize=14)
plt.savefig('C:/Users/LENOVO/Desktop/CollegeTier和CollegeCityTier的散点图.jpg',dpi=2000, bbox_inches="tight")
删除CollegeCityTier,因为它不像CollegeTier那样相关:
df.drop(columns=["CollegeCityTier"], inplace=True)
将GraduationYear进行归一化:
df = pd.get_dummies(df, columns=["CollegeState"], prefix="state_")
df = pd.get_dummies(df, columns=["CollegeTier"], prefix="tier_")
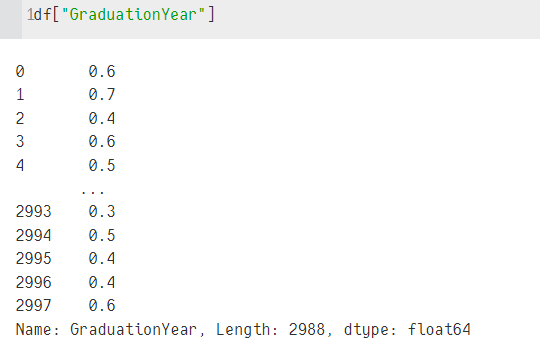
df["GraduationYear"] = (df["GraduationYear"] - df["GraduationYear"].min())/(df["GraduationYear"].max() - df["GraduationYear"].min())
df.columns
'''
Index(['Gender', '10board', '12percentage', 'collegeGPA', 'CollegeCityID',
'GraduationYear', 'English', 'Logical', 'Quant', 'Domain',
'ComputerProgramming', 'ElectronicsAndSemicon', 'ComputerScience',
'MechanicalEngg', 'ElectricalEngg', 'TelecomEngg', 'CivilEngg',
'conscientiousness', 'agreeableness', 'extraversion', 'nueroticism',
'openess_to_experience', 'Salary', 'board__board of intermediate',
'board__board of intermediate education', 'board__cbse', 'board__chse',
'board__icse', 'board__isc', 'board__mp board', 'board__other',
'board__rbse', 'board__state board', 'board__up', 'board__up board',
'degree__B.Tech/B.E.', 'degree__M.Sc. (Tech.)', 'degree__M.Tech./M.E.',
'degree__MCA', 'specialization__biotechnology',
'specialization__civil engineering',
'specialization__computer application',
'specialization__computer engineering',
'specialization__computer science & engineering',
'specialization__electrical engineering',
'specialization__electronics & instrumentation eng',
'specialization__electronics & telecommunications',
'specialization__electronics and communication engineering',
'specialization__electronics and electrical engineering',
'specialization__electronics and instrumentation engineering',
'specialization__electronics engineering',
'specialization__information science engineering',
'specialization__information technology',
'specialization__instrumentation and control engineering',
'specialization__mechanical engineering', 'specialization__other',
'state__Andhra Pradesh', 'state__Assam', 'state__Bihar',
'state__Chhattisgarh', 'state__Delhi', 'state__Goa', 'state__Gujarat',
'state__Haryana', 'state__Himachal Pradesh', 'state__Jammu and Kashmir',
'state__Jharkhand', 'state__Karnataka', 'state__Kerala',
'state__Madhya Pradesh', 'state__Maharashtra', 'state__Meghalaya',
'state__Orissa', 'state__Punjab', 'state__Rajasthan', 'state__Sikkim',
'state__Tamil Nadu', 'state__Telangana', 'state__Union Territory',
'state__Uttar Pradesh', 'state__Uttarakhand', 'state__West Bengal',
'tier__1', 'tier__2'],
dtype='object')
'''
2、模型建立
from pandas import DataFrame, read_csv, get_dummies
import pandas as pd
from scipy.stats import zscore
from statsmodels.stats.outliers_influence import variance_inflation_factor
from matplotlib.pyplot import figure, subplot2grid
from seaborn import set_theme,scatterplot,displot,barplot,countplot,heatmap
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score,mean_squared_error
from numpy import where,abs,median,nan,sqrt
import numpy as np
%matplotlib inline
set_theme(context="notebook",style='darkgrid', palette='inferno')
df = read_csv('./After.csv')
【1】岭回归
因为存在一些多重共线性,在这种情况下,岭回归提供了优势
from sklearn import metrics
data = df.copy()
X = data.drop(columns=["Salary"])
y = data[["Salary"]]
X_train,X_test,y_train,y_test = train_test_split(X,y, test_size=0.4,random_state=49, shuffle=True)
model = Ridge(alpha=10)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
print(sqrt(mean_squared_error(y_test,y_pred)))
print(r2_score(y_test,y_pred))
print(model.coef_) # 回归系数
print(model.get_params()) # 输出参数设置
import matplotlib.pyplot as plt
plt.figure(num=3, figsize=(30, 12))
plt.plot(range(len(y_pred)), y_pred, 'b', label="predict")
plt.plot(range(len(y_test)), y_test, 'r', label="predict")
plt.savefig('C:/Users/LENOVO/Desktop/拟合曲线.jpg',dpi=1000, bbox_inches="tight")
【2】随机森林
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(n_estimators=10000, random_state=0, n_jobs=-1)
forest.fit(X_train, y_train)
importances = forest.feature_importances_
importances
y2 = pd.DataFrame(importances)
y2.to_excel('C:/Users/LENOVO/Desktop/importances.xlsx', header=True, index=None)
【3】多元线性回归
import pandas as pd
import statsmodels.api as sm
x_ = sm.add_constant(X)
Lin = sm.OLS(y, x_)
coal = Lin.fit()
print(coal.summary())
print(coal.params)
Y_pred = coal.predict(x_)
import matplotlib.pyplot as plt
plt.figure(num=3, figsize=(30, 12))
plt.plot(range(len(Y_pred)), Y_pred, 'g', label="predict")
plt.plot(range(len(y)), y, 'r', label="true")
plt.savefig('C:/Users/LENOVO/Desktop/拟合曲线.jpg',dpi=1000, bbox_inches="tight")
y1 = pd.DataFrame(coal.params)
y1.to_excel('C:/Users/LENOVO/Desktop/多元线性回归coal.xlsx', header=True, index=None)
output = pd.DataFrame(data=df)
output.to_csv('C:/Users/LENOVO/Desktop/After.csv', header=True, index=None)
3、影响Salary的因素
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_style('darkgrid')
%matplotlib inline
data = pd.read_csv('./B题附件.csv')
data.corr(method="pearson").to_csv('皮尔逊相关系数.csv')
data = data.drop(['ID','CollegeCityID','CollegeID','DOB'], axis =1)
data = data.drop(data[data['Degree'] == 'M.Sc. (Tech.)'].index, axis =0)
data['CollegeCityTier'] = data['CollegeCityTier'].astype('object')
data['CollegeTier'] = data['CollegeTier'].astype('object')
data.select_dtypes('number').columns[:-1]
plt.figure(figsize = (17,5))
plt.subplot(1,2,1)
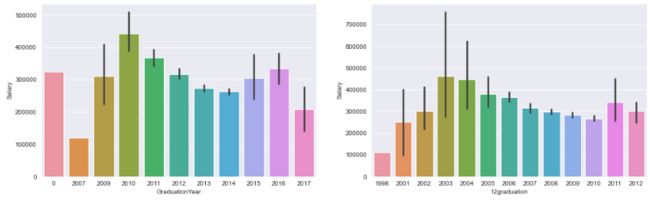
sns.barplot(data = data , x = 'GraduationYear',y = 'Salary')
plt.subplot(1,2,2)
sns.barplot(data = data , x = '12graduation',y = 'Salary')
plt.savefig('C:/Users/LENOVO/Desktop/12graduation和GraduationYear与Salary的关系.jpg',dpi = 1000)
plt.figure(figsize = (10,15))
sns.boxplot(y = 'Specialization',x = 'Salary',data = data
,flierprops = {'marker':'o',#异常值形状
'markerfacecolor':'red',#形状填充色
'color':'black',#形状外廓颜色
}
,medianprops = {'linestyle':'--','color':'red'})
plt.savefig('C:/Users/LENOVO/Desktop/Specialization与Salary的关系.jpg',dpi = 1500)
plt.figure(figsize = (25,25))
for i,col in enumerate(data.select_dtypes('number').columns[:-1]):
plt.subplot(7,3,i+1)
sns.scatterplot(x = col, y = 'Salary', data = data)
plt.savefig('C:/Users/LENOVO/Desktop/多种因素与Salary的关系.jpg',dpi = 1000)
plt.show()