一文带你了解科学计算库 numpy

---

前言

Numpy（Numerical Python）是一个开源的Python科学计算库，用于快速处理任意维度的数组。

Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务，使用Numpy比直接使用Python要简洁的多。

Numpy使用ndarray对象来处理多维数组，该对象是一个快速而灵活的大数据容器。

NumPy提供了一个N维数组类型ndarray，它描述了相同类型的“items”的集合。

机器学习的最大特点就是大量的数据运算，那么如果没有一个快速的解决方案，那可能现在python也在机器学习领域达不到好的效果。

Numpy底层使用C语言编写，内部解除了GIL（全局解释器锁），其对数组的操作速度不受Python解释器的限制，所以，其效率远高于纯Python代码。

numpy内置了并行运算功能，当系统有多个核心时，做某种计算时，numpy会自动做并行计算.

引入库

import numpy as np

import warnings
warnings.filterwarnings('ignore')

初始数组

类比Excel表格，一维数组就相当于一行，二位数组就相当于一个表格，三维数组就是一个工作簿中的多个表，以此类推，我们常用的是一维数组、二维数组，三维数组用的比较少

• 一维数组

arr = np.array([1,2,3,4])
arr

结果：

• 二维数组

score = np.array(
[[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]]
)

结果：

属性

1. 形状

score.shape

# 结果
(8, 5)
# 可以理解为8行5列的表

2. 维度

score.ndim
# 结果
2
# 表示这个矩阵是二维的

3. 元素个数

score.size
# 结果
40
# 一共有40个元素

4. 类型

score.dtype
# 结果
dtype('int32')
# 元素属性是 int32 类型的

创建数组及基本操作

• 生成数组

1. 全是0的数组

np.zeros(shape=(10,5),dtype=np.int64)

**结果： **

2. 全是1的数组

np.ones(shape=(10,5),dtype=np.int64)

结果：

3. 现有数组生成

a = np.array([[1,2,3],[2,3,4]])
np.asarray(a,dtype='uint32')

结果：

• 生成特殊数组

1. 等间距数列

np.linspace(
    start,
    stop,
    num=50,
    endpoint=True,
    retstep=False,
    dtype=None,
    axis=0,
)
# start:序列的起始值
# stop:序列的终止值
# num:要生成的等间隔样例数量，默认为50
# endpoint:序列中是否包含stop值，默认为ture

np.linspace(0, 100, 11,dtype=np.int32)
# 结果
array([  0,  10,  20,  30,  40,  50,  60,  70,  80,  90, 100])

2. 等差数列

np.arange(1,10,2)
# 结果
array([1, 3, 5, 7, 9])

3. 10^n等比数组

np.logspace(start=1,stop=3, num=3)
# 结果

array([  10.,  100., 1000.])

• 生成随机数组

1. 正态分布

标准正太分布

np.random.randn(10)

结果：

指定的正态分布

np.random.normal(loc=1, scale=1.0, size=(5,5))

结果：

方法参数详解

np.random.normal(
    loc,    # 正态分布的中心
    scale,   # 分布的宽度(标准差)
    size    # shape(形状)
)

指定shape的标准正态分布

np.random.standard_normal(size=(5,5))   

结果：

2. 均匀分布

[0,1]之间的均匀分布

np.random.rand(3,3)   # 数组，传几个参数就是几维数组

结果：

指定区间的均匀分布数组

np.random.uniform(low=0.0, high=1.0, size=None)
# 结果
0.788561235247165

# 参数
# low: 采样下界，float类型，默认值为0；
# high: 采样上界，float类型，默认值为1；
# size: 输出样本数目，为int或元组(tuple)类型，例如，size=(m,n,k), 则输出mnk个样本，缺省时输出1个值。

指定范围的整数型均匀分布

从一个均匀分布中随机采样，生成一个整数或N维整数数组

np.random.randint(
    low=1,        # 最小值 
    high=10,       # 最大值
    size=(10,10),    # shape
    dtype='l'
)

• 数组的索引、切片

数组的切片可以类比列表的切片，但是数组的切片涉及到维度，略有不同

arr = np.random.randint(1,10,(3,3))

数组的切片是先行后列

arr[0,:3]    # ：3 左闭右开区间，即含左不含右
# 0 行 前三个元素
# 结果
array([2, 3, 4])

• 修改形状

修改形状必须保持修改前后元素的个数必须一致

arr.reshape((9,1))

**结果： **

arr.resize((1,9))

结果：

reshape 和 resize 的区别在于，reshape不改变原有数组返回新的数组，resize直接改变原数组

• 数组转置

数组的行列转换

arr.T

**结果： **

• 类型转换

arr.dtype
# 结果
dtype('int32')

arr.astype('int64')

结果：

• 数组转Python列表

arr.tolist()

# 结果
[[2, 3, 4, 6, 3, 6, 8, 6, 3]]

• 多维数组转列表

arr.flatten().tolist()  # 压缩成一维数组再转换
# 结果
[2, 3, 4, 6, 3, 6, 8, 6, 3]

• 数组去重

temp = np.array([[1, 2, 3, 4],[3, 4, 5, 6]])
np.unique(temp)
# 结果
array([1, 2, 3, 4, 5, 6])

数组的计算

• 逻辑运算

score = np.random.randint(40, 100, (10, 5))

score>60

结果：

逻辑运算有 >,<,==,>=,<=,!=等等

筛选大于60的值

score[score>60]

结果：

• 通用判断

1. all

np.all(score)
# 结果

True

数组中是否全部为True，python中，不等于0都代表True，等个0代表False

2. any

np.any(score)
# 结果
True

数组中是否至少一个为True

• 三元运算

python有三元运算，numpy中也有，但是会有所不同

a = 77
print('及格' if a>=60 else "不及格" )

# 结果
'及格'

python的三元运算嵌套

a = 77
print('A' if a>=90 else "B" if a>=75 and a<90 else "C" if a>=60 and a<75 else "D")

# 结果
B

numpy的三元运算

score

np.where(score>60,'合格','不合格')

结果：

numpy三元运算嵌套

np.where(score>=90,"A",
         np.where(np.logical_and(score>=75,score<90),"B",
         np.where(np.logical_and(score>=60,score<75),"C","D")))

**结果： **

numpy中逻辑and 和 or，不能直接使用，需要用到特定的函数 np.logical_and和np.logical_or

• 描述性统计指标

1. 和

score.sum()
# 结果
3507

score.sum(axis=1)  # axis=None求全部的，axis=0,按列统计，axis=1按行统计

# 结果
array([287, 421, 323, 366, 360, 301, 401, 305, 381, 362])

2. 最大值

score.max()
# 结果
98

3. 平均值

ndarray的最大、最小、平均值、和等方法底层是调用了numpy的相关方法，他们的计算结果一样

score.mean()
# 结果  70.14
np.mean(score)
# 结果  70.14

4. 中位数

ndarray没有中位数的方法，可以调用numpy的中位数方法

np.median(score)
# 结果
72.5

• 方差、 标准差

score.var(),score.std()
# 结果
(300.8404, 17.344751367488666)

• 数组间的运算

1.数组与数的运算

数组与数的运算，其实就是数组中的每个元素与这个数的运算

score*10

**结果： **

score // 10

2. 数组与数组间的运算

数组间的基本运算必须是两个相同结构的数组，即行列必须一致

score_1 = np.ones_like(score)
score_1

结果

两个数组间的基本运算 就是对应位置的元素的基本运算

score+score_1

结果

3. 数组相乘

score / (score_1 * 2)

结果：

广播机制

广播机制实现了时两个或两个以上数组的运算，即使这些数组的shape不是完全相同的，只需要满足如下任意一个条件即可。

1.数组的某一维度等长。

2.其中一个数组的某一维度为1 。

广播机制需要扩展维度小的数组，使得它与维度最大的数组的shape值相同，以便使用元素级函数或者运算符进行运算。

arr_a = np.random.randint(10,100,(10,5))
arr_a

arr_b = np.random.randint(10,100,5)
arr_b

**结果： **

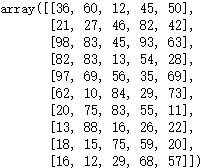
arr_a + arr_b

结果

广播机制要求在某个维度上的长度一致，另一个维度为1，numpy会将为1的维度扩展成与运算对象一样的维度

• 矩阵

矩阵必须是二维的，向量是特殊的矩阵，一列就是一个向量

相同行列数的矩阵之间的基本运算与数组一样，矩阵间的乘法称为点乘

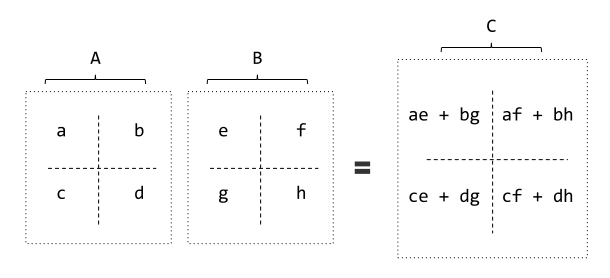
点乘的运算原理

A矩阵的第 m 行 与 B矩阵的m列元素一一相乘并求和，得到结果的一个元素

以一个二维矩阵为例，其结果是这样来的

矩阵间的点乘必须遵循

–(M行, N列)*(N行, L列) = (M行, L列)–

met_1 = np.random.randint(10,50,(10,2))
met_2 = np.random.randint(10,50,(2,5))
np.dot(met_1,met_2)

**结果： **

np.matmul 与 np.dot 都是求矩阵的点乘， 区别在于matmul 不支持矩阵与标量间的运算

总结

代码的功底都是通过不断的练习一步步积累起来的，和我一起学pandas吧！