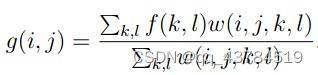OpenCV数字图像处理基于C++：图像平滑
OpenCV数字图像处理基于C++：图像平滑
1、图像平滑算法
图像平滑是一种区域增强的算法，平滑算法有邻域平均法、空间低通滤波、多图像平均、中值滤波等。在图像产生、传输和复制过程中，常常会因为多方面原因而被噪声干扰或出现数据丢失，降低了图像的质量（某一像素，如果它与周围像素点相比有明显的不同，则该点被噪声所感染）。这就需要对图像进行一定的增强处理以减小这些缺陷带来的影响。
图像平滑从信号处理的角度看就是去除其中的高频信息，保留低频信息。因此我们可以对图像实施低通滤波。低通滤波可以去除图像中的噪音，模糊图像(噪音是图像中变化比较大的区域，也就是高频信息)。而高通滤波能够提取图像的边缘(边缘也是高频信息集中的区域)。
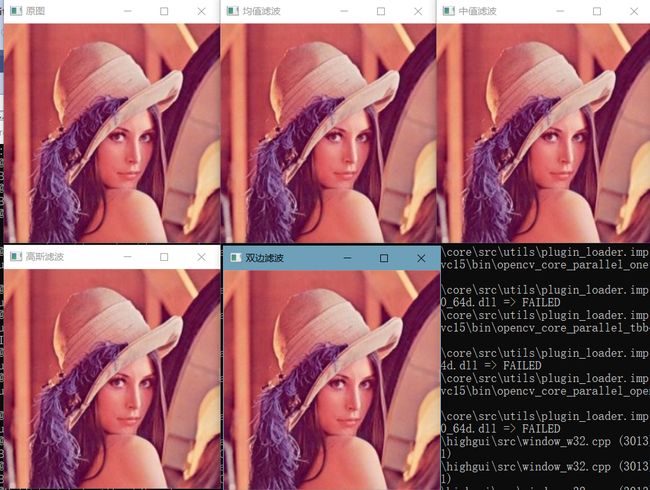
根据滤波器的不同又可以分为均值滤波，高斯加权滤波，中值滤波， 双边滤波。
图像滤波的目的有两个:
一是抽出对象的特征作为图像识别的特征模式;
二是为适应图像处理的要求，消除图像数字化时所混入的噪声。
对滤波处理的要求也有两条:
一是不能损坏图像的轮廓及边缘等重要信息;
二是使图像清晰视觉效果好。
平滑滤波是低频增强的空间域滤波技术。它的目的有两类：
一类是模糊；另一类是消除噪音。
空间域的平滑滤波一般采用简单平均法进行，就是求邻近像元点的平均亮度值。邻域的大小与平滑的效果直接相关，邻域越大平滑的效果越好，但邻域过大，平滑会使边缘信息损失的越大，从而使输出的图像变得模糊，因此需合理选择邻域的大小。
关于滤波器，一种形象的比喻法是：我们可以把滤波器想象成一个包含加权系数的窗口，当使用这个滤波器平滑处理图像时，就把这个窗口放到图像之上，透过这个窗口来看我们得到的图像。
2、线性滤波
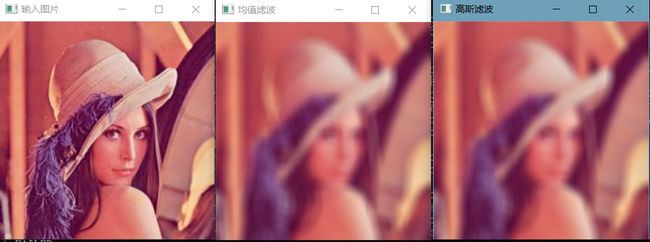
2.1 均值滤波
一个方块区域（一般为3*3）内，中心点的像素为全部点像素值的平均值。均值滤波就是对于整张图片进行以上操作。均值滤波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，不能很好地去除噪声点。特别是校验噪声。（均值滤波是方波滤波归一化后的特殊情况）
2.2 实现均值滤波
非官方编写的均值滤波
//均值滤波
void AverFiltering(const Mat& src, Mat& dst) {
if (!src.data) return;
//at访问像素点
for (int i = 1; i < src.rows; ++i)
for (int j = 1; j < src.cols; ++j) {
if ((i - 1 >= 0) && (j - 1) >= 0 && (i + 1) < src.rows && (j + 1) < src.cols) {//边缘不进行处理
dst.at(i, j)[0] = (src.at(i, j)[0] + src.at(i - 1, j - 1)[0] + src.at(i - 1, j)[0] + src.at(i, j - 1)[0] +
src.at(i - 1, j + 1)[0] + src.at(i + 1, j - 1)[0] + src.at(i + 1, j + 1)[0] + src.at(i, j + 1)[0] +
src.at(i + 1, j)[0]) / 9;
dst.at(i, j)[1] = (src.at(i, j)[1] + src.at(i - 1, j - 1)[1] + src.at(i - 1, j)[1] + src.at(i, j - 1)[1] +
src.at(i - 1, j + 1)[1] + src.at(i + 1, j - 1)[1] + src.at(i + 1, j + 1)[1] + src.at(i, j + 1)[1] +
src.at(i + 1, j)[1]) / 9;
dst.at(i, j)[2] = (src.at(i, j)[2] + src.at(i - 1, j - 1)[2] + src.at(i - 1, j)[2] + src.at(i, j - 1)[2] +
src.at(i - 1, j + 1)[2] + src.at(i + 1, j - 1)[2] + src.at(i + 1, j + 1)[2] + src.at(i, j + 1)[2] +
src.at(i + 1, j)[2]) / 9;
}
else {//边缘赋值
dst.at(i, j)[0] = src.at(i, j)[0];
dst.at(i, j)[1] = src.at(i, j)[1];
dst.at(i, j)[2] = src.at(i, j)[2];
}
}
}
//均值滤波
void AverFiltering(const Mat& src, Mat& dst) {
if (!src.data) return;
//at访问像素点
for (int i = 1; i < src.rows; ++i)
for (int j = 1; j < src.cols; ++j) {
if ((i - 1 >= 0) && (j - 1) >= 0 && (i + 1) < src.rows && (j + 1) < src.cols) {//边缘不进行处理
dst.at(i, j)[0] = (src.at(i, j)[0] + src.at(i - 1, j - 1)[0] + src.at(i - 1, j)[0] + src.at(i, j - 1)[0] +
src.at(i - 1, j + 1)[0] + src.at(i + 1, j - 1)[0] + src.at(i + 1, j + 1)[0] + src.at(i, j + 1)[0] +
src.at(i + 1, j)[0]) / 9;
dst.at(i, j)[1] = (src.at(i, j)[1] + src.at(i - 1, j - 1)[1] + src.at(i - 1, j)[1] + src.at(i, j - 1)[1] +
src.at(i - 1, j + 1)[1] + src.at(i + 1, j - 1)[1] + src.at(i + 1, j + 1)[1] + src.at(i, j + 1)[1] +
src.at(i + 1, j)[1]) / 9;
dst.at(i, j)[2] = (src.at(i, j)[2] + src.at(i - 1, j - 1)[2] + src.at(i - 1, j)[2] + src.at(i, j - 1)[2] +
src.at(i - 1, j + 1)[2] + src.at(i + 1, j - 1)[2] + src.at(i + 1, j + 1)[2] + src.at(i, j + 1)[2] +
src.at(i + 1, j)[2]) / 9;
}
else {//边缘赋值
dst.at(i, j)[0] = src.at(i, j)[0];
dst.at(i, j)[1] = src.at(i, j)[1];
dst.at(i, j)[2] = src.at(i, j)[2];
}
}
}
//图像椒盐化
void salt(Mat& image, int num) {
if (!image.data) return;//防止传入空图
int i, j;
srand(time(NULL));
for (int x = 0; x < num; ++x) {
i = rand() % image.rows;
j = rand() % image.cols;
if (image.channels() == 1)
{
image.at(i, j) = 255;
}
else if (image.channels() == 3)
{
image.at(i, j)[0] = 255;
image.at(i, j)[1] = 255;
image.at(i, j)[2] = 255;
}
}
}
void main() {
Mat image = imread("E:\\Lena.jpg");
Mat Salt_Image;
image.copyTo(Salt_Image);
salt(Salt_Image, 3000); //添加噪声
Mat image1(image.size(), image.type()); //创建一个跟原图大小相等的图片
Mat image2;
AverFiltering(Salt_Image, image1);
blur(Salt_Image, image2, Size(3, 3));//openCV库自带的均值滤波函数
imshow("原图", image);
imshow("自定义均值滤波", image1);
imshow("openCV自带的均值滤波", image2);
waitKey();
}
//定义全局变量
Mat g_srcImage; //定义输入图像
Mat g_dstImage; //定义目标图像
const int g_nTrackbarMaxValue = 9; //定义轨迹条最大值
int g_nTrackbarValue; //定义轨迹条初始值
int g_nKernelValue; //定义kernel尺寸
void on_kernelTrackbar(int, void*); //定义回调函数
int main()
{
g_srcImage = imread("E:\\Lena.jpg");
//判断图像是否加载成功
if (g_srcImage.empty())
{
cout << "图像加载失败!" << endl;
return -1;
}
else
cout << "图像加载成功!" << endl << endl;
namedWindow("原图像", WINDOW_AUTOSIZE); //定义窗口显示属性
imshow("原图像", g_srcImage);
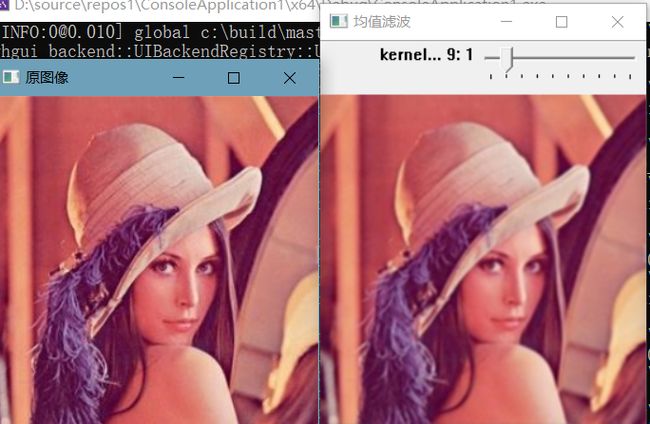
g_nTrackbarValue = 1;
namedWindow("均值滤波", WINDOW_AUTOSIZE); //定义滤波后图像显示窗口属性
//定义轨迹条名称和最大值
char kernelName[20];
sprintf_s(kernelName, "kernel尺寸 %d", g_nTrackbarMaxValue);
//创建轨迹条
createTrackbar(kernelName, "均值滤波", &g_nTrackbarValue, g_nTrackbarMaxValue, on_kernelTrackbar);
on_kernelTrackbar(g_nTrackbarValue, 0);
waitKey(0);
return 0;
}
void on_kernelTrackbar(int, void*)
{
//根据输入值重新计算kernel尺寸
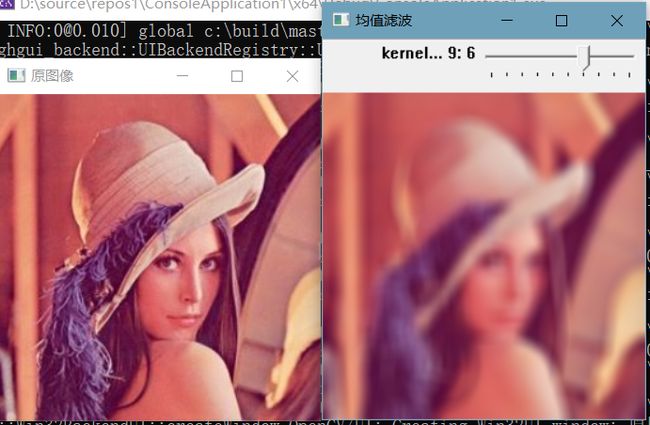
g_nKernelValue = g_nTrackbarValue * 2 + 1;
//均值滤波函数
blur(g_srcImage, g_dstImage, Size(g_nKernelValue, g_nKernelValue));
imshow("均值滤波", g_dstImage);
}
createTrackbar(
const string& trackbarname,
const string& winname,
int* value,
int count,
TrackbarCallback onChange = 0,
void* userdata = 0
);
其各个参数含义如下：
const string& trackname: 滑动条名字
const string& winname: 想要把该滑动条依附到的窗口名字，在程序中可能该窗口名称由namedWindow()声明。
int* value: 创建滑动条时，滑动条的初始值
int count: 滑动条的最大值，即所有滑动条的数据变动都要在0-count之间，滑动条最小值为0
TrackbarCallback onChange = 0: 这是指的回调函数，每次滑动条数据变化时都对该函数进行回调
void* userdata = 0: 这个是用户传给回调函数的数据，用来处理滑动条数值变动。如果在创建滑动条时，输入value实参是全局变量，则本参数userdata可使用默认值0.
2.3 高斯滤波
数值图像处理中，高斯滤波主要可以使用两种方法实现。一种是离散化窗口滑窗卷积，另一种方法是通过傅里叶变化。最常见的就是滑窗实现，只有当离散化的窗口非常大，用滑窗计算量非常搭的情况下，可能会考虑基于傅里叶变化的实现方法。所以本文将主要介绍滑窗实现的卷积。
离散化窗口划船卷积时主要利用的是高斯核，高斯核的大小为奇数，因为高斯卷积会在其覆盖区域的中心输出结果。常用的高斯模板有如下几种形式：
高斯模板是通过高斯函数计算出来的（正态分布），公式如下：
二维高斯函数可以表示如下：
为均值（峰值对应的位置），
为标准差（变量x和变量y各有一个均值，也各有一个标准差)。
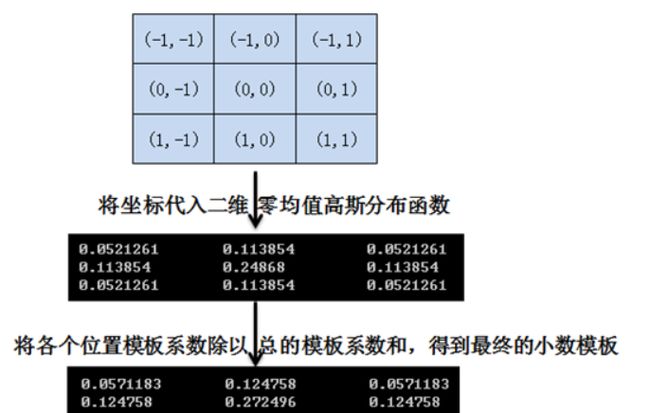
高斯滤波一般使用的二维零均值的高斯分布函数，通过高斯分布函数求出模板系数，例如一个3*3的模板：以模板的中心位置为坐标原点进行取样，其中模板各个坐标位置如下图，x轴水平向右，y轴垂直向下，（x,y）表示：
将各个位置的坐标代入二维零均值高斯分布函数，计算出来的模板有两种形式：
整数模板和小数模板，可以使用二维数组来存放计算出的模板系数。
（1）小数模板
（2）整数模板
结论:整数模板与图像进行卷积后还要除以总的模板系数和
输入：目标核，核的大小，sigma值
1.以x，y方向联合实现获取高斯模板
①取样获得模板
②将坐标代入高斯公式
③将对应的值写入高斯核中
④归一化
输入：原图像，目标图像，核
1.判断原图像是否为空，空则直接返回
2.判断核的是否为奇数
3.原图像边界填充，目标图像清空
4.用高斯核高斯滤波
2.4 实现高斯滤波
/* 高斯滤波 (待处理单通道图片, 高斯分布数组， 高斯数组大小(核大小) ) */
void gaussian(Mat* _src, double** _array, int _size)
{
Mat temp = (*_src).clone();
// [1] 扫描
for (int i = 0; i < (*_src).rows; i++) {
for (int j = 0; j < (*_src).cols; j++) {
// [2] 忽略边缘
if (i > (_size / 2) - 1 && j > (_size / 2) - 1 &&
i < (*_src).rows - (_size / 2) && j < (*_src).cols - (_size / 2)) {
// [3] 找到图像输入点f(i,j),以输入点为中心与核中心对齐
// 核心为中心参考点 卷积算子=>高斯矩阵180度转向计算
// x y 代表卷积核的权值坐标 i j 代表图像输入点坐标
// 卷积算子 (f*g)(i,j) = f(i-k,j-l)g(k,l) f代表图像输入 g代表核
// 带入核参考点 (f*g)(i,j) = f(i-(k-ai), j-(l-aj))g(k,l) ai,aj 核参考点
// 加权求和 注意：核的坐标以左上0,0起点
double sum = 0.0;
for (int k = 0; k < _size; k++) {
for (int l = 0; l < _size; l++) {
sum += (*_src).ptr(i - k + (_size / 2))[j - l + (_size / 2)] * _array[k][l];
}
}
// 放入中间结果,计算所得的值与没有计算的值不能混用
temp.ptr(i)[j] = sum;
}
}
}
// 放入原图
(*_src) = temp.clone();
}
/* 获取高斯分布数组 (核大小， sigma值) */
double** getGaussianArray(int arr_size, double sigma)
{
int i, j;
// [1] 初始化权值数组
double** array = new double* [arr_size];
for (i = 0; i < arr_size; i++) {
array[i] = new double[arr_size];
}
// [2] 高斯分布计算
int center_i, center_j;
center_i = center_j = arr_size / 2;
double pi = 3.141592653589793;
double sum = 0.0f;
// [2-1] 高斯函数
for (i = 0; i < arr_size; i++) {
for (j = 0; j < arr_size; j++) {
array[i][j] =
//后面进行归一化，这部分可以不用
//0.5f *pi*(sigma*sigma) *
exp(-(1.0f) * (((i - center_i) * (i - center_i) + (j - center_j) * (j - center_j)) /
(2.0f * sigma * sigma)));
sum += array[i][j];
}
}
// [2-2] 归一化求权值
for (i = 0; i < arr_size; i++) {
for (j = 0; j < arr_size; j++) {
array[i][j] /= sum;
printf(" [%.15f] ", array[i][j]);
}
printf("\n");
}
return array;
}
void myGaussianFilter(Mat* src, Mat* dst, int n, double sigma)
{
// [1] 初始化
*dst = (*src).clone();
// [2] 彩色图片通道分离
vector channels;
split(*src, channels);
// [3] 滤波
// [3-1] 确定高斯正态矩阵
double** array = getGaussianArray(n, sigma);
// [3-2] 高斯滤波处理
for (int i = 0; i < 3; i++) {
gaussian(&channels[i], array, n);
}
// [4] 合并返回
merge(channels, *dst);
return;
}
int main(void)
{
// [1] src读入图片
Mat src = imread("E:\\Lena.jpg");
// [2] dst目标图片
Mat dst;
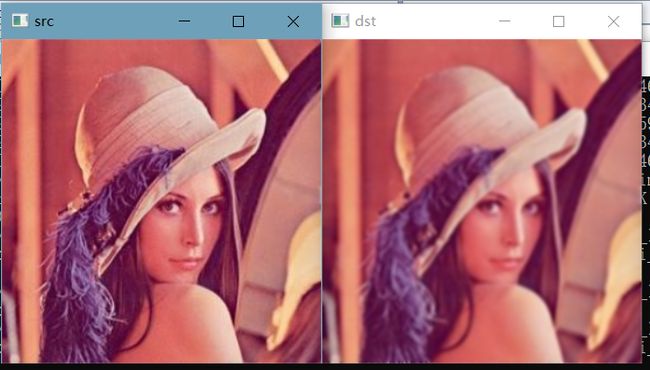
// [3] 高斯滤波 sigma越大越平越模糊
myGaussianFilter(&src, &dst, 5, 1.5f);
// [4] 窗体显示
imshow("src", src);
imshow("dst", dst);
waitKey(0);
destroyAllWindows();
return 0;
}
int main(int argc, char** argv)
{
Mat src, dst;
src = imread("E:\\Lena.jpg");
if (!src.data)
{
printf("could not load image3...\n");
return -1;
}
//定义窗口名称
char input_title[] = "输入图片";
char output_title[] = "均值滤波";
//新建窗口
namedWindow(input_title, WINDOW_AUTOSIZE);
namedWindow(output_title, WINDOW_AUTOSIZE);
imshow(input_title, src);//原图显示
//均值滤波操作
blur(src, dst, Size(15, 15), Point(-1, -1));//均值滤波，Size里面都要奇数，正数。内核内数值分别表示宽，高。Point（-1，-1）表示锚点，一般取-1，表示锚点在核中心。
imshow(output_title, dst);
Mat gblur;
//高斯滤波操作
GaussianBlur(src, gblur, Size(15, 15), 11, 11);//高斯滤波
imshow("高斯滤波", gblur);
waitKey(0);
return 0;
}
void GaussianBlur(
InputArray src,
OutputArray dst,
Size ksize,
double sigmaX,
double sigmaY=0,
int borderType=BORDER_DEFAULT
);
参数详解如下：
src，输入图像，即源图像，填Mat类的对象即可。它可以是单独的任意通道数的图片，但需要注意，图片深度应该为CV_8U,CV_16U, CV_16S, CV_32F 以及 CV_64F之一。
dst，即目标图像，需要和源图片有一样的尺寸和类型。比如可以用Mat::Clone，以源图片为模板，来初始化得到如假包换的目标图。
ksize，高斯内核的大小。其中ksize.width和ksize.height可以不同，但他们都必须为正数和奇数（并不能理解）。或者，它们可以是零的，它们都是由sigma计算而来。
sigmaX，表示高斯核函数在X方向的的标准偏差。
sigmaY，表示高斯核函数在Y方向的的标准偏差。若sigmaY为零，就将它设为sigmaX，如果sigmaX和sigmaY都是0，那么就由ksize.width和ksize.height计算出来。
3、非线性滤波
3.1 中值滤波
中值滤波会取当前像素点及其周围临近像素点（一共有奇数个像素点）的像素值，将这些像素值排序，然后将位于中间位置的像素值作为当前像素点的像素值。
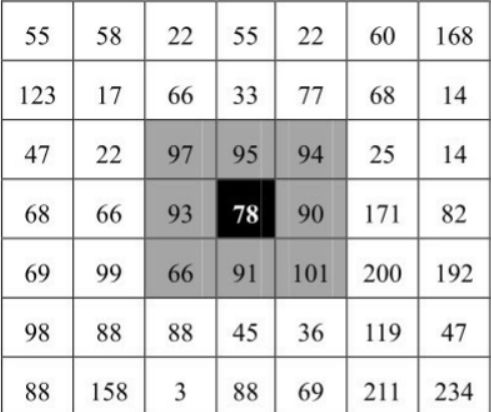
对如下矩阵：
将其邻域设置为3×3大小，对其3×3邻域内像素点的像素值进行排序（升序降序均可），按升序排序后得到序列值为：[66,78,90,91,93,94,95,97,101]。在该序列中，处于中心位置（也叫中心点或中值点）的值是“93”，因此用该值替换原来的像素值78，作为当前点的新像素值。中值滤波效果如下：
3.2 实现中值滤波
//求九个数的中值
uchar Median(uchar n1, uchar n2, uchar n3, uchar n4, uchar n5,
uchar n6, uchar n7, uchar n8, uchar n9) {
uchar arr[9];
arr[0] = n1;
arr[1] = n2;
arr[2] = n3;
arr[3] = n4;
arr[4] = n5;
arr[5] = n6;
arr[6] = n7;
arr[7] = n8;
arr[8] = n9;
for (int gap = 9 / 2; gap > 0; gap /= 2)//希尔排序
for (int i = gap; i < 9; ++i)
for (int j = i - gap; j >= 0 && arr[j] > arr[j + gap]; j -= gap)
swap(arr[j], arr[j + gap]);
return arr[4];//返回中值
}
//图像椒盐化
void salt(Mat& image, int num) {
if (!image.data) return;//防止传入空图
int i, j;
srand(time(NULL));
for (int x = 0; x < num; ++x) {
i = rand() % image.rows;
j = rand() % image.cols;
image.at(i, j)[0] = 255;
image.at(i, j)[1] = 255;
image.at(i, j)[2] = 255;
}
}
//中值滤波函数
void MedianFlitering(const Mat& src, Mat& dst) {
if (!src.data)return;
Mat _dst(src.size(), src.type());
for (int i = 0; i < src.rows; ++i)
for (int j = 0; j < src.cols; ++j) {
if ((i - 1) > 0 && (i + 1) < src.rows && (j - 1) > 0 && (j + 1) < src.cols) {
_dst.at(i, j)[0] = Median(src.at(i, j)[0], src.at(i + 1, j + 1)[0],
src.at(i + 1, j)[0], src.at(i, j + 1)[0], src.at(i + 1, j - 1)[0],
src.at(i - 1, j + 1)[0], src.at(i - 1, j)[0], src.at(i, j - 1)[0],
src.at(i - 1, j - 1)[0]);
_dst.at(i, j)[1] = Median(src.at(i, j)[1], src.at(i + 1, j + 1)[1],
src.at(i + 1, j)[1], src.at(i, j + 1)[1], src.at(i + 1, j - 1)[1],
src.at(i - 1, j + 1)[1], src.at(i - 1, j)[1], src.at(i, j - 1)[1],
src.at(i - 1, j - 1)[1]);
_dst.at(i, j)[2] = Median(src.at(i, j)[2], src.at(i + 1, j + 1)[2],
src.at(i + 1, j)[2], src.at(i, j + 1)[2], src.at(i + 1, j - 1)[2],
src.at(i - 1, j + 1)[2], src.at(i - 1, j)[2], src.at(i, j - 1)[2],
src.at(i - 1, j - 1)[2]);
}
else
_dst.at(i, j) = src.at(i, j);
}
_dst.copyTo(dst);//拷贝
}
int main() {
Mat image = imread("E:\\Lena.jpg");
imshow("原图", image);
Mat Salt_Image;
image.copyTo(Salt_Image);
salt(Salt_Image, 3000);
imshow("椒盐图", Salt_Image);
Mat image3, image4;
MedianFlitering(Salt_Image, image3);
medianBlur(Salt_Image, image4, 3);
imshow("自定义中值滤波处理后", image3);
imshow("openCV自带的中值滤波", image4);
waitKey();
return 0;
}
int main()
{
// 载入原图
Mat image = imread("E:\\Lena.jpg");
//创建窗口
namedWindow("中值滤波【原图】");
namedWindow("中值滤波【效果图】");
//显示原图
imshow("中值滤波【原图】", image);
//salt(image, 3000); //添加噪声
//显示椒盐图
//imshow("中值滤波【椒盐图】", image);
//进行中值滤波操作
Mat out;
medianBlur(image, out, 3);//输入，输出，7通道
//显示效果图
imshow("中值滤波【效果图】", out);
waitKey(0);
}
可以看出中值滤波对噪声的消除效果比线性滤波好，但是随着滤波核的增大，图像也会变模糊。
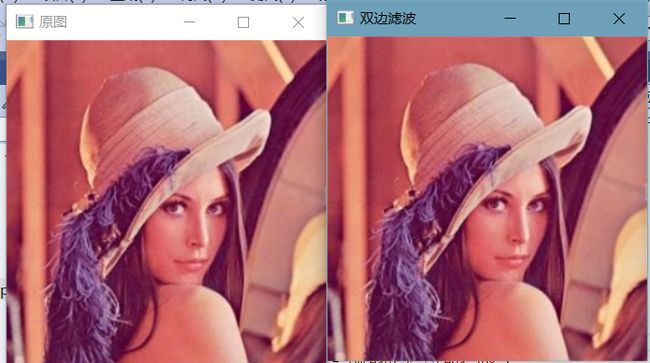
3.3 双边滤波
双边滤波是一种非线性的滤波方法，是结合图像的空间邻近度和像素值相似度的一种折衷处理，同时考虑空间与信息和灰度相似性，达到保边去噪的目的，具有简单、非迭代、局部处理的特点。之所以能够达到保边去噪的滤波效果是因为滤波器由两个函数构成：一个函数是由几何空间距离决定滤波器系数，另一个是由像素差值决定滤波器系数。
双边滤波器中，输出像素的值依赖于邻域像素的值的加权组合，其公式如下：
双边滤波器中，输出像素的值依赖于邻域像素的值的加权组合，
权重系数w(i,j,k,l)取决于定义域核
和值域核
的乘积
通俗来讲就是双边滤波模板主要有两个模板生成，第一个是高斯模板，第二个是以灰度级的差值作为函数系数生成的模板，然后这两个模板点乘就得到了最终的双边滤波模板，第一个模板是全局模板，所以只需要生成一次，第二个模板需要对每个像素都计算一次。双边滤波器比高斯滤波器多了一个高斯方差sigma-d,它是基于空间分布的高斯滤波函数，所以在边缘附近，离的较远的像素不会太多影响到边缘上的像素，这样就能对边缘附近的像素值予以保存，但是由于保存过多的高频信息，对于彩色图像里的高频噪声，双边滤波器不能够干净的滤掉，只能够对于低频信息进行较好的滤除。
//获取色彩模板（值域模板）
///
void getColorMask(std::vector& colorMask, double colorSigma) {
for (int i = 0; i < 256; ++i) {
double colordiff = exp(-(i * i) / (2 * colorSigma * colorSigma));
colorMask.push_back(colordiff);
}
}
//获取高斯模板（空间模板）
///
void getGausssianMask(cv::Mat& Mask, cv::Size wsize, double spaceSigma) {
Mask.create(wsize, CV_64F);
int h = wsize.height;
int w = wsize.width;
int center_h = (h - 1) / 2;
int center_w = (w - 1) / 2;
double sum = 0.0;
double x, y;
for (int i = 0; i < h; ++i) {
y = pow(i - center_h, 2);
double* Maskdate = Mask.ptr(i);
for (int j = 0; j < w; ++j) {
x = pow(j - center_w, 2);
double g = exp(-(x + y) / (2 * spaceSigma * spaceSigma));
Maskdate[j] = g;
sum += g;
}
}
}
//双边滤波
///
void bilateralfiter(cv::Mat& src, cv::Mat& dst, cv::Size wsize, double spaceSigma, double colorSigma) {
cv::Mat spaceMask;
std::vector colorMask;
cv::Mat Mask0 = cv::Mat::zeros(wsize, CV_64F);
cv::Mat Mask1 = cv::Mat::zeros(wsize, CV_64F);
cv::Mat Mask2 = cv::Mat::zeros(wsize, CV_64F);
getGausssianMask(spaceMask, wsize, spaceSigma);//空间模板
getColorMask(colorMask, colorSigma);//值域模板
int hh = (wsize.height - 1) / 2;
int ww = (wsize.width - 1) / 2;
dst.create(src.size(), src.type());
//边界填充
cv::Mat Newsrc;
cv::copyMakeBorder(src, Newsrc, hh, hh, ww, ww, cv::BORDER_REPLICATE);//边界复制;
for (int i = hh; i < src.rows + hh; ++i) {
for (int j = ww; j < src.cols + ww; ++j) {
double sum[3] = { 0 };
int graydiff[3] = { 0 };
double space_color_sum[3] = { 0.0 };
for (int r = -hh; r <= hh; ++r) {
for (int c = -ww; c <= ww; ++c) {
if (src.channels() == 1) {
int centerPix = Newsrc.at(i, j);
int pix = Newsrc.at(i + r, j + c);
graydiff[0] = abs(pix - centerPix);
double colorWeight = colorMask[graydiff[0]];
Mask0.at(r + hh, c + ww) = colorWeight * spaceMask.at(r + hh, c + ww);//滤波模板
space_color_sum[0] = space_color_sum[0] + Mask0.at(r + hh, c + ww);
}
else if (src.channels() == 3) {
cv::Vec3b centerPix = Newsrc.at(i, j);
cv::Vec3b bgr = Newsrc.at(i + r, j + c);
graydiff[0] = abs(bgr[0] - centerPix[0]); graydiff[1] = abs(bgr[1] - centerPix[1]); graydiff[2] = abs(bgr[2] - centerPix[2]);
double colorWeight0 = colorMask[graydiff[0]];
double colorWeight1 = colorMask[graydiff[1]];
double colorWeight2 = colorMask[graydiff[2]];
Mask0.at(r + hh, c + ww) = colorWeight0 * spaceMask.at(r + hh, c + ww);//滤波模板
Mask1.at(r + hh, c + ww) = colorWeight1 * spaceMask.at(r + hh, c + ww);
Mask2.at(r + hh, c + ww) = colorWeight2 * spaceMask.at(r + hh, c + ww);
space_color_sum[0] = space_color_sum[0] + Mask0.at(r + hh, c + ww);
space_color_sum[1] = space_color_sum[1] + Mask1.at(r + hh, c + ww);
space_color_sum[2] = space_color_sum[2] + Mask2.at(r + hh, c + ww);
}
}
}
//滤波模板归一化
if (src.channels() == 1)
Mask0 = Mask0 / space_color_sum[0];
else {
Mask0 = Mask0 / space_color_sum[0];
Mask1 = Mask1 / space_color_sum[1];
Mask2 = Mask2 / space_color_sum[2];
}
for (int r = -hh; r <= hh; ++r) {
for (int c = -ww; c <= ww; ++c) {
if (src.channels() == 1) {
sum[0] = sum[0] + Newsrc.at(i + r, j + c) * Mask0.at(r + hh, c + ww); //滤波
}
else if (src.channels() == 3) {
cv::Vec3b bgr = Newsrc.at(i + r, j + c); //滤波
sum[0] = sum[0] + bgr[0] * Mask0.at(r + hh, c + ww);//B
sum[1] = sum[1] + bgr[1] * Mask1.at(r + hh, c + ww);//G
sum[2] = sum[2] + bgr[2] * Mask2.at(r + hh, c + ww);//R
}
}
}
for (int k = 0; k < src.channels(); ++k) {
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (src.channels() == 1)
{
dst.at(i - hh, j - ww) = static_cast(sum[0]);
}
else if (src.channels() == 3)
{
cv::Vec3b bgr = { static_cast(sum[0]), static_cast(sum[1]), static_cast(sum[2]) };
dst.at(i - hh, j - ww) = bgr;
}
}
}
}
int main(int argc, char** argv)
{
Mat src = imread("E:\\Lena.jpg");
imshow("原图", src);
Mat dst = src.clone();
bilateralfiter(src, dst, Size(23,23), 3 * 2, 3 / 2);
imshow("双边滤波", dst);
waitKey();
return 0;
}
Mat src; Mat dst;
int main(int argc, char** argv)
{
Mat src = imread("E:\\Lena.jpg");
imshow("原图", src);
dst = src.clone();
blur(src, dst, Size(3, 3), Point(-1, -1));
imshow("均值滤波", src);
GaussianBlur(src, dst, Size(3,3), 0, 0);
imshow("高斯滤波", src);
medianBlur(src, dst, 3);
imshow("中值滤波", src);
bilateralFilter(src, dst, 3, 3 * 2, 3 / 2);
imshow("双边滤波", src);
waitKey();
return 0;
}
4. 总结
| 滤波器种类 | 基本原理 | 特点 |
|---|---|---|
| 均值滤波 | 使用模板内所有像素的平均值代替模板中心像素灰度值 | 易收到噪声的干扰，不能完全消除噪声，只能相对减弱噪声 |
| 中值滤波 | 计算模板内所有像素中的中值，并用所计算出来的中值体改模板中心像素的灰度值 | 对噪声不是那么敏感，能够较好的消除椒盐噪声，但是容易导致图像的不连续性 |
| 高斯滤波 | 对图像邻域内像素进行平滑时，邻域内不同位置的像素被赋予不同的权值 | 对图像进行平滑的同时，同时能够更多的保留图像的总体灰度分布特征 |
| 双边滤波 | 通俗来讲就是双边滤波模板主要有两个模板生成，第一个是高斯模板，第二个是以灰度级的差值作为函数系数生成的模板，然后这两个模板点乘就得到了最终的双边滤波模板 | 同时考虑空间与信息和灰度相似性，达到保边去噪的目的，具有简单、非迭代、局部处理的特点 |