深度学习教程(6) | 神经网络优化算法（吴恩达·完整版）

• 作者：韩信子@ShowMeAI
• 教程地址：https://www.showmeai.tech/tutorials/35
• 本文地址：https://www.showmeai.tech/article-detail/217
• 声明：版权所有，转载请联系平台与作者并注明出处
• 收藏ShowMeAI查看更多精彩内容

---

本系列为吴恩达老师《深度学习专项课程(Deep Learning Specialization)》学习与总结整理所得，对应的课程视频可以在这里查看。

引言

在ShowMeAI前一篇文章 深度学习的实用层面 中我们对以下内容进行了介绍：

• Train / Dev / Test sets的切分和比例选择
• Bias和Variance的相关知识
• 防止过拟合的方法：L2正则化和Dropout
• 规范化输入以加快梯度下降速度和精度
• 梯度消失和梯度爆炸的原因及处理方法
• 梯度检查

本篇内容展开介绍深度神经网络中的一些优化算法，通过使用这些技巧和方法来提高神经网络的训练速度和精度。

1.Batch梯度下降法

Batch梯度下降法(批梯度下降法)是最常用的梯度下降形式，它是基于整个训练集的梯度下降算法，在更新参数时使用所有的样本来进行更新。

对整个训练集进行梯度下降法的时候，我们必须处理整个训练数据集，然后才能进行一步梯度下降，即每一步梯度下降法需要对整个训练集进行一次处理，如果训练数据集很大的时候，处理速度就会比较慢。

但是如果每次处理训练数据的一部分，基于这个子集进行梯度下降法，算法迭代速度会更快。而处理的这些一小部分训练子集即称为Mini-Batch，这个算法也就是我们说的Mini-Batch梯度下降法。

2.Mini-Batch梯度下降法

Mini-Batch梯度下降法(小批量梯度下降法)每次同时处理单个的Mini-Batch，其他与Batch梯度下降法一致。

使用Batch梯度下降法，对整个训练集的一次遍历只能做一个梯度下降；而使用Mini-Batch梯度下降法，对整个训练集的一次遍历(称为一个epoch)能做Mini-Batch个数个梯度下降。之后，可以一直遍历训练集，直到最后收敛到一个合适的精度。

Batch梯度下降法和Mini-Batch梯度下降法代价函数的变化趋势如上图所示：

• 使用Batch gradient descent，随着迭代次数增加，cost是不断减小的。
• 使用Mini-batch gradient descent，随着在不同的mini-batch上迭代训练，cost并不是单调下降，而是振荡下降的，最终也能得到较低的cost值。出现细微振荡的原因是不同的mini-batch之间是有差异的。例如可能第一个子集$(X^{\{1\}},Y^{\{1\}})$是好的子集，而第二个子集$(X^{\{2\}},Y^{\{2\}})$包含了一些噪声noise。出现细微振荡是正常的。

2.1 Batch大小及影响

我们在训练神经网络的时候，使用mini-batch gradient descent，经常要指定一个batch批次的样本数量。而不同的batch大小会影响训练的过程，其中有2个特例，mini-batch gradient descent会退化为不同的算法：

• Mini-Batch的大小为1，即是随机梯度下降法(stochastic gradient descent)，每个样本都是独立的Mini-Batch。
• Mini-Batch的大小为$m$(数据集大小)，即是Batch梯度下降法。

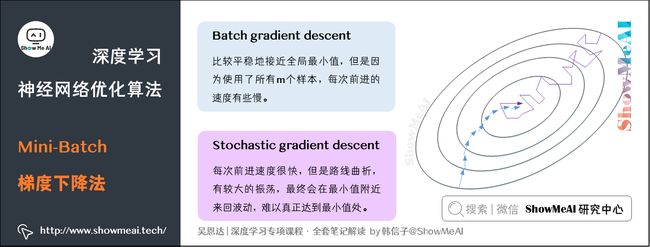
如上图，我们对比一下Batch gradient descent和Stachastic gradient descent的梯度下降曲线。

• 图中蓝色的线代表Batch gradient descent。Batch gradient descent会比较平稳地接近全局最小值，但是因为使用了所有m个样本，每次前进的速度有些慢。
• 图中紫色的线代表Stochastic gradient descent。Stochastic gradient descent每次前进速度很快，但是路线曲折，有较大的振荡，最终会在最小值附近来回波动，难以真正达到最小值处。而且在数值处理上就不能使用向量化的方法来提高运算速度。

(1) Batch梯度下降法（Batch gradient descent）

• 对所有 m 个训练样本执行一次梯度下降，每一次迭代时间较长，训练过程慢。
• 相对噪声低一些，幅度也大一些。
• 成本函数总是向减小的方向下降。

(2) 随机梯度下降法（Stochastic gradient descent）

• 对每一个训练样本执行一次梯度下降，训练速度快，但丢失了向量化带来的计算加速。
• 有很多噪声，减小学习率可以适当。
• 成本函数总体趋势向全局最小值靠近，但永远不会收敛，而是一直在最小值附近波动。

(3) Mini-Batch gradient descent

实际使用中，batch size不能设置得太大（会倾向于Batch gradient descent），也不能设置得太小（倾向于Stochastic gradient descent）。

选择一个1的合适的大小进行Mini-Batch梯度下降，可以实现快速学习，也应用了向量化带来的好处，且成本函数的下降处于前两者之间。

mini-batch gradient descent的梯度下降曲线如图绿色曲线所示，每次前进速度较快，且振荡较小，基本能接近全局最小值。

2.2 Batch大小的选择

吴恩达老师也给出了一些关于batch大小选择的经验：

• 训练样本量小（如$m\le 2000$），选择Batch梯度下降法。
• 训练样本量大，选择Mini-Batch梯度下降法。
• 与计算机的信息存储方式相适应，代码在Batch大小为2的幂次时运行要快一些，典型的大小为$2^6$、$2^7$、…、$2^9$。
• Batch的大小要匹配CPU/GPU内存。

Batch的大小是重要的超参数，需要根据经验快速尝试，找到能够最有效地减少成本函数的值。

2.3 获得Mini-Batch的步骤

前面提到了batch大小的选择方法，当我们确定batch大小后，在应用mini-batch梯度下降算法时，可以通过以下方式获得1个Batch的数据：

• 将数据集打乱
• 按照既定的大小分割数据集

其中打乱数据集的代码：

# 获得样本数量
m = X.shape[1] 
# 对m个样本进行乱序
permutation = list(np.random.permutation(m))
# 取出洗牌之后的样本特征和标签
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))

（上述python代码使用到numpy工具库，想了解更多的同学可以查看ShowMeAI的 图解数据分析 系列中的numpy教程，也可以通过ShowMeAI制作的 numpy速查手册 快速了解其使用方法）

代码解读：

np.random.permutation与np.random.shuffle有两处不同：

• 如果传给permutation一个矩阵，它会返回一个洗牌后的矩阵副本；而shuffle只是对一个矩阵进行洗牌，没有返回值。
• 如果传入一个整数，它会返回一个洗牌后的arange。

2.4 符号表示

在进一步讲解优化算法之前，我们来对数学标记做一个统一和说明：

• 我们使用小括号上标$i$表示训练集里的值，$x^{(i)}$是第$i$个训练样本。
• 我们使用中括号上标$l$表示神经网络的层数，$z^{[l]}$表示神经网络中第$l$层的$z$值。
• 我们使用上标$t$来代表不同的Batch数据，即$X^t$、$Y^t$。

3.指数加权平均

下面我们将介绍指数加权平均（Exponentially weighted averages）的概念。

举个例子，记录半年内伦敦市的气温变化，并在二维平面上绘制出来，如下图所示：

看上去，温度数据似乎有noise，而且抖动较大。如果我们希望看到半年内气温的整体变化趋势，可以通过「移动平均」（moving average）的方法来对每天气温进行平滑处理。

例如我们可以设$V_0=0$，当成第0天的气温值。

第一天的气温与第0天的气温有关：

$$V_1=0.9V_0+0.1{\theta }_1$$

第二天的气温与第一天的气温有关：

$$\begin{array}{rl}{V}_2& =0.9V_1+0.1{\theta }_2\\ & =0.9(0.9V_0+0.1{\theta }_1)+0.1{\theta }_2\\ & =0.9^2{V}_0+0.9\cdot 0.1{\theta }_1+0.1{\theta }_2\end{array}$$

第三天的气温与第二天的气温有关：

$$\begin{array}{rl}{V}_3& =0.9V_2+0.1{\theta }_3\\ & =0.9(0.9^2{V}_0+0.9\cdot 0.1{\theta }_1+0.1{\theta }_2)+0.1{\theta }_3\\ & =0.9^3{V}_0+0.9^2\cdot 0.1{\theta }_1+0.9\cdot 0.1{\theta }_2+0.1{\theta }_3\end{array}$$

即第$t$天与第$t-1$天的气温迭代关系为：

经过「移动平均」（moving average）处理得到的气温如下图红色曲线所示：

这种滑动平均算法称为指数加权平均（exponentially weighted average）。根据前面的例子，我们可以看到它的推导公式一般形式为：$V_t=\beta V_{t-1}+(1-\beta ){\theta }_t$。

其中指数加权平均的天数由$\beta$值决定，近似表示为$\frac{1}{1-\beta }$。上面的例子中：

• 当$\beta =0.9$，则$\frac{1}{1-\beta }=10$，表示将前10天进行指数加权平均。
• 当$\beta =0.98$，则$\frac{1}{1-\beta }=50$，表示将前50天进行指数加权平均。

$\beta$值越大，则指数加权平均的天数越多，平均后的趋势线就越平缓，但是同时也会向右平移。上图中绿色曲线和橙色曲线分别表示了$\beta =0.98$和$\beta =0.5$时，指数加权平均的结果。

公式解释：

这里的$\frac{1}{1-\beta }$是怎么来的呢？就标准数学公式来说，指数加权平均算法跟之前所有天的数值都有关系。

但是指数是衰减的，一般认为衰减到$\frac{1}{e}$就可以忽略不计了。因此，根据之前的推导公式，我们只要证明${\beta }^{\frac{1}{1-\beta }}=\frac{1}{e}$就好了。

令$\frac{1}{1-\beta }=N$，$N>0$，则$\beta =1-\frac{1}{N}$，$\frac{1}{N}<1$。即证明转化为 $(1-\frac{1}{N}{)}^N=\frac{1}{e}$

显然，当$N>>0$时，上述等式是近似成立的。这就简单解释了为什么指数加权平均的天数的计算公式为$\frac{1}{1-\beta }$。

综上，**指数加权平均(Exponentially Weight Average)**是一种常用的序列数据处理方式，计算公式为：

$$S_t=\{\begin{array}{ll}{Y}_1,& t=1\\ \beta S_{t-1}+(1-\beta )Y_t,& t>1\end{array}$$

其中$Y_t$为$t$下的实际值，$S_t$为$t$下加权平均后的值，$\beta$为权重值。

指数加权平均数在统计学中被称为“指数加权移动平均值”。

3.1 理解指数平均加权

我们将指数加权平均公式的一般形式写下来：

$$\begin{array}{rl}{V}_t& =\beta V_{t-1}+(1-\beta ){\theta }_t\\ & =(1-\beta ){\theta }_t+(1-\beta )\cdot \beta \cdot {\theta }_{t-1}+(1-\beta )\cdot {\beta }^2\cdot {\theta }_{t-2}+\cdots +(1-\beta )\cdot {\beta }^{t-1}\cdot {\theta }_1+{\beta }^t\cdot V_0\end{array}$$

观察上述推导得到的计算公式，其中：

• ${\theta }_t$,${\theta }_{t-1}$,${\theta }_{t-2}$,…,${\theta }_1$是原始数据值。
• $(1-\beta )$,$(1-\beta )\beta$,$(1-\beta ){\beta }^2$,…,$(1-\beta ){\beta }^{t-1}$是类似指数曲线，从右向左，呈指数下降的。

如果我们把每个时间点的$\theta$和衰减指数写成向量形式，则最终指数加权平均结果$V_t$相当于两者的点乘。将原始数据值与衰减指数点乘，相当于做了指数衰减，随距离越远衰减越厉害（注意到$\beta$小于1），有如下结论：

• 离得越近的数据点，影响越大，离得越远的数据点，影响越小。

当$\beta =0.9$时，

$$v_{100}=0.9v_{99}+0.1{\theta }_{100}$$

$$v_{99}=0.9v_{98}+0.1{\theta }_{99}$$

$$v_{98}=0.9v_{97}+0.1{\theta }_{98}$$

展开：

$$v_{100}=0.1{\theta }_{100}+0.1\ast 0.9{\theta }_{99}+0.1\ast {(0.9)}^2{\theta }_{98}+\dots$$

其中，${\theta }_i$指第$i$天的实际数据。所有$\theta$前面的系数(不包括0.1)相加起来为1或者接近于1，这些系数被称作偏差修正(Bias Correction)。

根据函数极限的一条定理：

$$\underset{\beta \to 0}{\lim }(1-\beta {)}^{\frac{1}{\beta }}=\frac{1}{e}\approx 0.368$$

当$\beta =0.9$时，可以当作把过去10天的气温指数加权平均作为当日的气温，因为10天后权重已经下降到了当天的1/3左右。同理，当$\beta =0.98$时，可以把过去50天的气温指数加权平均作为当日的气温。

因此，在计算当前时刻的平均值时，只需要前一天的平均值和当前时刻的值。

$$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$$

在实际代码中，只需要不断迭代赋值更新$v$即可：

$$v:=\beta v+(1-\beta ){\theta }_t$$

指数平均加权并不是最精准的计算平均数的方法，你可以直接计算过去10天或50天的平均值来得到更好的估计，但缺点是保存数据需要占用更多内存，执行更加复杂，计算成本更加高昂。

指数加权平均数公式的好处之一在于它只需要一行代码，且占用极少内存，因此效率极高，且节省成本。

3.2 指数平均加权的偏差修正

当$\beta =0.98$时，前面提到的气温示例，指数加权平均结果如绿色曲线。但实际上真实曲线如紫色曲线所示：

紫色曲线与绿色曲线的区别是，紫色曲线开始的时候相对较低一些。因为开始时设置$v_0=0$，所以初始值会相对小一些，直到后面受前面的影响渐渐变小，趋于正常。

修正这种问题的方法是进行偏移校正（bias correction），即在每次计算完$v_t$后，对$v_t$进行下式处理：

$$V_t=\frac{V_t}{1-{\beta }^t}$$

换算到迭代公式中，即有$v_t=\frac{\beta v_{t-1}+(1-\beta ){\theta }_t}{1-{\beta }^t}$。

观察上式：随着$t$的增大，$\beta$的$t$次方趋近于0。因此当$t$很大的时候，偏差修正几乎没有作用，但是在前期学习可以帮助更好的预测数据。

4.动量梯度下降法

4.1 从指数加权平均到动量梯度下降

大家已经了解了指数加权平均，现在我们回到神经网络优化算法，介绍一下动量梯度下降算法，其速度要比传统的梯度下降算法快很多。做法是在每次训练时，计算梯度的指数加权平均数，并利用该值来更新权重$W$和常数项$b$。

具体过程为：for l = 1, .. , L

$$v_{d{W}^{[l]}}=\beta v_{d{W}^{[l]}}+(1-\beta )d{W}^{[l]}$$

$$v_{d{b}^{[l]}}=\beta v_{d{b}^{[l]}}+(1-\beta )d{b}^{[l]}$$

$$W^{[l]}:=W^{[l]}-\alpha v_{d{W}^{[l]}}$$

$$b^{[l]}:=b^{[l]}-\alpha v_{d{b}^{[l]}}$$

其中，将动量衰减参数$\beta$设置为0.9是超参数的一个常见且效果不错的选择。当$\beta$被设置为0时，显然就成了Batch梯度下降法。

4.2 梯度下降 vs 动量梯度下降

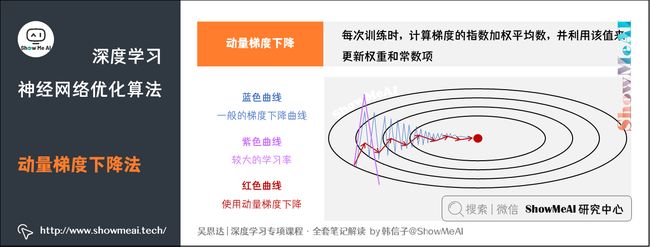
我们用下图来对比一下优化算法的优化过程

图中：

• 蓝色曲线：使用一般的梯度下降的优化过程，由于存在上下波动，减缓了梯度下降的速度，因此只能使用一个较小的学习率进行迭代。
• 紫色曲线：使用一般梯度下降+较大的学习率，结果可能偏离函数的范围。
• 红色曲线：使用动量梯度下降，通过累加过去的梯度值来减少抵达最小值路径上的波动，加速了收敛，因此在横轴方向下降得更快。

当前后梯度方向一致时，动量梯度下降能够加速学习；而前后梯度方向不一致时，动量梯度下降能够抑制震荡。

另外，在10次迭代之后，移动平均已经不再是一个具有偏差的预测。因此实际在使用梯度下降法或者动量梯度下降法时，不会同时进行偏差修正。

补充：在其它文献资料中，动量梯度下降还有另外一种写法：

$V_{dW}=\beta V_{dW}+dW$

$V_{db}=\beta V_{db}+db$

即消去了$dW$和$db$前的系数$(1-\beta )$。这样简化了表达式，但是学习因子$\alpha$相当于变成了$\frac{\alpha }{1-\beta }$，表示$\alpha$也受$\beta$的影响。从效果上来说，这种写法也是可以的，但是不够直观，且调参涉及到$\alpha$，不够方便。所以，实际应用中，推荐第一种动量梯度下降的表达式。

动量梯度下降法的形象解释

将成本函数想象为一个碗状，从顶部开始运动的小球向下滚，其中$dw$，$db$想象成球的加速度；而$v_{dw}$、$v_{db}$相当于速度。

小球在向下滚动的过程中，因为加速度的存在速度会变快，但是由于$\beta$的存在，其值小于1，可以认为是摩擦力，所以球不会无限加速下去。

5.RMSProp 算法

RMSProp(Root Mean Square Propagation，均方根传播)是另外一种优化梯度下降速度的算法，它在对梯度进行指数加权平均的基础上，引入平方和平方根。具体过程为(省略了$l$)：

$$s_{dw}=\beta s_{dw}+(1-\beta )(dw{)}^2$$

$$s_{db}=\beta s_{db}+(1-\beta )(db{)}^2$$

$$w:=w-\alpha \frac{dw}{\sqrt{s_{dw}+ϵ}}$$

$$b:=b-\alpha \frac{db}{\sqrt{s_{db}+ϵ}}$$

其中，$\epsilon$是一个实际操作时加上的较小数(例如$10^{-8}$)，为了防止分母太小而导致的数值不稳定。

如图所示，蓝色轨迹代表初始的移动，可以看到在$b$方向上走得比较陡峭(即$db$较大)，相比起来$dw$较小，这影响了优化速度。

因此，在采用RMSProp算法后，由于$(dw{)}^2$较小、$(db{)}^2$较大，进而$s_{dw}$也会较小、$s_{db}$也会较大，最终使得$\frac{dw}{\sqrt{s_{dw}+\epsilon }}$较大，而$\frac{db}{\sqrt{s_{db}+\epsilon }}$较小。后面的更新就会像绿色轨迹一样，明显好于蓝色的更新曲线。RMSProp减小某些维度梯度更新波动较大的情况，使下降速度变得更快。

RMSProp有助于减少抵达最小值路径上的摆动，并允许使用一个更大的学习率$\alpha$，从而加快算法学习速度。并且，它和Adam优化算法已被证明适用于不同的深度学习网络结构。

注意，$\beta$也是一个超参数。

对比原始梯度下降与RMSProp算法优化过程，如下图所示（上方为原始梯度下降，下方为RMSProp）

6.Adam 优化算法

6.1 Adam算法介绍

**Adam (Adaptive Moment Estimation，自适应矩估计)**算法结合了动量梯度下降算法和RMSprop算法，通常有超越二者单独时的效果。具体过程如下(省略了$l$)：

首先进行初始化：

$$v_{dW}=0,s_{dW}=0,v_{db}=0,s_{db}=0$$

用每一个Mini-Batch计算$dW$、$db$，第$t$次迭代时：

$$v_{dW}={\beta }_1{v}_{dW}+(1-{\beta }_1)dW$$

$$v_{db}={\beta }_1{v}_{db}+(1-{\beta }_1)db$$

$$s_{dW}={\beta }_2{s}_{dW}+(1-{\beta }_2){(dW)}^2$$

$$s_{db}={\beta }_2{s}_{db}+(1-{\beta }_2){(db)}^2$$

一般使用Adam算法时需要计算偏差修正：

$$v_{dW}^{corrected}=\frac{v_{dW}}{1-{{\beta }_1}^t}$$

$$v_{db}^{corrected}=\frac{v_{db}}{1-{{\beta }_1}^t}$$

$$s_{dW}^{corrected}=\frac{s_{dW}}{1-{{\beta }_2}^t}$$

$$s_{db}^{corrected}=\frac{s_{db}}{1-{{\beta }_2}^t}$$

所以，更新$W$、$b$时有：

$$W:=W-\alpha \frac{v_{dW}^{corrected}}{\sqrt{s_{dW}^{corrected}}+\epsilon }$$

$$b:=b-\alpha \frac{v_{db}^{corrected}}{\sqrt{s_{db}^{corrected}}+\epsilon }$$

6.2 Adam超参数的选择

Adam优化算法有很多的超参数，其中

• 学习率$\alpha$：需要尝试一系列的值，来寻找比较合适的
• ${\beta }_1$：常用的缺省值为0.9
• ${\beta }_2$：Adam算法的作者建议为0.999
• $\epsilon$：不重要，不会影响算法表现，Adam算法的作者建议为$10^{-8}$

${\beta }_1$、${\beta }_2$、$\epsilon$通常不需要调试。

对比原始梯度下降与RMSProp算法优化过程，如下图所示（上方为原始梯度下降，下方为Adam）

7.学习率衰减

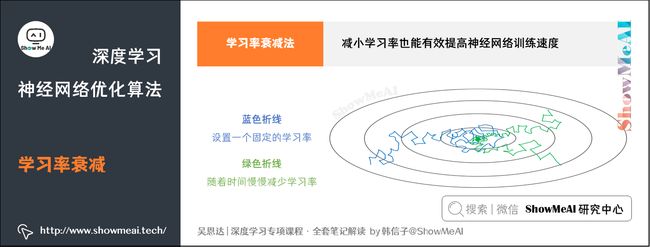
减小学习率$\alpha$也能有效提高神经网络训练速度，这种方法被称为学习率衰减法（learning rate decay）。

学习率衰减就是随着迭代次数增加，学习率$\alpha$逐渐减小。如下图示例。

① 蓝色折线表示设置一个固定的学习率$\alpha$

• 在最小值点附近，由于不同的Batch中存在一定的噪声，因此不会精确收敛，而是始终在最小值周围一个较大的范围内波动。

② 绿色折线表示随着时间慢慢减少学习率$\alpha$的大小

• 在初期$\alpha$较大时，下降的步长较大，能以较快的速度进行梯度下降；
• 后期逐步减小$\alpha$的值，即减小步长，有助于算法的收敛，更容易接近最优解。

最常用的学习率衰减方法：

$$\alpha =\frac{1}{1+decay\_rate\ast epoch\_num}\ast {\alpha }_0$$

其中，decay_rate为衰减率(超参数)，epoch_num为将所有的训练样本完整过一遍的次数。

• 指数衰减：$\alpha =0.95^{epoch\_num}\ast {\alpha }_0$
• 其他：$\alpha =\frac{k}{\sqrt{epoch\_num}}\ast {\alpha }_0$
• 离散下降

对于较小的模型，也有人会在训练时根据进度手动调小学习率。

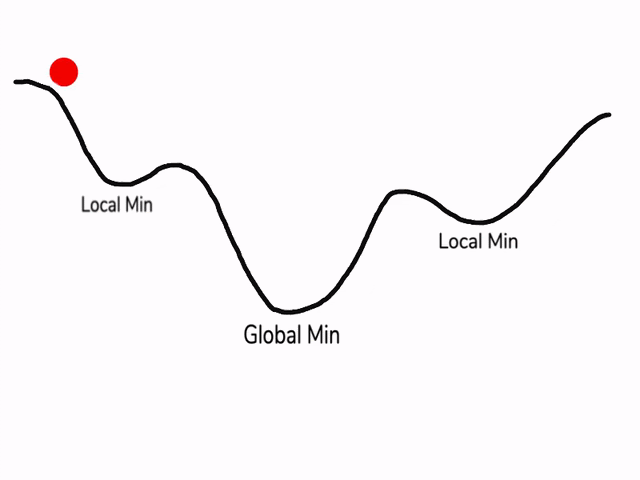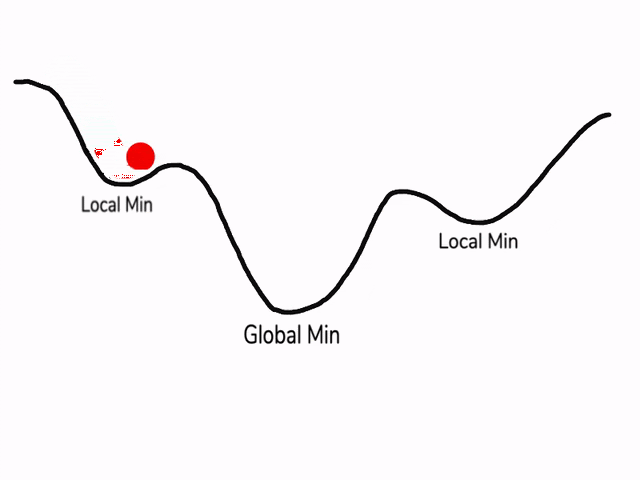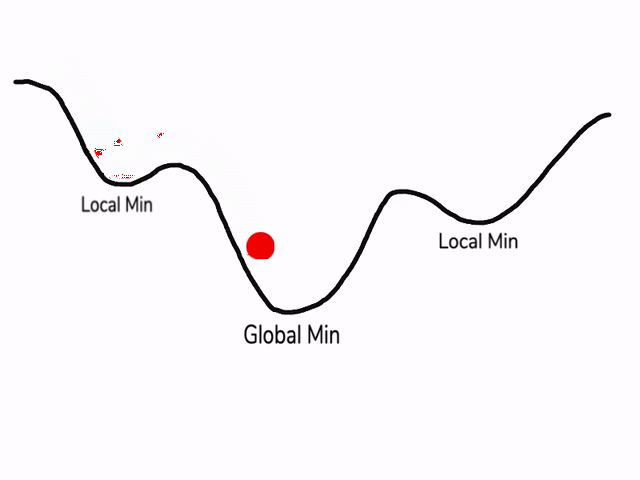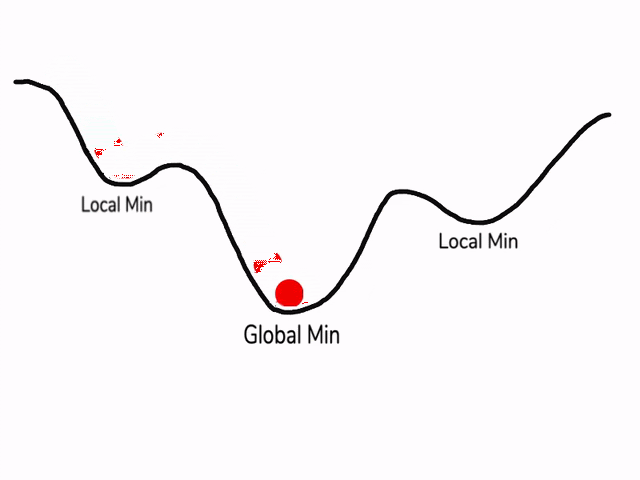
8.局部最优问题

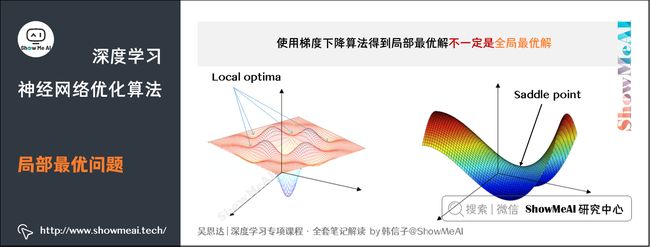
在使用梯度下降算法不断减小cost function时，可能会得到局部最优解（local optima）而不是全局最优解（global optima）。

之前我们对局部最优解的理解是形如碗状的凹槽，如图左边所示。但是在神经网络中，local optima的概念发生了变化。准确来说，大部分梯度为零的“最优点”并不是这些凹槽处，而是形如右边所示的马鞍状，称为saddle point。

所以在深度学习损失函数中，梯度为零并不能保证都是convex（极小值），也有可能是concave（极大值）。特别是在神经网络中参数很多的情况下，所有参数梯度为零的点很可能都是右边所示的马鞍状的saddle point，而不是左边那样的local optimum。

类似马鞍状的plateaus会降低神经网络学习速度。Plateaus是梯度接近于零的平缓区域，如图所示。在plateaus上梯度很小，前进缓慢，到达saddle point需要很长时间。到达saddle point后，由于随机扰动，梯度一般能够沿着图中绿色箭头，离开saddle point，继续前进，只是在plateaus上花费了太多时间。

结论：

• 在训练较大的神经网络、存在大量参数，并且成本函数被定义在较高的维度空间时，困在极差的局部最优中是不大可能的；
• 鞍点附近的平稳段会使得学习非常缓慢，而这也是动量梯度下降法、RMSProp以及Adam优化算法能够加速学习的原因，它们能帮助尽早走出平稳段。

参考资料

• 图解数据分析
• numpy速查手册

ShowMeAI系列教程推荐

• 大厂技术实现：推荐与广告计算解决方案
• 大厂技术实现：计算机视觉解决方案
• 大厂技术实现：自然语言处理行业解决方案
• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程：吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程：斯坦福CS224n课程 · 课程带学与全套笔记解读
• 深度学习与计算机视觉教程：斯坦福CS231n · 全套笔记解读

推荐文章

• ShowMeAI 深度学习教程(1) | 深度学习概论
• ShowMeAI 深度学习教程(2) | 神经网络基础
• ShowMeAI 深度学习教程(3) | 浅层神经网络
• ShowMeAI 深度学习教程(4) | 深层神经网络
• ShowMeAI 深度学习教程(5) | 深度学习的实用层面
• ShowMeAI 深度学习教程(6) | 神经网络优化算法
• ShowMeAI 深度学习教程(7) | 网络优化：超参数调优、正则化、批归一化和程序框架
• ShowMeAI 深度学习教程(8) | AI应用实践策略（上）
• ShowMeAI 深度学习教程(9) | AI应用实践策略（下）
• ShowMeAI 深度学习教程(10) | 卷积神经网络解读
• ShowMeAI 深度学习教程(11) | 经典CNN网络实例详解
• ShowMeAI 深度学习教程(12) | CNN应用：目标检测
• ShowMeAI 深度学习教程(13) | CNN应用：人脸识别和神经风格转换
• ShowMeAI 深度学习教程(14) | 序列模型与RNN网络
• ShowMeAI 深度学习教程(15) | 自然语言处理与词嵌入
• ShowMeAI 深度学习教程(16) | Seq2seq序列模型和注意力机制