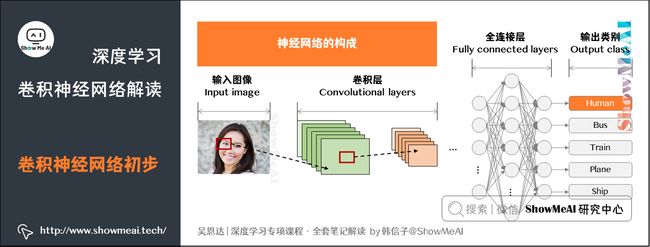
深度学习教程(10) | 卷积神经网络解读(吴恩达·完整版)
![]()
- 作者:韩信子@ShowMeAI
- 教程地址:http://www.showmeai.tech/tutorials/35
- 本文地址:http://www.showmeai.tech/article-detail/221
- 声明:版权所有,转载请联系平台与作者并注明出处
- 收藏ShowMeAI查看更多精彩内容
本系列为吴恩达老师《深度学习专项课程(Deep Learning Specialization)》学习与总结整理所得,对应的课程视频可以在这里查看。
引言
在ShowMeAI前一篇文章 AI应用实践策略(下) 中我们对以下内容进行了介绍:
- 错误分析(error analysis)
- 错误标签情况及修正
- 数据分布和数据不匹配问题及解决办法
- 迁移学习
- 多任务学习
- 端到端学习
本篇开始,我们对吴恩达老师第4门课《Convolutional Neural Networks》(卷积神经网络)做总结梳理。内容主要覆盖卷积神经网络(CNN)的基本概念、模型和具体应用等。
1.计算机视觉
**计算机视觉(Computer Vision)**的高速发展标志着新型应用产生的可能,例如自动驾驶、人脸识别、创造新的艺术风格。人们对于计算机视觉的研究也催生了很多计算机视觉与其他领域的交叉成果。如下是一些典型的计算机视觉场景应用场景:
后面部分ShowMeAI会根据吴恩达老师的课程给大家讲到以下CV应用:
- 图片分类(Image Classification)
- 目标检测(Object detection)
- 神经风格转换(Neural Style Transfer)
使用传统神经网络处理机器视觉面临的一个挑战是数据的输入可能会非常大。例如一张 1000 × 1000 × 3 1000 \times 1000 \times 3 1000×1000×3 的图片,神经网络输入层的维度将高达三百万,使得网络权重 W W W 非常庞大。这样会造成两个后果:
- 神经网络结构复杂,数据量相对较少,容易出现过拟合。
- 所需内存和计算量巨大。
因此,一般的神经网络很难处理海量图像数据。解决这一问题的方法就是使用特殊结构的神经网络:卷积神经网络(Convolutional Neural Network, CNN)。
2.卷积运算
前面的文章里讲到过,神经网络由浅层到深层,分别可以检测出不同层次的信息,在计算机视觉中我们依托深度卷积神经网络,来依次学习理解图片的边缘特征、局部特征(例如眼睛、鼻子等),直至最后一层综合前面检测的特征来识别整体图像内容。
卷积运算(Convolutional Operation)是卷积神经网络最基本的组成部分。我们以边缘检测为例,来解释卷积是怎样运算的。
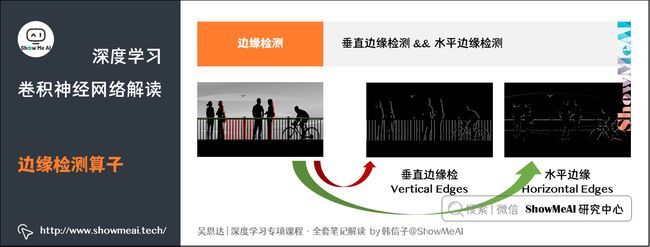
2.1 边缘检测
如下图所示,以人脸识别为例,神经网络由浅层到深层,分别可以检测出图片的边缘特征 、局部特征(例如眼睛、鼻子等)、整体面部轮廓等。
图片最常做的边缘检测有两类:垂直边缘(Vertical Edges)检测和水平边缘(Horizontal Edges)检测。
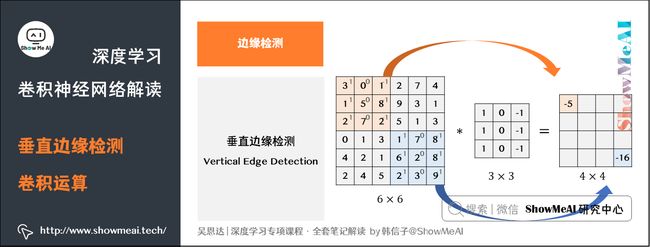
图片的边缘检测可以通过与相应滤波器进行卷积来实现。以垂直边缘检测为例,原始图片尺寸为 6 × 6 6 \times 6 6×6,中间的矩阵被称作滤波器(filter),尺寸为 3 × 3 3 \times 3 3×3,卷积后得到的图片尺寸为 4 × 4 4 \times 4 4×4,得到结果如下(数值表示灰度,以左上角和右下角的值为例):
上图只显示了卷积后的第一个值和最后一个值。卷积运算的求解过程是从左到右,由上到下,每次在原始图片矩阵中取与滤波器同等大小的一部分,每一部分中的值与滤波器中的值对应相乘后求和,将结果组成一个矩阵。
下图对应一个垂直边缘检测的例子:
如果将最右边的矩阵当作图像,那么中间一段亮一些的区域对应最左边的图像中间的垂直边缘。
这里有另一个卷积运算的动态的例子,方便理解:
图中的*表示卷积运算符号。在计算机中这个符号表示一般的乘法,而在不同的深度学习框架中,卷积操作的API定义可能不同:
- 在Python中,卷积用
conv_forward()表示; - 在Tensorflow中,卷积用
tf.nn.conv2d()表示; - 在Keras中,卷积用
Conv2D()表示。
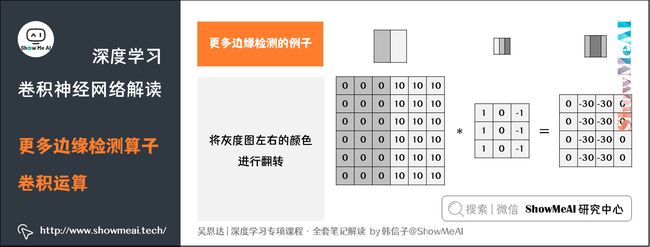
2.2 更多边缘检测的例子
如果将灰度图左右的颜色进行翻转,再与之前的滤波器进行卷积,得到的结果也有区别。实际应用中,这反映了由明变暗和由暗变明的两种渐变方式。可以对输出图片取绝对值操作,以得到同样的结果。
垂直边缘检测滤波器和水平边缘检测滤波器如下所示,其他常用的滤波器还有Sobel滤波器和Scharr滤波器,它们增加了中间行的权重,以提高结果的稳健性。
滤波器中的值还可以设置为参数,通过模型训练来得到。这样,神经网络使用反向传播算法可以学习到一些低级特征,从而实现对图片所有边缘特征的检测,而不仅限于垂直边缘和水平边缘。
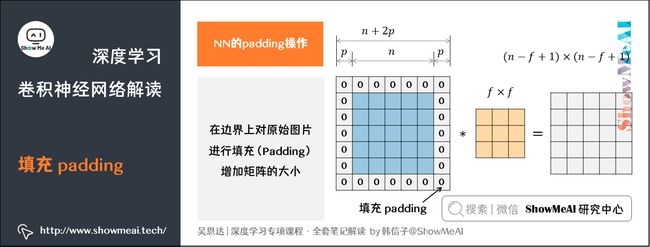
3.填充padding
观察上述卷积图片,我们假设输入图片的大小为 n × n n \times n n×n,而滤波器的大小为 f × f f \times f f×f(注意 f f f一般为奇数),则卷积后的输出图片大小为 ( n − f + 1 ) × ( n − f + 1 ) (n-f+1) \times (n-f+1) (n−f+1)×(n−f+1)。
这样的处理会带来两个问题:
- 每次卷积运算后,输出图片的尺寸缩小。
- 原始图片的角落、边缘区像素点在输出中采用较少,输出图片丢失边缘位置的很多信息。
为了解决这些问题,可以在进行卷积操作前,对原始图片在边界上进行填充(Padding),以增加矩阵的大小,保证输出的尺寸以及边缘位置信息的有效利用。我们通常用 0 0 0进行填充。
设每个方向扩展像素点数量为 p p p,则填充后原始图片的大小为 ( n + 2 p ) × ( n + 2 p ) (n+2p) \times (n+2p) (n+2p)×(n+2p),滤波器大小保持 f × f f \times f f×f不变,则输出图片大小为 ( n + 2 p − f + 1 ) × ( n + 2 p − f + 1 ) (n+2p-f+1) \times (n+2p-f+1) (n+2p−f+1)×(n+2p−f+1)。
有两种对于 p p p的设置是最常见的:
- Valid卷积:不进行填充,直接卷积。结果大小为 ( n − f + 1 ) × ( n − f + 1 ) (n-f+1) \times (n-f+1) (n−f+1)×(n−f+1)
- Same卷积:进行填充,并保证卷积后结果大小与输入一致,此时 p = f − 1 2 p = \frac{f-1}{2} p=2f−1
在计算机视觉领域, f f f通常为奇数。原因包括Same卷积中 p = f − 1 2 p = \frac{f-1}{2} p=2f−1能得到自然数结果,并且滤波器有一个便于表示其所在位置的中心点。
4.卷积步长
卷积过程中,有时需要通过填充来避免信息损失,有时也需要通过设置**步长(Stride)**来压缩一部分信息。
步长表示滤波器在原始图片的水平方向和垂直方向上每次移动的距离。之前,步长被默认为 1。而如果我们设置步长为2,则卷积过程如下图所示:
设步长stride为 s s s,padding填充大小为 p p p,输入图片大小为 n × n n \times n n×n,滤波器大小为 f × f f \times f f×f,则卷积后图片的尺寸为:
⌊ n + 2 p − f s + 1 ⌋ × ⌊ n + 2 p − f s + 1 ⌋ \biggl\lfloor \frac{n+2p-f}{s}+1 \biggr\rfloor \times \biggl\lfloor \frac{n+2p-f}{s}+1 \biggr\rfloor ⌊sn+2p−f+1⌋×⌊sn+2p−f+1⌋
上述公式中有一个向下取整的符号,用于处理商不为整数的情况。
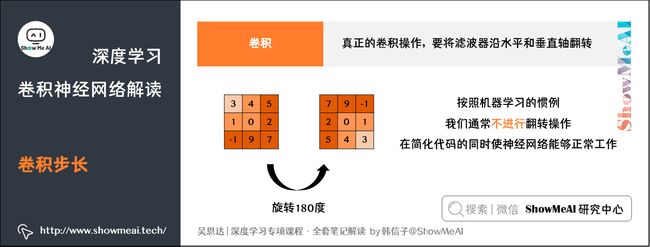
我们前面看到的「卷积」实际上是互相关(cross-correlation),而非数学意义上的卷积。真正的卷积操作在做元素乘积求和之前,要将滤波器沿水平和垂直轴翻转(相当于旋转180度)。
因为这种翻转对一般为水平或垂直对称的滤波器影响不大,按照机器学习的惯例,我们通常不进行翻转操作,在简化代码的同时使神经网络能够正常工作。
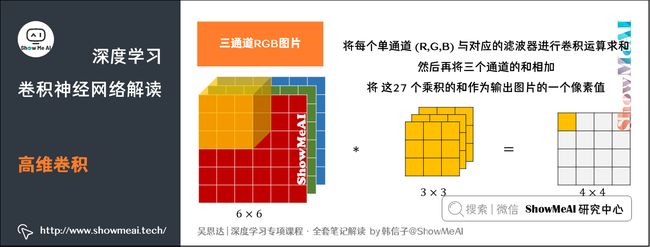
5.高维卷积
如果我们想要对三通道的RGB图片进行卷积运算,那么其对应的滤波器组也同样是三通道的。过程是将每个单通道 ( R , G , B ) (R,G,B) (R,G,B)与对应的滤波器进行卷积运算求和,然后再将三个通道的和相加,将这27个乘积的和作为输出图片的一个像素值。
实际的计算过程也同样会滑动覆盖所有输入通道和图片全部输入像素,如下动图所示:
不同通道的滤波器可以不相同。例如只检测 R R R通道的垂直边缘, G G G通道和 B B B通道不进行边缘检测,则 G G G通道和 B B B通道的滤波器全部置零。
当输入有特定的高、宽和通道数时,滤波器可以有不同的高和宽,但通道数必须和输入一致。
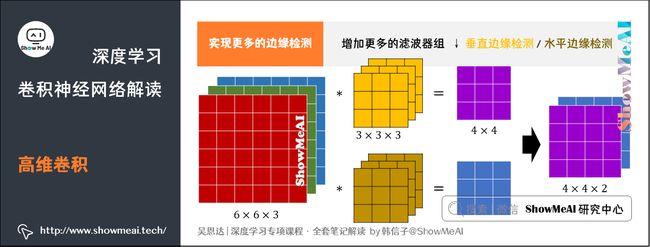
如果想同时检测垂直和水平边缘,或者更多的边缘检测,可以增加更多的滤波器组。例如第1个滤波器组实现垂直边缘检测,第2个滤波器组实现水平边缘检测。
设输入图片的尺寸为 n × n × n c n \times n \times n_c n×n×nc( n c n_c nc为通道数),滤波器尺寸为 f × f × n c f \times f \times n_c f×f×nc,则卷积后的输出图片尺寸为 ( n − f + 1 ) × ( n − f + 1 ) × n ′ c (n-f+1) \times (n-f+1) \times n\prime_c (n−f+1)×(n−f+1)×n′c, n ′ c n \prime_c n′c为滤波器组的个数。
如下动图为2个滤波器对输入进行卷积计算得到输出的过程。
6.卷积神经网络单层结构
6.1 CNN单层结构
卷积神经网络的单层结构如下所示:与上面提到的卷积过程相比较,卷积神经网络的单层结构多了激活函数(上图使用的ReLU)和偏置量b;
对比标准神经网络:
Z [ l ] = W [ l ] A [ l − 1 ] + b Z^{[l]} = W^{[l]}A^{[l-1]}+b Z[l]=W[l]A[l−1]+b
A [ l ] = g [ l ] ( Z [ l ] ) A^{[l]} = g^{[l]}(Z^{[l]}) A[l]=g[l](Z[l])
卷积神经网络把上式中 W [ l ] W^{[l]} W[l]与 A [ l − 1 ] A^{[l-1]} A[l−1]的乘积运算换成了卷积运算,滤波器的取值对应着权重 W [ l ] W^{[l]} W[l],激活函数选择ReLU。
我们重点来看一下上图中参数的数目:每个滤波器组有 3 × 3 × 3 = 27 3 \times 3 \times 3 = 27 3×3×3=27个参数,还有1个偏移量b,则每个滤波器组有 27 + 1 = 28 27+1=28 27+1=28个参数,两个滤波器组总共包含 28 × 2 = 56 28 \times 2 = 56 28×2=56个参数。
而且大家会发现,一旦确定滤波器组,则参数数量就确定了,它与输入图片尺寸无关。大尺寸的图片也并不会在卷积层带来巨大的参数量。
一张 1000 × 1000 × 3 1000 \times 1000 \times 3 1000×1000×3的图片,标准神经网络输入层的维度将达到3百万,而在CNN中,参数数目只由滤波器组决定,数目相对来说要少得多,在如上的卷积神经网络层结构中,依旧只需要 56 56 56个参数。
6.2 CNN标记符号梳理总结
为了更规范,我们来约定一下CNN单层结构标记符号,设 l l l层为卷积层:
- f [ l ] f^{[l]} f[l]:滤波器的高(或宽)
- p [ l ] p^{[l]} p[l]:填充长度
- s [ l ] s^{[l]} s[l]:步长
- n c [ l ] n^{[l]}_c nc[l]:滤波器组的数量
- 输入维度: n H [ l − 1 ] × n W [ l − 1 ] × n c [ l − 1 ] n^{[l-1]}_H \times n^{[l-1]}_W \times n^{[l-1]}_c nH[l−1]×nW[l−1]×nc[l−1]
其中 n H [ l − 1 ] n^{[l-1]}_H nH[l−1]表示输入图片的高, n W [ l − 1 ] n^{[l-1]}_W nW[l−1]表示输入图片的宽。之前的示例中输入图片的高和宽都相同,但是实际中可以是不同的,我们在这里加上下标予以区分。
- 每个滤波器组的维度: f [ l ] × f [ l ] × n c [ l − 1 ] f^{[l]} \times f^{[l]} \times n^{[l-1]}_c f[l]×f[l]×nc[l−1]。其中 n c [ l − 1 ] n^{[l-1]}_c nc[l−1]为输入图片通道数(也称深度)。
- 权重维度: f [ l ] × f [ l ] × n c [ l − 1 ] × n c [ l ] f^{[l]} \times f^{[l]} \times n^{[l-1]}_c \times n^{[l]}_c f[l]×f[l]×nc[l−1]×nc[l]
- 偏置维度: 1 × 1 × 1 × n c [ l ] 1 \times 1 \times 1 \times n^{[l]}_c 1×1×1×nc[l]
- 输出维度: n H [ l ] × n W [ l ] × n c [ l ] n^{[l]}_H \times n^{[l]}_W \times n^{[l]}_c nH[l]×nW[l]×nc[l]。
其中
n H [ l ] = ⌊ n H [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋ n^{[l]}_H = \biggl\lfloor \frac{n^{[l-1]}_H+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \biggr\rfloor nH[l]=⌊s[l]nH[l−1]+2p[l]−f[l]+1⌋
n W [ l ] = ⌊ n W [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋ n^{[l]}_W = \biggl\lfloor \frac{n^{[l-1]}_W+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \biggr\rfloor nW[l]=⌊s[l]nW[l−1]+2p[l]−f[l]+1⌋
对于m个样本的向量化运算,相应的输出维度为:
m × n H [ l ] × n W [ l ] × n c [ l ] m \times n^{[l]}_H \times n^{[l]}_W \times n^{[l]}_c m×nH[l]×nW[l]×nc[l]
7.简单卷积网络示例
下图为1个简单的CNN模型,我们来分析一下它的结构:
图示网络中, a [ 3 ] a^{[3]} a[3]的维度为 7 × 7 × 40 7 \times 7 \times 40 7×7×40,将其平展成1960维的单列形式,然后连接最后的输出层。输出层可以是一个神经元,即二元分类(logistic);也可以是多个神经元,即多分类(Softmax)。最后得到预测输出 y ^ \hat y y^。
在典型的CNN结构里,随着神经网络计算深度不断加深,输入的高度和宽度 n H [ l ] n^{[l]}_H nH[l]、 n W [ l ] n^{[l]}_W nW[l]一般逐渐减小,而 n c [ l ] n^{[l]}_c nc[l]在增加。
卷积神经网络包含有三种典型的层结构:
- 卷积层(Convolution layer)
- 池化层(Pooling layer,也有译作「汇合层」)
- 全连接层(Fully Connected layer)
仅用卷积层也有可能构建出很好的神经网络,但很多神经网络还是会添加池化层和全连接层,它们更容易设计。
8.池化层
很多CNN中都会包含Pooling layers池化层,池化层的作用是缩减模型的大小,提高计算速度,同时减小噪声提高所提取特征的稳健性。
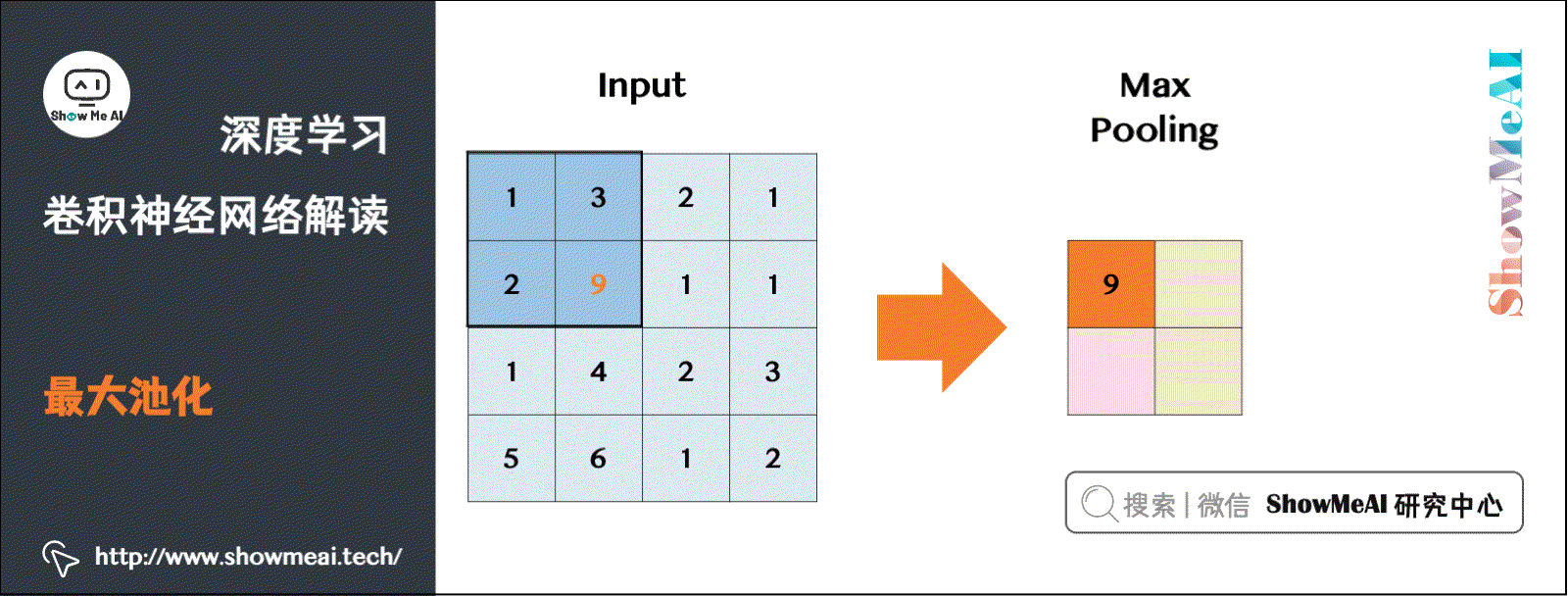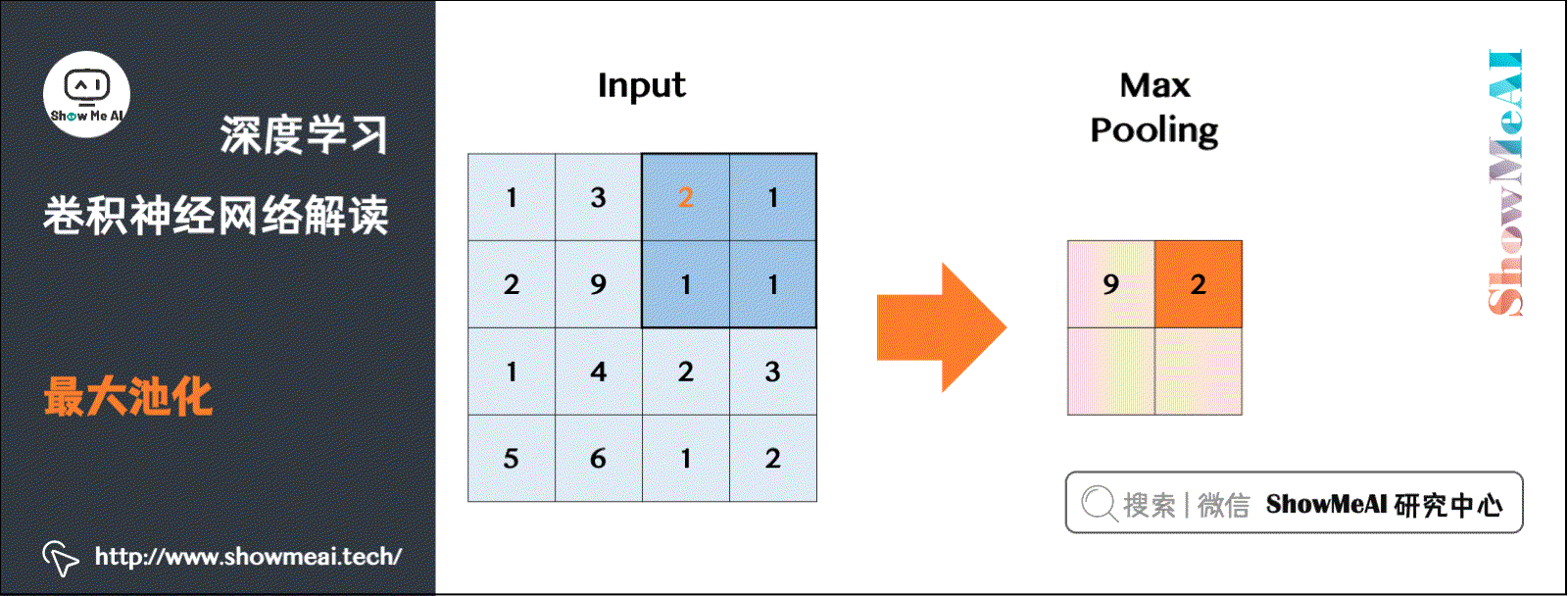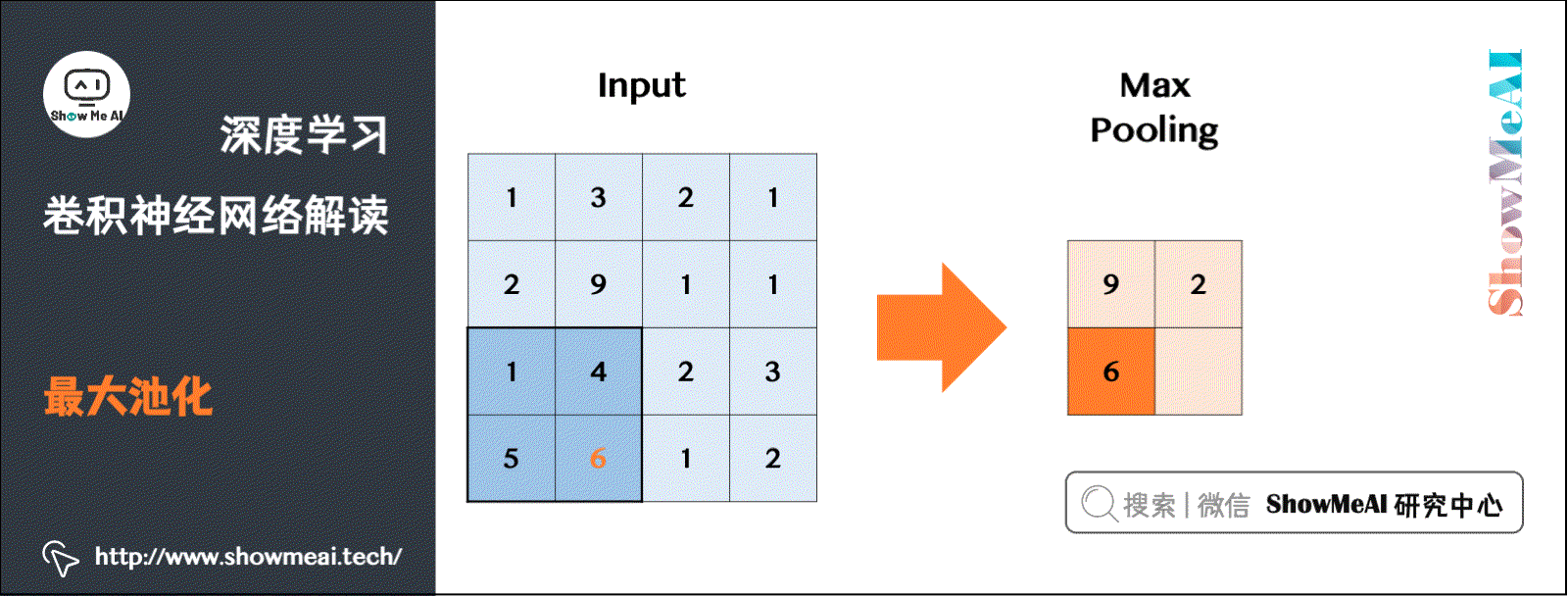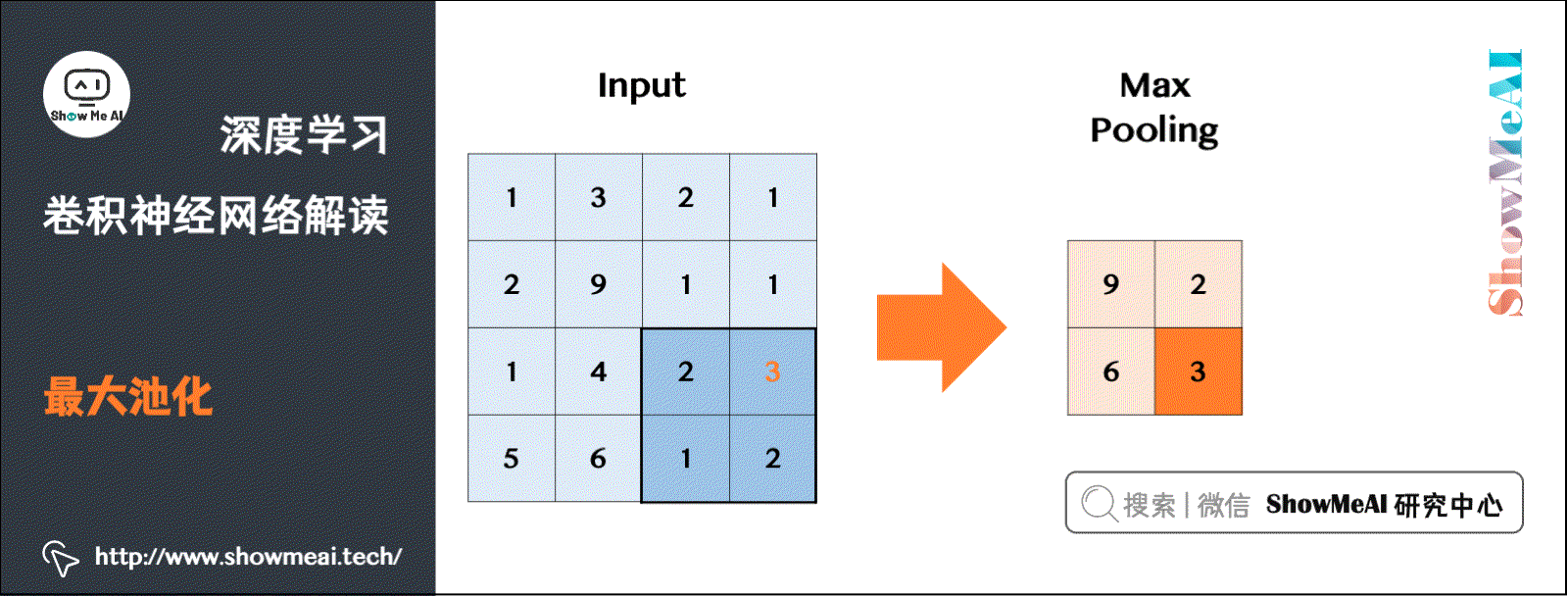
8.1 最大池化Max Pooling
有不同的池化操作,比较常见的一种叫做最大池化(Max Pooling)。将输入拆分成不同的区域,输出的每个元素都是对应区域中元素的最大值,如下图所示:
类比卷积过程,上图所示的池化过程中相当于使用了一个大小 f = 2 f=2 f=2的滤波器,且池化步长 s = 2 s=2 s=2。卷积过程中的几个计算大小的公式也都适用于池化过程。如果有多个通道,那么就对每个通道分别执行计算过程。
对最大池化的一种直观解释是,元素值较大可能意味着池化过程之前的卷积过程提取到了某些特定的特征,池化过程中的最大化操作使得只要在一个区域内提取到某个特征,它都会保留在最大池化的输出中。但是,没有足够的证据证明这种直观解释的正确性,而最大池化被使用的主要原因是它在很多实验中的效果都很好。
8.2 平均池化Average Pooling
还有一种大家可能会见到的池化过程是平均池化(Average Pooling),它会对对应区域求平均值输出:
8.3 池化层总结
池化过程的特点之一是,它有一组超参数,但是并没有参数需要学习。池化过程的超参数包括滤波器的大小 f f f、步长 s s s,以及选用最大池化还是平均池化。而填充 p p p则很少用到。
池化过程的输入维度为: n H × n W × n c n_H \times n_W \times n_c nH×nW×nc
输出维度为: ⌊ n H − f s + 1 ⌋ × ⌊ n W − f s + 1 ⌋ × n c \biggl\lfloor \frac{n_H-f}{s}+1 \biggr\rfloor \times \biggl\lfloor \frac{n_W-f}{s}+1 \biggr\rfloor \times n_c ⌊snH−f+1⌋×⌊snW−f+1⌋×nc
9.卷积神经网络示例
在计算神经网络的层数时,通常只统计具有权重和参数的层,因此池化层通常和之前的卷积层共同计为一层。图中的FC3和FC4为全连接层,与标准的神经网络结构一致。整个神经网络各层的尺寸与参数如下表所示:
| 层次 | 输出维度 | 输出大小 | 参数量 |
|---|---|---|---|
| Input | (32, 32, 3) | 3072 | 0 |
| CONV1(f=5, s=1) | (28, 28, 6) | 4704 | 158 |
| POOL1 | (14, 14, 6) | 1176 | 0 |
| CONV2(f=5, s=1) | (10, 10, 16) | 1600 | 416 |
| POOL2 | (5, 5, 16) | 400 | 0 |
| FC3 | (120, 1) | 120 | 48120 |
| FC4 | (84, 1) | 84 | 10164 |
| Softmax | (10, 1) | 10 | 850 |
推荐大家通过 直观感受卷积神经网络的网站 对CNN进行调试和可视化。
10.使用卷积的原因
根据前面的知识学习,大家知道,CNN相比于标准神经网络,能更好地适应高维度的大输入,其卷积设计有效地减少了CNN的参数数量。总结如下:
-
参数共享(Parameter sharing):特征检测如果适用于图片的某个区域,那么它也可能适用于图片的其他区域。即在卷积过程中,不管输入有多大,一个特征探测器(滤波器)就能对整个输入的某一特征进行探测。
-
稀疏连接(Sparsity of connections):在每一层中,由于滤波器的尺寸限制,输入和输出之间的连接是稀疏的,每个输出值只取决于输入在局部的一小部分值。
池化的设计,在卷积之后很好地聚合了特征,通过降维来减少运算量。
另外,吴恩达老师也说明了,由于CNN参数数量较小,所需的训练样本就相对较少,因此在一定程度上不容易发生过拟合现象。并且CNN比较擅长捕捉区域位置偏移。即进行物体检测时,不太受物体在图片中位置的影响,增加检测的准确性和系统的健壮性。
参考资料
- 直观感受卷积神经网络的网站
ShowMeAI系列教程推荐
- 大厂技术实现:推荐与广告计算解决方案
- 大厂技术实现:计算机视觉解决方案
- 大厂技术实现:自然语言处理行业解决方案
- 图解Python编程:从入门到精通系列教程
- 图解数据分析:从入门到精通系列教程
- 图解AI数学基础:从入门到精通系列教程
- 图解大数据技术:从入门到精通系列教程
- 图解机器学习算法:从入门到精通系列教程
- 机器学习实战:手把手教你玩转机器学习系列
- 深度学习教程:吴恩达专项课程 · 全套笔记解读
- 自然语言处理教程:斯坦福CS224n课程 · 课程带学与全套笔记解读
- 深度学习与计算机视觉教程:斯坦福CS231n · 全套笔记解读
推荐文章
- ShowMeAI 深度学习教程(1) | 深度学习概论
- ShowMeAI 深度学习教程(2) | 神经网络基础
- ShowMeAI 深度学习教程(3) | 浅层神经网络
- ShowMeAI 深度学习教程(4) | 深层神经网络
- ShowMeAI 深度学习教程(5) | 深度学习的实用层面
- ShowMeAI 深度学习教程(6) | 神经网络优化算法
- ShowMeAI 深度学习教程(7) | 网络优化:超参数调优、正则化、批归一化和程序框架
- ShowMeAI 深度学习教程(8) | AI应用实践策略(上)
- ShowMeAI 深度学习教程(9) | AI应用实践策略(下)
- ShowMeAI 深度学习教程(10) | 卷积神经网络解读
- ShowMeAI 深度学习教程(11) | 经典CNN网络实例详解
- ShowMeAI 深度学习教程(12) | CNN应用:目标检测
- ShowMeAI 深度学习教程(13) | CNN应用:人脸识别和神经风格转换
- ShowMeAI 深度学习教程(14) | 序列模型与RNN网络
- ShowMeAI 深度学习教程(15) | 自然语言处理与词嵌入
- ShowMeAI 深度学习教程(16) | Seq2seq序列模型和注意力机制