【机器学习】LightGBM+遗传算法 调参优化

基于遗传算法改进LightGBM 

背景介绍

LightGBM作为新流绍行起来的算法模型，其发布时间短，相对前沿，且LightGBM模型较复杂，国内对LightGBM的研究尚处于应用阶段，而针对LightGBM进行改进的相关工作较少。由于参数对模型性能表现有着决定性的影响，加之LightGBM模型参数众多，因此优化LightGBM预测模型的参数对于提升其在景区产品销量预估的表现尤为重要。但模型参数的调整往往依赖于人工经验和迭代试错，且LightGBM的参数众多、意义多样（如表4-7），使得调整参数工作就显得尤为繁琐和庞大，极可能落入局部最优的调参范围，事倍功半，精度提升不高。此外，最优参数组极大程度依赖于训练样本数据，噪声的存在会影响模型学习和演算进程，降低训练模型的泛化能力和稳定性。

LightGBM部分参数情况

参数	默认取值	取值范围	说明
num_boost_round	--	[10,  +]	训练迭代次数
learning_rate	0.01	(0, 1)	学习步长
max_depth	5	[2, +]	树的最大深度
min_child_weight	5	[1, +]	最小样本权重和
bagging_fraction	1	(0, 1]	创建树的样本采样比例
feature_fraction	1	(0, 1]	创建树时特征采样比例
early_stopping_round	--	[10,  +]	提早终止训练，防止过拟合
lambda	0	{0 , 1}	指定L2正则化
alpha	0	{0 , 1}	指定L1正则化
...	...	...	...

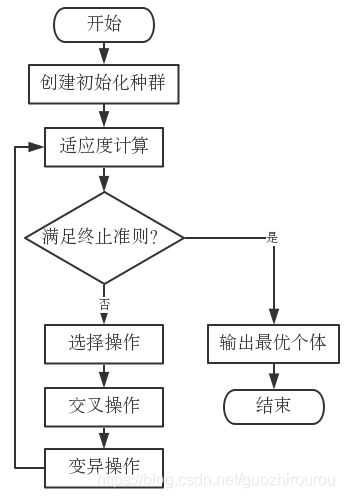
然而利用遗传算法GA的优势可以很好改善这一不足。遗传算法（Genetic Algorithm, GA）是基于进化理论和种群遗传理论，通过计算机模拟生物界自然选择和遗传的机制，利用遗传复制、交叉变异的思想，进化得到适应于指定环境下的最优成果，具有随机性、并行性和全局性，能自动的积攒全局范围内的空间信息，自适应的达到逼近最优值的状态。遗传仿生算法的出现，使其迅速在各领域如目标优化、调度方案、模式识别、机器学习等得到广泛的应用，成为了一种鲁棒性强、效率高的优化方法，

其基本算法流程如图:

遗传算法作为一种具有随机性、并行性和全局性的优化方法，其个体适应性函数（即求解问题的目标函数），能自动化确定和缩小最优参数组搜索的方向与规模。同时，交叉复制和信息突变的技术，能有效帮助跳出局部搜索范围，避免落入局部最优情况。最后，多个搜索信息点的同步执行，可高效确定全局最优解，从而获取最优预测模型参数组，获得性能最好的预测模型。

目前，国内已有许多学者将遗传算法优异特性运用于提升各类机器学习的性能，如李响等人结合遗传算法优化SVM的参数，应用在海洋中钢材腐蚀速率预测中，结果表明经GA优化的SVM有更精确的预测结果；李瀚阳等人提出了一种基于GA-BP的手足口病预估模型，利用遗传算法对BP网络的初始权值及阈值进行优化，证明了经优化的BP相比传统BP模型有更准确的手足口病预测精度；雷雪梅等人运用遗传算法对XGBoost进行改进，发现优化的XGBoost在高血压菜谱判定上比传统的XGBoost有更优秀的识别准确性[22]。结合国内利用遗传算改进机器学习模型并取得优异成果的研究现状，本文提出一种基于遗传算法的LightGBM销量预测改进模型GA_LightGBM，将LightGBM参数组的寻优问题看作遗传算法的搜索目标，利用遗传算法GA对LightGBM进行调参优化，解决在对LightGBM调参时出现的因低效率、慢收敛以及局部最优而导致的低准确率的问题，得到LightGBM的无偏差、全局最优参数组，从而提升景区产品销量预估模型的准确性。此外，GA算法的高鲁棒性，对于去除样本噪声的干扰，提高销量估测模型的泛化能力和稳健性也有一定帮助。    

算法设计

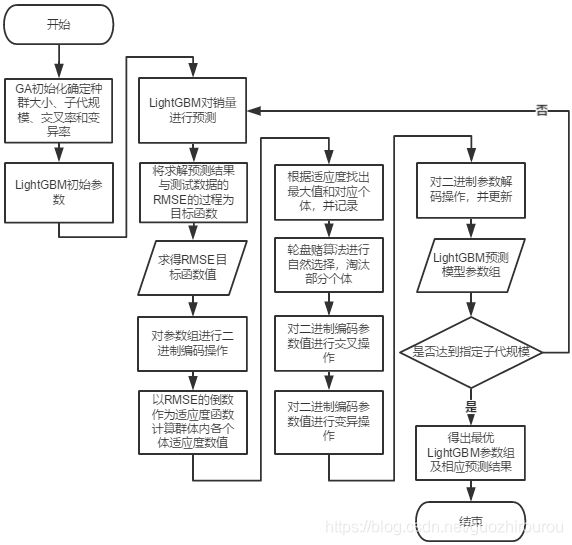
    结合遗传算法基本流程图见图4-3，对LightGBM进行参数优化，设计改进的算法流程如下图4-4所示：

 

基于遗传算法融合的LightGBM改进方案

本改进算法的实现流程为：

（1）初始化GA种群与LightGBM参数

（2）训练LightGBM预测模型，将求解RMSE过程定义为目标函数

（3）求解当前种群各个体的目标函数值，即不同参数组下的LightGBM预测模型的RMSE取值大小

（4）对中群内各个体进行二进制编码，即对每个待寻优参数进行编码

（5）计算种群内各个体的适应度函数值，即目标函数值RMSE的倒数

（6）找出适应度函数值最大时对应的参数组，并记录结果

（7）运用轮盘赌算法进行自然选择，保留被选中的参数组

（8）对剩余参数组按交叉率进行二进制位交换操作

（9）对剩余参数组按变异率进行二进制位变异操作

（10）对记录的适应度最大的二进制参数组进行解码操作，更新当前最优参数组

（11）重复上述（2）~（10）操作，直至子代数量达到初始设定值

（12）输出最优参数组和预测值RMSE表现

代码实现

#coding=utf-8
from __future__ import division
import numpy as np
import pandas as pd
import random
import math
from sklearn import metrics
from sklearn.model_selection import train_test_split
import xgboost as xgb

import lightgbm as lgb
from random import randint
# from xgboost.sklearn import XGBClassifiers
 
 
'''
群体大小，一般取20~100；终止进化代数，一般取100~500；交叉概率，一般取0.4~0.99；变异概率，一般取0.0001~0.1。
'''
# generations = 400   # 繁殖代数 100
pop_size = 500      # 种群数量  500
# max_value = 10      # 基因中允许出现的最大值 （可防止离散变量数目达不到2的幂的情况出现，限制最大值，此处不用） 
chrom_length = 15    # 染色体长度  
pc = 0.6            # 交配概率  
pm = 0.01           # 变异概率  
results = []      # 存储每一代的最优解，N个三元组（auc最高值, n_estimators, max_depth）  
fit_value = []      # 个体适应度  
fit_mean = []       # 平均适应度 
# pop = [[0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0] for i in range(pop_size)] # 初始化种群中所有个体的基因初始序列
 
random_seed = 20
cons_value = 0.19 / 31 # (0.20-0.01）/ (32 - 1)
 
 
 
'''要调试的参数有：（参考：http://xgboost.readthedocs.io/en/latest/parameter.html）
   tree_num：基树的棵数   ----------------（要调的参数）
   eta: 学习率（learning_rate），默认值为0.3，范围[0,1]  ----------------（要调的参数）
   max_depth: 最大树深，默认值为6   ----------------（要调的参数）
   min_child_weight：默认值为1，范围[0, 正无穷]，该参数值越小，越容易 overfitting，当它的值较大时，可以避免模型学习到局部的特殊样本。 ----------（要调的参数）
   gamma：默认值为0，min_split_loss，范围[0, 正无穷]
   subsample：选择数据集百分之多少来训练，可以防止过拟合。默认值1，范围(0, 1]，理想值0.8
   colsample_bytree：subsample ratio of columns when constructing each tree，默认值1，范围(0, 1]，理想值0.8，太小的值会造成欠拟合
   lambda：L2 regularization term on weights, increase this value will make model more conservative.参数值越大，模型越不容易过拟合
   alpha：L1 regularization term on weights, increase this value will make model more conservative.参数值越大，模型越不容易过拟合
   上述参数，要调的有4个，其他的采用理想值就可以
   tree_num: [10、 20、 30、......150、160] 用4位二进制, 0000代表10
   eta: [0.01, 0.02, 0.03, 0.04, 0.05, ...... 0.19, 0.20]   0.2/0.01=20份，用5位二进制表示足够（2的4次方<20<2的5次方）
       00000 -----> 0.01
       11111 -----> 0.20
       0.01 + 对应十进制*（0.20-0.01）/ (2的5次方-1)
   max_depth:[3、4、5、6、7、8、9、10]   用3位二进制
   min_child_weight: [1, 2, 3, 4, 5, 6, 7, 8]  用3位二进制
   示例：   0010,         01001,               010,      110  （共15位）
         tree_num         eta               max_depth  min_child_weight
        (1+2)*10=30  0.01+9*0.005939=0.06       3+2=5      1+6=7
'''
#定义评价函数rmspe    均方根对数误差
def rmspe(y, yhat):
    return np.sqrt(np.mean((yhat/y-1) ** 2))

def xgboostModel(tree_num, eta, max_depth, min_child_weight, random_seed):

    #---------------------------数据准备------------------------
    data = pd.read_csv('UnFeature.csv',low_memory=False)
    #因为销售额为0的记录不计入评分，所以只采用店铺为开，且销售额大于0的数据进行训练
    data = data[data["Open"] != 0]
    data = data[data["Sale"] > 0]

    data = data[:500000]
    
    data.fillna(0, inplace=True)

    #不带特征工程
    data.drop(['Date','Open','PromoInterval','monthStr','Customers'],axis=1,inplace =True)

    #不带特征工程
    
    #data.drop(['Date','Customers','Open','PromoInterval','monthStr'],axis=1,inplace =True)
    target = np.log1p(data.Sale)
    data.drop(['Sale'],axis=1,inplace =True)
    X_train,X_test,y_train,y_test =train_test_split(data,target,test_size=0.2)
    #--------------------------------------------------------------

    # 创建成lgb特征的数据集格式
    lgb_train = lgb.Dataset(X_train, y_train) # 将数据保存到LightGBM二进制文件将使加载更快
    lgb_eval = lgb.Dataset(X_test, y_test, reference=lgb_train)  # 创建验证数据
    params = {
        'task': 'train',
        'boosting_type': 'gbdt',  # 设置提升类型
        'objective': 'regression', # 目标函数
        'early_stopping_rounds': 100,
        'eval_metric': 'rmse',  # 评估函数
        #'num_leaves': 31,   # 叶子节点数
        'learning_rate': eta,  # 学习速率
        'feature_fraction': 0.8, # 建树的特征选择比例
        'bagging_fraction': 0.8, # 建树的样本采样比例
        #'bagging_freq': 5,  # k 意味着每 k 次迭代执行bagging
        'verbose': 1, # <0 显示致命的, =0 显示错误 (警告), >0 显示信息
        'max_depth': max_depth, 
        'min_child_weight': min_child_weight,
        'seed': randint(1,10)
    }
    print('Start training...')
    # 训练 cv and train              
    model = lgb.train(params,lgb_train,num_boost_round=tree_num,valid_sets=lgb_eval) # 训练数据需要参数列表和数据集
    yhat = model.predict(X_test, num_iteration=model.best_iteration)
    error =  rmspe( np.expm1(yhat), np.expm1(y_test))

    return error
 
 
 
def loadFile(filePath):
    fileData = pd.read_csv(filePath)
    return fileData
 
 
# Step 1 : 对参数进行编码（用于初始化基因序列，可以选择初始化基因序列，本函数省略）
def geneEncoding(pop_size, chrom_length):  
    pop = [[]]
    for i in range(pop_size):
        temp = []
        for j in range(chrom_length):
            temp.append(random.randint(0, 1))
        pop.append(temp)
    return pop[1:]
 
# Step 2 : 计算个体的目标函数值
def cal_obj_value(pop):
    objvalue = []
    variable = decodechrom(pop)
    for i in range(len(variable)):
        tempVar = variable[i]
 
        tree_num_value = (tempVar[0] + 1)* 70   #*10
        eta_value = 0.01 + tempVar[1] * cons_value
        max_depth_value = 3 + tempVar[2]
        min_child_weight_value = 1 + tempVar[3]
 
        #aucValue = xgboostModel(tree_num_value, eta_value, max_depth_value, min_child_weight_value, random_seed)
        error = xgboostModel(tree_num_value, eta_value, max_depth_value, min_child_weight_value, random_seed)
       
        #objvalue.append(aucValue)
        objvalue.append(error)
    return objvalue #目标函数值objvalue[m] 与个体基因 pop[m] 对应 
 
 
# 对每个个体进行解码，并拆分成单个变量，返回 tree_num（4）、eta（5）、max_depth（3）、min_child_weight（3）
def decodechrom(pop):
    variable = []
    for i in range(len(pop)):
        res = []
        
        # 计算第一个变量值，即 0101->10(逆转)
        temp1 = pop[i][0:4]
        v1 = 0
        for i1 in range(4):
            v1 += temp1[i1] * (math.pow(2, i1))
        res.append(int(v1))
        
        # 计算第二个变量值
        temp2 = pop[i][4:9]
        v2 = 0
        for i2 in range(5):
            v2 += temp2[i2] * (math.pow(2, i2))
        res.append(int(v2))
 
        # 计算第三个变量值
        temp3 = pop[i][9:12]
        v3 = 0
        for i3 in range(3):
            v3 += temp3[i3] * (math.pow(2, i3))
        res.append(int(v3))
 
        # 计算第四个变量值
        temp4 = pop[i][12:15]
        v4 = 0
        for i4 in range(3):
            v4 += temp4[i4] * (math.pow(2, i4))
        res.append(int(v4))
 
        variable.append(res)
    return variable
 
 
# Step 3: 计算个体的适应值（计算最大值，于是就淘汰负值就好了）
def calfitvalue(obj_value):
    fit_value = []
    temp = 1.0  #0.0
    Cmin = 0
    for i in range(len(obj_value)):
        if(obj_value[i] + Cmin < 1): #>0
            temp = Cmin + obj_value[i]
        else:
            temp = 1.0
        fit_value.append(temp)
    return fit_value
 
 
# Step 4: 找出适应函数值中最大值，和对应的个体
def best(pop, fit_value):
    best_individual = pop[0]
    best_fit = fit_value[0]
    for i in range(1, len(pop)):
        #if(fit_value[i] > best_fit):
        if(fit_value[i] < best_fit):
            best_fit = fit_value[i]
            best_individual = pop[i]
    return [best_individual, best_fit]
 
 
# Step 5: 每次繁殖，将最好的结果记录下来(将二进制转化为十进制)
def b2d(best_individual):
    # 计算第一个变量值
    temp1 = best_individual[0:4]
    v1 = 0
    for i1 in range(4):
        v1 += temp1[i1] * (math.pow(2, i1))
    v1 = (v1 + 1) * 70    #*10
    
    # 计算第二个变量值
    temp2 = best_individual[4:9]
    v2 = 0
    for i2 in range(5):
        v2 += temp2[i2] * (math.pow(2, i2))
    v2 = 0.01 + v2 * cons_value
 
    # 计算第三个变量值
    temp3 = best_individual[9:12]
    v3 = 0
    for i3 in range(3):
        v3 += temp3[i3] * (math.pow(2, i3))
    v3 = 3 + v3
 
    # 计算第四个变量值
    temp4 = best_individual[12:15]
    v4 = 0
    for i4 in range(3):
        v4 += temp4[i4] * (math.pow(2, i4))
    v4 = 1 + v4
 
    return int(v1), float(v2), int(v3), int(v4)
 
 
# Step 6: 自然选择（轮盘赌算法）
def selection(pop, fit_value):
    # 计算每个适应值的概率
    new_fit_value = []
    total_fit = sum(fit_value)
    for i in range(len(fit_value)):
        new_fit_value.append(fit_value[i] / total_fit)
    # 计算每个适应值的累积概率
    cumsum(new_fit_value)
    # 生成随机浮点数序列
    ms = []
    pop_len = len(pop)
    for i in range(pop_len):
        ms.append(random.random())
    # 对生成的随机浮点数序列进行排序
    ms.sort()
    # 轮盘赌算法（选中的个体成为下一轮，没有被选中的直接淘汰，被选中的个体代替）
    fitin = 0
    newin = 0
    newpop = pop
    while newin < pop_len:
        if(ms[newin] < new_fit_value[fitin]):
            newpop[newin] = pop[fitin]
            newin = newin + 1
        else:
            fitin = fitin + 1
    pop = newpop
 
# 求适应值的总和
def sum(fit_value):
    total = 0
    for i in range(len(fit_value)):
        total += fit_value[i]
    return total
 
# 计算累积概率
def cumsum(fit_value):
    temp=[]
    for i in range(len(fit_value)):
        t = 0
        j = 0
        while(j <= i):
            t += fit_value[j]
            j = j + 1
        temp.append(t)
    for i in range(len(fit_value)):
        fit_value[i]=temp[i]
 
# Step 7: 交叉繁殖
def crossover(pop, pc): #个体间交叉，实现基因交换
    poplen = len(pop)
    for i in range(poplen - 1):
        if(random.random() < pc):
            cpoint = random.randint(0,len(pop[0]))
            temp1 = []
            temp2 = []
            temp1.extend(pop[i][0 : cpoint])
            temp1.extend(pop[i+1][cpoint : len(pop[i])])
            temp2.extend(pop[i+1][0 : cpoint])
            temp2.extend(pop[i][cpoint : len(pop[i])])
            pop[i] = temp1
            pop[i+1] = temp2
 
 
# Step 8: 基因突变
def mutation(pop, pm):
    px = len(pop)
    py = len(pop[0])
    for i in range(px):
        if(random.random() < pm):
            mpoint = random.randint(0, py-1)
            if(pop[i][mpoint] == 1):
                pop[i][mpoint] = 0
            else:
                pop[i][mpoint] = 1
 
 
def writeToFile(var, w_path):
    f=open(w_path,"a+")
    for item in var:
        f.write(str(item) + "\r\n")
    f.close()
 
 
def generAlgo(generations):
    pop = geneEncoding(pop_size, chrom_length)
    print(str(generations)+" start...")
    for i in range(generations):
        # print("第 " + str(i) + " 代开始繁殖......")
        obj_value = cal_obj_value(pop) # 计算目标函数值
        # print(obj_value)
        fit_value = calfitvalue(obj_value) #计算个体的适应值
        # print(fit_value)
        [best_individual, best_fit] = best(pop, fit_value) #选出最好的个体和最好的函数值
        # print("best_individual: "+ str(best_individual))
        v1, v2, v3, v4 = b2d(best_individual)
        results.append([best_fit, v1, v2, v3, v4]) #每次繁殖，将最好的结果记录下来
        # print(str(best_individual) + " " + str(best_fit))
        selection(pop, fit_value) #自然选择，淘汰掉一部分适应性低的个体
        crossover(pop, pc) #交叉繁殖
        mutation(pop, pc) #基因突变
    results.sort()

    writeToFile(results, "generation_" + str(generations) + ".txt")
    print(results[-1])
 
 
 
if __name__ == '__main__':
    gen = [100]   #gen = [100, 200, 300, 400, 500]
    for g in gen:
        generAlgo(int(g))

 

 

实验结果与对比

为进一步研究基于遗传算法改进的LightGBM销量预测模型性能，设计两组对照实验：基于网格搜索GridSearch参数优化模型和基于遗传算法GA参数优化模型的对比实验以及基于遗传算法GA优化LightGBM模型对比实验。

GridSearch（网格搜索）调参法是一种常见的调参方法，该方法实质是循环遍历不同参数的候选值，通过模型检测，找出结果最优的参数组合，是一种简单暴力的穷举搜索方法。该方法在参数取值范围足够大且遍历粒度足够小的情况下可以找出全局最优解。但通常参数只在某一较小区间内取值时，预测模型才有较高的准确性，多数情况下，过大的参数寻优范围虽有利于挖掘全局最优解，但其大部分范围区间对于参数取值是不利甚至无用的，会使预测模型表现低效且差劲，造成大量计算资源的浪费。且一旦参数众多，遍历粒度不够细时，GridSearch搜索法仍有可能无法获得最优参数组。相比之下，遗传算法更加智能，适应度函数使搜索过程有明确的目标，使搜索方向总朝着最优化的结果发展。而交叉和变异概率又给搜索过程带来一定随机性，更利于寻求全局最优点，获取最优化性能的预测模型。

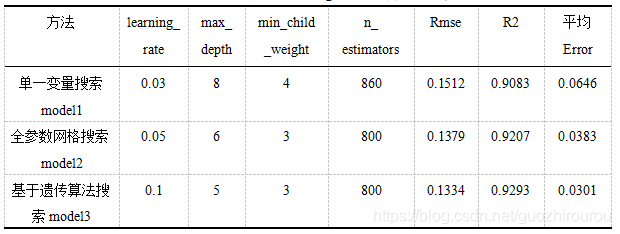
在本对比实验中，依旧对LightGBM影响较大的的四项参数num_boost_round、learning_rate、max_depth和min_child_weight进行讨论，同时加入单一变量调参对比。单一变量调参即保持其他参数不变，每次只改变其中一项参数数值，通过观测LightGBM预测准确性波动情况，确定该参数最终取值，缺点是忽略了组合参数对模型预测结果的影响，很难达到全局最优。

可以看出，由单一变量得到的调参结果最差，模型精度远小于遗传算法调参方式，且相对误差在随机抽取的5组上表现出明显的波动，不及遗传算法优化调参的稳定；而网格调参结果已经较为接近遗传算法调参结果，在5组数据表现出一致的预测趋势，相对误差的震荡范围也更为稳定，但其平均相对误差、R2仍小于遗传算法调参方式，RMSE仍大于遗传算法调参方式，说明经遗传算法优化调参的LightGBM预测模型相对于网格调参、单一变量调参模型有更好的准确性和拟合性。