Transformer模型梳理

本文是对Transformer模型的梳理文章，主要学习资料为知乎的一篇文章 和一篇博客。初学transformer，有讲的不对的地方，可以评论区评论告诉我，我会及时改正的。

1 Transformer整体结构

Transformer的整体结构如下图所示：

上图展示的是用于机器翻译的Transformer，Transformer的整体结构分为两部分，分别是Encoder部分和Decoder部分，图中的Encoder和Decoder都包含6个block。Transformer模型的运行流程如下所示：

第一步： 输入部分，获取输入句子的每个单词的表示向量x，表示向量x由单词的Embedding(Embedding就是从原始数据提取出来的特征)和单词位置的Embedding相加得到

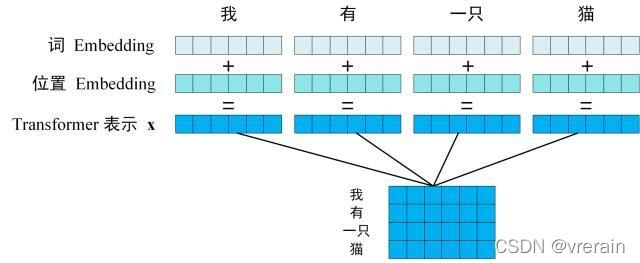
第二步： 将得到的单词表示向量矩阵 (如上图所示，每一行是一个单词的表示 x) 传入 Encoder 中，经过 6 个 Encoder block 后可以得到句子所有单词的编码信息矩阵 C，如下图。单词向量矩阵用 $X_{n\times d}$ 表示， n 是句子中单词个数，d 是表示向量的维度 (论文中 d=512)。每一个 Encoder block 输出的矩阵维度与输入完全一致

第三步： 将 Encoder 输出的编码信息矩阵 C传递到 Decoder 中，Decoder 依次会根据当前翻译过的单词 1~ i 翻译下一个单词 i+1，如下图所示。在使用的过程中，翻译到单词 i+1 的时候需要通过 Mask (掩盖) 操作遮盖住 i+1 之后的单词。

上面Decoder接收了Encoder的编码矩阵C，然后结合“"预测出I,然后又结合“"和"I"预测出have。以此类推。

2 Transformer的输入

Transformer 中单词的输入表示 x由单词 Embedding 和位置 Embedding （Positional Encoding）相加得到。

单词Embedding

有很多种，例如word2vec、Glove等预训练算法。

位置Embedding

因为Transformer不采用RNN结构，只能使用全局信息，不能利用单词的输入顺序，而这部分信息对于NLP来说是十分重要的，所以利用位置Embedding来保存单词的相对位置和绝对位置信息。

位置 Embedding 用 PE表示，PE 的维度与单词 Embedding 是一样的。PE 可以通过训练得到，也可以使用某种公式计算得到。在 Transformer 中采用了后者，计算公式如下：

其中，pos 表示单词在句子中的位置，d 表示 PE的维度 (与词 Embedding 一样)，2i 表示偶数的维度，2i+1 表示奇数维度 (即 2i≤d, 2i+1≤d)。使用这种公式计算 PE 有以下的好处：

• 使 PE 能够适应比训练集里面所有句子更长的句子，假设训练集里面最长的句子是有 20 个单词，突然来了一个长度为 21的句子，则使用公式计算的方法可以计算出第 21 位的 Embedding。
• 可以让模型容易地计算出相对位置，对于固定长度的间距k，PE(pos+k) 可以用 PE(pos) 计算得到。因为 Sin(A+B) = Sin(A)Cos(B) + Cos(A)Sin(B), Cos(A+B) = Cos(A)Cos(B) - Sin(A)Sin(B)。 将单词的词 Embedding和位置 Embedding 相加，就可以得到单词的表示向量 x，x 就是 Transformer 的输入。

3 Self-Attentin(自注意力机制)

上图是论文中 Transformer 的内部结构图，左侧为 Encoder block，右侧为 Decoder block。红色圈中的部分为 Multi-Head Attention，是由多个 Self-Attention组成的，可以看到 Encoder block 包含一个 Multi-Head Attention，而 Decoder block 包含两个 Multi-Head Attention (其中有一个用到 Masked)。Multi-Head Attention 上方还包括一个 Add & Norm 层，Add 表示残差连接 (Residual Connection) 用于防止网络退化，Norm 表示 Layer Normalization，用于对每一层的激活值进行归一化。

Self-Attention结构

上图是Self-Attention的结构，在计算的时候需要用到矩阵Q(查询),K(键值),V(值)。在实际中，Self-Attention 接收的是输入(单词的表示向量x组成的矩阵X) 或者上一个 Encoder block 的输出。而Q,K,V正是通过 Self-Attention 的输入进行线性变换得到的，另外需要注意的是Q,K,V的维度需要小于输入向量(即单词的表示向量X)的维度。

Q、K、V的计算

Self-Attention 的输入用矩阵X进行表示，则可以使用线性变阵矩阵WQ,WK,WV计算得到Q,K,V。计算如下图所示，注意 X, Q, K, V 的每一行都表示一个单词。

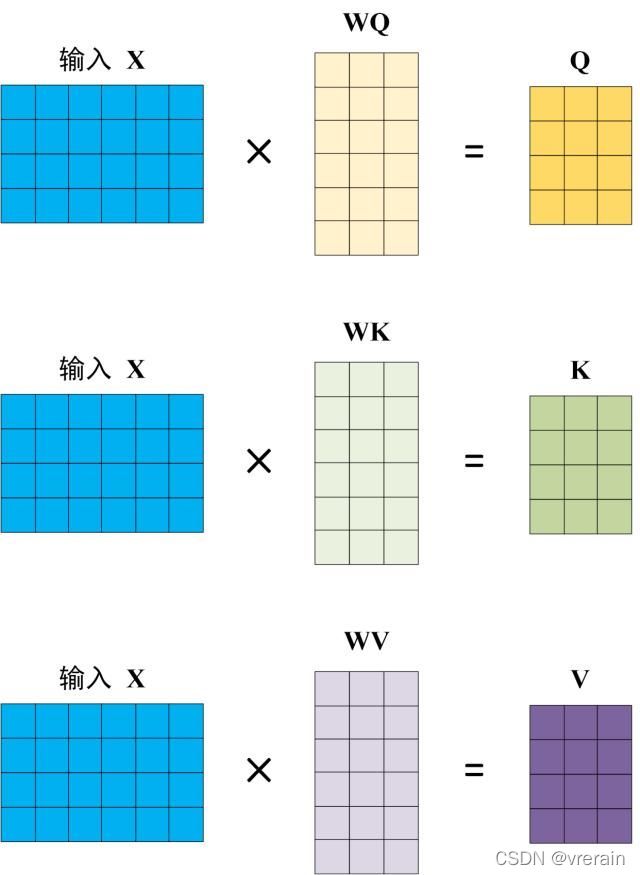
Self-Attention的输出

得到矩阵 Q, K, V之后就可以计算出 Self-Attention 的输出了，计算的公式如下：

公式中计算矩阵Q和K每一行向量的内积，为了防止内积过大，因此除以 $d_k$的平方根。Q乘以K的转置后，得到的矩阵行列数都为 n，n 为句子单词数，这个矩阵可以表示单词之间的 attention 强度。下图为Q乘以$K^T$，1234 表示的是句子中的单词。

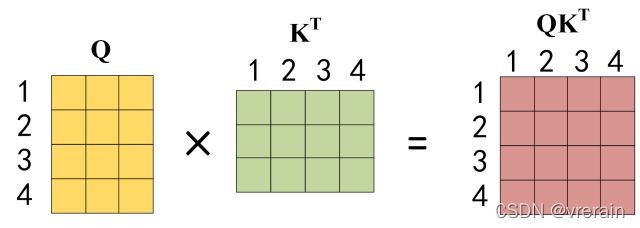
得到$Q{K}^T$之后，使用 Softmax 计算每一个单词对于其他单词的 attention 系数，公式中的 Softmax 是对矩阵的每一行进行 Softmax，即每一行的和都变为 1。

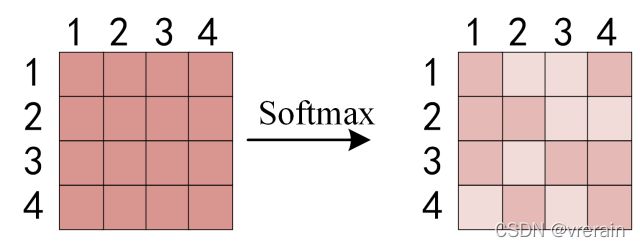
得到 Softmax 矩阵之后可以和V相乘，得到最终的输出Z，也就是Self-Attention的输出。

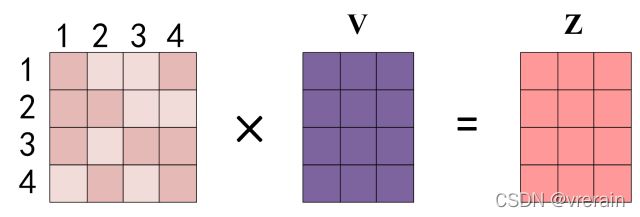
上图中 Softmax 矩阵的第 1 行表示单词 1 与其他所有单词的 attention 系数，最终单词 1 的输出 $Z_1$ 等于所有单词 i 的值 $V_i$根据 attention 系数的比例加在一起得到，如下图所示：

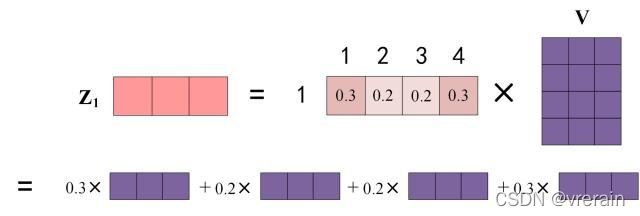
总体流程如下图所示：

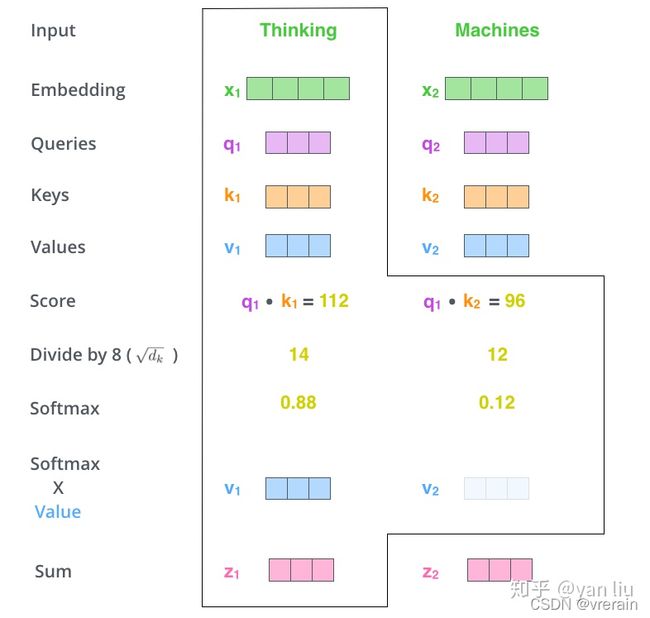
Query，Key，Value的概念取自于信息检索系统，举个简单的搜索的例子来说。当你在某电商平台搜索某件商品（年轻女士冬季穿的红色薄款羽绒服）时，你在搜索引擎上输入的内容便是Query，然后搜索引擎根据Query为你匹配Key（例如商品的种类，颜色，描述等），然后根据Query和Key的相似度得到匹配的内容（Value)。

self-attention中的Q，K，V也是起着类似的作用，在矩阵计算中，点积是计算两个矩阵相似度的方法之一，因此式1中使用了$Q{K}^T$进行相似度的计算。接着便是根据相似度进行输出的匹配，这里使用了加权匹配的方式，而权值就是query与key的相似度。

Multi-Head Attention

在上一步，我们已经知道怎么通过 Self-Attention 计算得到输出矩阵 Z，而 Multi-Head Attention 是由多个 Self-Attention 组合形成的，下图是论文中 Multi-Head Attention 的结构图。

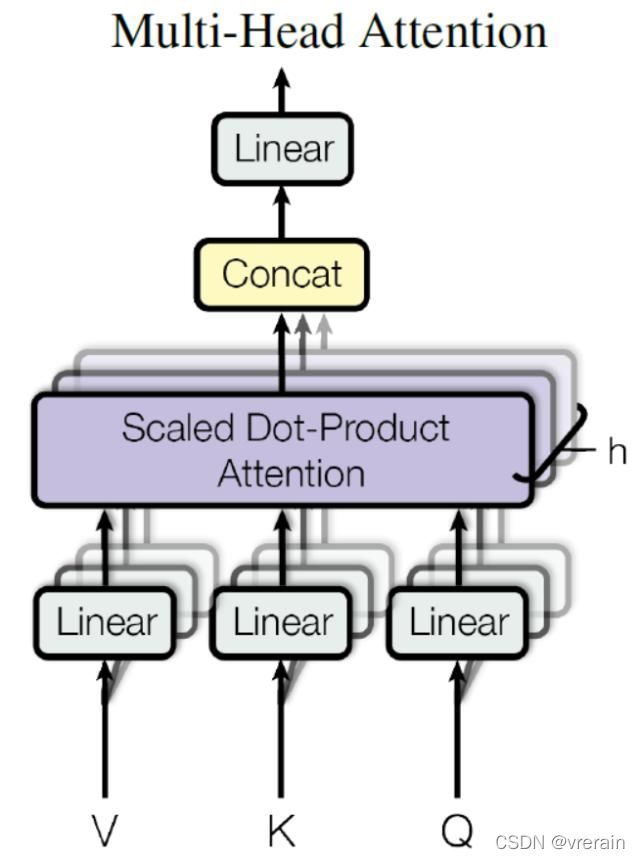
从上图可以看到 Multi-Head Attention 包含多个 Self-Attention 层，首先将输入X分别传递到 h 个不同的 Self-Attention 中，计算得到 h 个输出矩阵Z。下图是 h=8 时候的情况，此时会得到 8 个输出矩阵Z。

得到 8 个输出矩阵 Z1 到 Z8 之后，Multi-Head Attention 将它们拼接在一起 (Concat)，然后传入一个Linear层，得到 Multi-Head Attention 最终的输出Z。

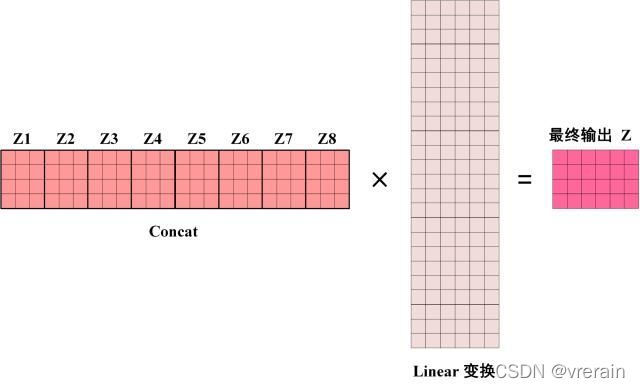
可以看到 Multi-Head Attention 输出的矩阵Z与其输入的矩阵X的维度是一样的。

4 Encoder结构

上图红色部分是 Transformer 的 Encoder block 结构，可以看到是由 Multi-Head Attention, Add & Norm, Feed Forward, Add & Norm 组成的。刚刚已经了解了 Multi-Head Attention 的计算过程，现在了解一下 Add & Norm 和 Feed Forward 部分。

Add & Norm

Add & Norm 层由 Add 和 Norm 两部分组成，其计算公式如下：

其中 X表示 Multi-Head Attention 或者 Feed Forward 的输入(从结构图中可以看出，X输入到这两个地方)，MultiHeadAttention(X) 和 FeedForward(X) 表示输出 (输出与输入 X 维度是一样的，所以可以相加)。

Add指 X+MultiHeadAttention(X)，是一种残差连接，通常用于解决多层网络训练的问题，可以让网络只关注当前差异的部分，在 ResNet 中经常用到：

Norm指 Layer Normalization，通常用于 RNN 结构，Layer Normalization 会将每一层神经元的输入都转成均值方差都一样的，这样可以加快收敛。

Feed Forward

Feed Forward层比较简单，是一个两层的全连接层，第一层的激活函数是ReLU，第二层是一个线性激活函数，可以表示为：

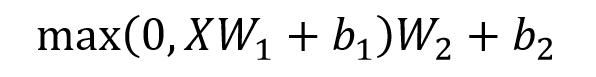
X是输入，Feed Forward 最终得到的输出矩阵的维度与X一致。
整体流程如下所示：

组成Encoder

通过上面描述的 Multi-Head Attention, Feed Forward, Add & Norm 就可以构造出一个 Encoder block，Encoder block 接收输入矩阵 $X_{(n\times d)}$，并输出一个矩阵 $O_{(n\times d)}$ 。通过多个 Encoder block 叠加就可以组成 Encoder。

第一个 Encoder block 的输入为句子单词的表示向量矩阵，后续 Encoder block 的输入是前一个 Encoder block 的输出，最后一个 Encoder block 输出的矩阵就是编码信息矩阵 C，这一矩阵后续会用到 Decoder 中。

5 Decoder结构

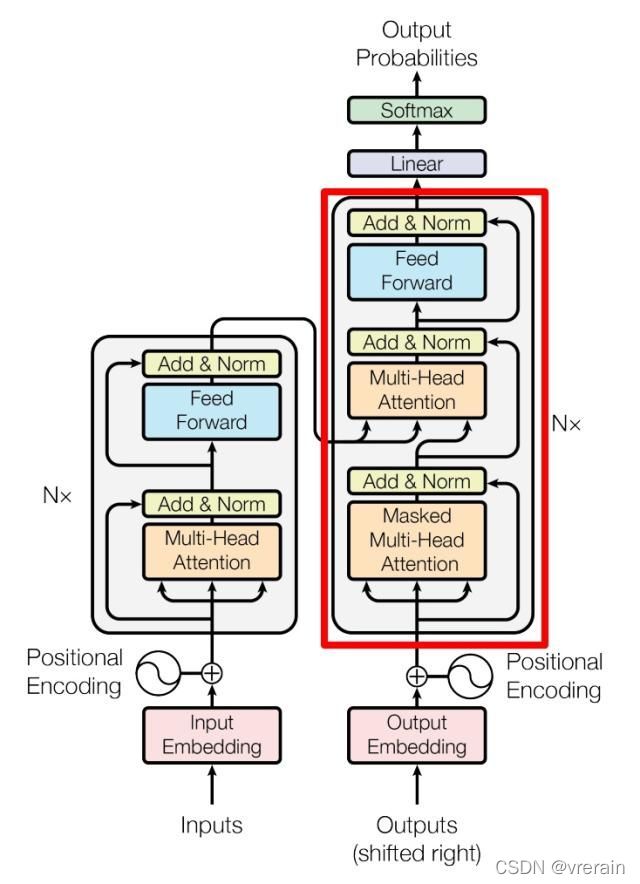
上图红色部分为 Transformer 的 Decoder block 结构，与 Encoder block 相似，但是存在一些区别：

• 包含两个 Multi-Head Attention 层。
• 第一个 Multi-Head Attention 层采用了 Masked 操作。
• 第二个 Multi-Head Attention 层的K, V矩阵使用 Encoder 的编码信息矩阵C进行计算，而Q使用上一个Decoder block 的输出计算。
• 最后有一个 Softmax 层计算下一个翻译单词的概率。

第一个Multi-Head Attention

Decoder block 的第一个 Multi-Head Attention 采用了 Masked 操作，因为在翻译的过程中是顺序翻译的，即翻译完第 i 个单词，才可以翻译第 i+1 个单词。通过 Masked 操作可以防止第 i 个单词知道 i+1 个单词之后的信息。下面以 “我有一只猫” 翻译成 “I have a cat” 为例，了解一下 Masked 操作。

下面的描述中使用了类似 Teacher Forcing 的概念，不熟悉 Teacher Forcing 的童鞋可以参考以下上一篇文章Seq2Seq 模型详解。在 Decoder 的时候，是需要根据之前的翻译，求解当前最有可能的翻译，如下图所示。首先根据输入 “” 预测出第一个单词为 “I”，然后根据输入 " I" 预测下一个单词 “have”。

Decoder 可以在训练的过程中使用 Teacher Forcing 并且并行化训练，即将正确的单词序列 ( I have a cat) 和对应输出 (I have a cat ) 传递到 Decoder。那么在预测第 i 个输出时，就要将第 i+1 之后的单词掩盖住，注意 Mask 操作是在 Self-Attention 的 Softmax 之前使用的，下面用 0 1 2 3 4 5 分别表示 " I have a cat "。

第一步： 是 Decoder 的输入矩阵和 Mask 矩阵，输入矩阵包含 " I have a cat" (0, 1, 2, 3, 4) 五个单词的表示向量，Mask 是一个 5×5 的矩阵。在 Mask 可以发现单词 0 只能使用单词 0 的信息，而单词 1 可以使用单词 0, 1 的信息，即只能使用之前的信息。

第二步：接下来的操作和之前的 Self-Attention 一样，通过输入矩阵X计算得到Q,K,V矩阵。然后计算Q和 $K^T$ 的乘积$Q{K}^T$ 。

第三步： 在得到 $Q{K}^T$之后需要进行 Softmax，计算 attention score，我们在 Softmax 之前需要使用Mask矩阵遮挡住每一个单词之后的信息，遮挡操作如下：

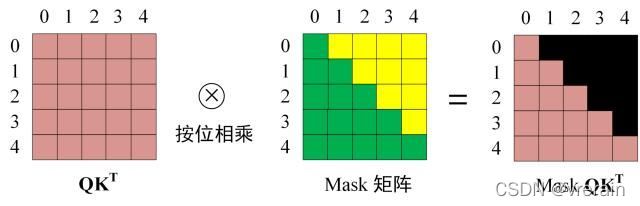
得到 Mask $Q{K}^T$ 之后在 Mask $Q{K}^T$上进行 Softmax，每一行的和都为 1。但是单词 0 在单词 1, 2, 3, 4 上的 attention score 都为 0。

第四步： 使用 Mask $Q{K}^T$与矩阵 V相乘，得到输出 Z，则单词 1 的输出向量 $Z_1$是只包含单词 1 信息的。

第五步： 通过上述步骤就可以得到一个 Mask Self-Attention 的输出矩阵 $Z_i$，然后和 Encoder 类似，通过 Multi-Head Attention 拼接多个输出$Z_i$ 然后计算得到第一个 Multi-Head Attention 的输出Z，Z与输入X维度一样。

第二个Multi-Head Attention

Decoder block 第二个 Multi-Head Attention 变化不大， 主要的区别在于其中 Self-Attention 的 K, V矩阵不是使用 上一个 Decoder block 的输出计算的，而是使用 Encoder 的编码信息矩阵 C 计算的。

根据 Encoder 的输出 C计算得到 K, V，根据上一个 Decoder block 的输出 Z 计算 Q (如果是第一个 Decoder block 则使用输入矩阵 X 进行计算)，后续的计算方法与之前描述的一致。

这样做的好处是在 Decoder 的时候，每一位单词都可以利用到 Encoder 所有单词的信息 (这些信息无需 Mask)。

Softmax预测输出单词

Decoder block 最后的部分是利用 Softmax 预测下一个单词，在之前的网络层我们可以得到一个最终的输出 Z，因为 Mask 的存在，使得单词 0 的输出 Z0 只包含单词 0 的信息，如下：

Softmax 根据输出矩阵的每一行预测下一个单词：

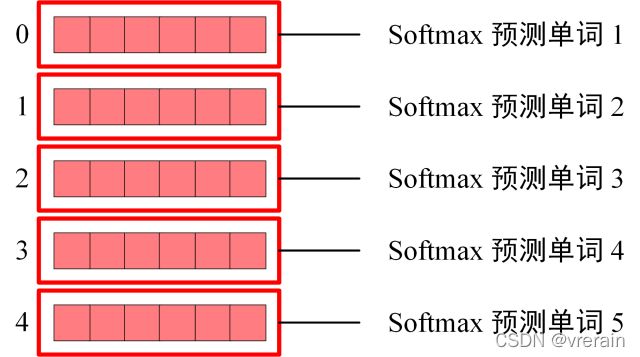
这就是 Decoder block 的定义，与 Encoder 一样，Decoder 是由多个 Decoder block 组合而成。

过程动态演示

对于teacher force，在其他seq2seq模型中也有应用。它是指在每一轮预测时，不使用上一轮预测的输出，而强制使用正确的单词。还以上面这个例子来说，第二轮时，给解码器模块输入“ I” 和 编码器的输出结果，解码器没有正确预测出“Iove”，而是得到了“want”。如果没有采用teacher force，在第三轮时，解码器模块输入的就是“ I want”。如果采用了 teacher force，第三轮时，解码器模块输入的仍然是“ I love”。通过这样的方法可以有效的避免因中间预测错误而对后续序列的预测，从而加快训练速度。而Transformer采用这个方法，为并行化训练提供了可能，因为每个时刻的输入不再依赖上一时刻的输出，而是依赖正确的样本，而正确的样本在训练集中已经全量提供了。值得注意的一点是：Decoder的并行化仅在训练阶段，在测试阶段，因为我们没有正确的目标语句，t时刻的输入必然依赖t-1时刻的输出，这时跟之前的seq2seq就没什么区别了。

6 Transformer 总结

• Transformer 与 RNN 不同，可以比较好地并行训练。 (关于transformer的并行性，这里推荐一篇博客)
• Transformer本身是不能利用单词的顺序信息的，因此需要在输入中添加位置 Embedding，否则 Transformer 就是一个词袋模型了。
• Transformer 的重点是 Self-Attention 结构，其中用到的 Q, K, V矩阵通过输出进行线性变换得到。
• Transformer 中 Multi-Head Attention 中有多个Self-Attention，可以捕获单词之间多种维度上的相关系数 attention score。