【花书笔记|PyTorch版】手动学深度学习301：线性神经网络（理论部分）

3 线性神经网络（上）：理论知识

# 2022.10.5
包括3.1、3.4部分内容

3.1 线性回归

---

特别说明：标识习惯与别书习惯正好相反

• 第i个样本:$x^{(i)}$
• 第i个样本第j个特征:$x_j^{(i)}$

---

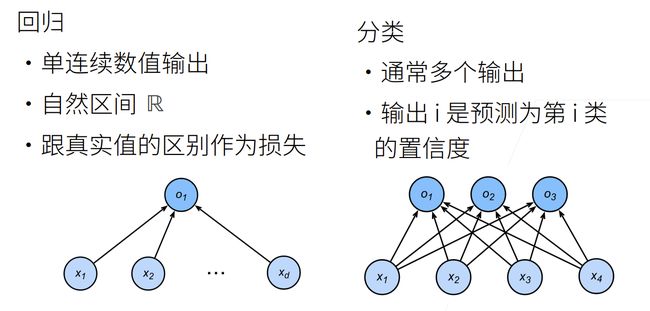
回归（regression）是能为一个或多个自变量与因变量之间关系建模的一类方法。

在机器学习领域中的大多数任务通常都与预测（prediction）有关。 当我们想预测一个数值时，就会涉及到回归问题

3.1.1 线性模型

这里李沐老师标识没有统一，我做了修改

① 一个数据集：
$$\hat{y}=w^{T}x+b$$
即，
$$\hat{y}=w_1{x}_1+...+w_d{x}_d+b$$

• 这里面d为特征 ，$x=[x_1,...,x_d{]}^T:d\times 1$
• w形式与x相同：$w=[w_1,...,w_d{]}^T:d\times 1$

② n个数据集:

$$\hat{y}=Xw+b$$

• $X=[x^{(1)},x^{(2)},...,x^{(n)}{]}^T:n\times d$
• $w:d\times 1$
• $y:n\times 1$

3.1.2 损失函数

损失函数（loss function）能够量化目标的实际值与预测值之间的差距。

通常我们会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。

其中，最常用之一是平方误差作为损失函数：

第i个数据：
$$l^{(i)}(w,b)=\frac{1}{2}({\hat{y}}^{(i)}-y^{(i)}{)}^2$$

我们要的是n个数据预测值都与真实值接近，那么就用期望：

$$L(w,b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}({\hat{y}}^{(i)}-y^{(i)}{)}^2$$

我们要L(w,b)最小时的参数：w,b

$$w^{\ast },b^{\ast }=argmi{n}_{w,b}L(w,b)$$

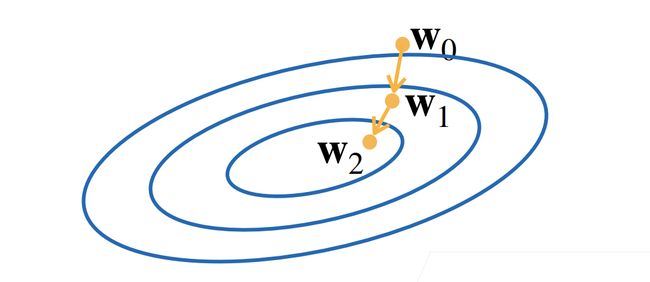
3.1.3 梯度下降

我们怎么去找到这个最小时的w,b呢？- 用梯度下降的方法

1. 挑选一个初始值w0
2. 重复迭代 t=1,2,3…

$$w_t=w_{t-1}-\eta \frac{\partial L}{\partial w_{t-1}}$$

• $\eta :$学习率，步长的超参数

• 学习率要适中，过小收敛太慢，过大可能错过最低点。

3.1.2 矢量化加速

用了一个实例 来证明了 矢量化效率高，所以要矢量化

3.1.3 正态分布与平方损失

其实就是 介绍了一下正态分布 和 最大似然估计 为后面例子铺垫了一下

---

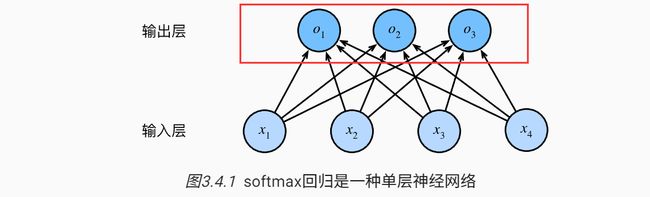
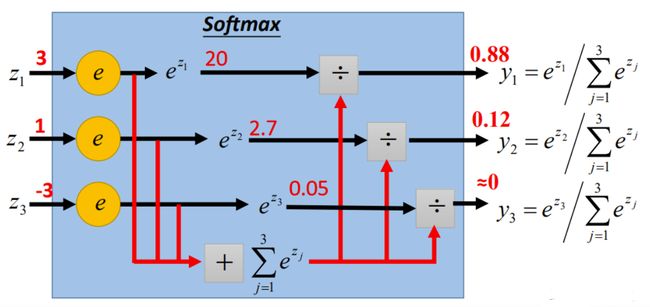
3.4 softmax回归

softmax回归其实是解决离散问题：分类问题

从输出上来看差异：

3.4.4 softmax运算

它主要用在神经网络的最后一层，决定输出的样子

操作就是;每个输出进行了一个类似于求概率 占比的操作:

$${\hat{y}}_j=\frac{exp(o_j)}{{\sum }_{k=1}^{n}exp(o_k)}$$

• 有n个输出$o_1,o_2...，o_n$
• exp(oj) 就是 $e^{o_j}$

就看哪个占比重大，占比重大的 就是要输出的那个类j。 数学表达：

$$\hat{y}=argma{x}_j({\hat{y}}_j)$$

为什么要做这个运算？

解决了 两个问题：将输出值变成了正值且和为1的概率分布。

不做这个操作，一方面 输出层范围不确定，另外 比如输出是猫的值为-1 我们没法直观感知；不方便

3.4.5 小批量样本的矢量化

这个做法是提高计算效率:

• 我们有10000个数据，每个数据10个参数，【传统梯度下降】那么我们每走一步 要计算10万次。通常数据量很大，传统方法通常很难完成这样的时间代价
• 我们通常采用：小批量随机下降法

也就是在兼顾效率的同时，尽量不错过最优解。
小批量是提高效率，随机是为了不错过最优解。

3.4.6 损失函数

3.4.6.1 对数似然

讲的其实就是 条件概率函数 与 损失函数 联系了起来

1.2 ： https://zhuanlan.zhihu.com/p/562681789

3.4.6.3. 交叉熵损失

是分类问题最常用的损失

相对熵的理解：https://blog.csdn.net/wistonty11/article/details/120416080

为什么在逻辑回归中经常用交叉熵 而不是 最小二乘法？

李宏毅老师的解释【见5.3】：https://blog.csdn.net/wistonty11/article/details/120404166