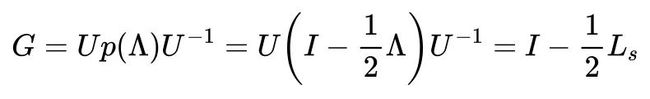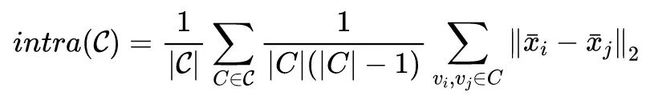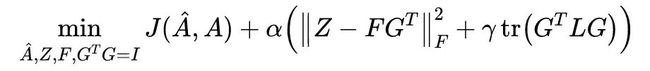图神经网络时代的深度聚类

©PaperWeekly 原创 · 作者｜纪厚业

学校｜北京邮电大学博士生

研究方向｜图神经网络和推荐系统

聚类作为经典的无监督学习算法在数据挖掘/机器学习的发展历史中留下了不可磨灭的印记。其中，经典的聚类算法 K-Means 也被选为数据挖掘十大经典算法。随着深度学习的兴起，一些工作尝试将深度学习技术（如 Autoencoder ）引入到传统聚类算法中，也取得了不错的效果。

近些年，图神经网络已经成为深度学习领域最热门的方向之一， 也在推荐/自然语言处理/计算机视觉等很多领域得到了广泛的应用。

那么，能不能利用图神经网络强大的结构捕获能力来提升聚类算法的效果呢？本文梳理总结了图神经网络赋能的深度聚类算法，供大家参考。

IJCAI 2019

论文标题：Attributed Graph Clustering: A Deep Attentional Embedding Approach

论文来源：IJCAI 2019

论文链接：https://arxiv.org/abs/1906.06532

1.1 论文动机

本文认为之前的深度聚类算法都是 two-step 的：首先学习数据的特征表示 embedding，然后基于特征表示进行数据聚类。这样所学习的数据 embedding 并不是任务导向的。那么，如果能够在学习 embedding 的过程中，针对聚类任务做一些针对性的设计，那么学习到的 embedding 自然可以实现更好的聚类。

针对上述问题，本文提出了一种聚类导向的深度算法 Deep Attentional Embedded Graph Clustering (DAEGC)。DAEGC 一边通过图神经网络来学习节点表示，一边通过一种自训练的图聚类增强同一簇节点之间的内聚性。

下图清晰的展示 two-step 和本文所提出的 DAEGC 的差异。

1.2 模型介绍

下图展示了 DAEGC 的模型框架：

可以看出，整个 DAEGC 主要包含两大模块：带有注意力机制的图自编码器+自训练聚类。

1.3 带有注意力机制的图自编码器

这里就是经典的 GAE 架构：通过对邻居的聚合来学习节点表示，然后利用节点对的内积来重构原始网络结构。比较有特色的部分就是结合注意力机制来学习邻居的权重， 这样可以更好的学习节点表示。

下式展示了融合注意力机制的 GAE 是如何聚合邻居信息来更新节点表示的。本质上就是对邻居的加权平均。

其中， ， 分别是聚合邻居信息前后的节点 的表示，  代表节点  的邻居集合，  表示了节点对 (i, j) 之间的注意力权重。

有了节点表示后， GAE 可以通过计算节点对的内积来重构原始网络结构，进而实现无监督的节点表示学习。

其中， 可以理解为节点对 (i, j) 间存在边的概率。最后，通过经典的 AE 重构损失 就可以对 GAE 进行训练。

1.4 自训练聚类

GAE 所学习到的节点表示只是为了更好的重构网络结构，和聚类并没有直接联系。自训练聚类模块就是对 GAE 所学习到的 embedding 进行约束和整合，使其更适合于聚类任务。假定聚类中为  ， 那么节点  属于某个类别的概率  ， 如下式所示：

这里，  可以看作是节点的分配的分布。进一步的， 为了引入聚类信息来实现聚类导向的节点表示， 我们需要迫使每个节点与相应的聚类中心更近一些，以实现所谓的类内距离最小，类间距离最大。因此，我们定义了如下的目标分布：

在目标分布中， 通过二次方  可以实现一种"强调"的效果（二次方后， 分布会变得更加尖锐，也更置信）。在训练过程中，分布  实际起到了一种标签的效果。最后，通过计算两个分布之间的 KL 散度，来实现互相约束，也就是所谓的自训练。

综合起来，模型最终的损失函数为：

节点  的所处于的簇  （也可以理解为其标签）可以通过下式计算：

1.5 论文实验

作者在 3 个数据集上进行了实现， DAEGC 在大部分情况下都取得了最好的效果。

WWW 2020

论文标题：Structural Deep Clustering Network

论文来源：WWW 2020

论文链接：https://arxiv.org/abs/2002.01633

代码链接：https://github.com/461054993/SDCN

2.1 论文动机

深度自编码器可以通过多层非线性编码来提取特征信息，而图神经网络可以聚合邻居信息来充分挖掘结构信息。为了同时实现对特征的降维抽取和对结构信息的挖掘， 本文提出了 Structural Deep Clustering Network （SDCN）。

通过堆叠多层 GNN， SDCN 实现了对高阶结构信息的捕获。同时，受益于自编码器和 GNN 的自监督， 这里的多层 GNN 并不会出现所谓的过平滑现象。过平滑现象指的是，随着层数的增加，GNN 所学习到的节点表示逐渐变得不可区分。

2.2 模型介绍

在开始介绍模型之前，需要说明的是：如果数据集本身并没有图结构，作者将会通过计算节点之间的 Top-K 相似性利用 KNN 手动构建一张图。下面是两种相似性计算方法：Heat Kernel 和 Dotp roduct。

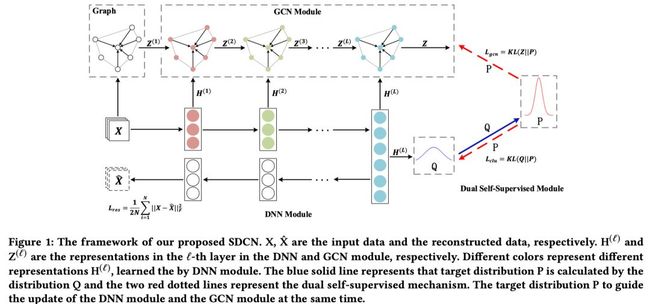
下图展示了整个 SDCN 的模型架构图。可以看出，整个模型主要包含 3 个部分：GCN 模块，DNN 模块和双重自监督模块。

2.3 DNN模块

这里是一个经典的自编码器。编码器将输入  （也就是   ）通过神经网络编码为隐表示  ；解码器将隐表示  解码为  （也就是  ）。

可以看出，通过重构 loss 和多层非线性映射，  可以较好的反映节点的特征信息。

2.4 GCN模块

另一方面， GCN 可以聚合邻居信息来更新节点表示，其更新过程如下：

其中，  是第  层 GCN 学习到的表示，  是带有自联的邻接矩阵，  。

截止到目前为止都是一些常规的 DNN 和 GCN。接下来就是 SDCN 的特色部分：第  层最终表示   实际上混合了初始 GCN 表示   和 DNN 的编码表示  。

可以看出，在这一步，作者将 GNN 和 DNN 联系了起来。第 L 层的最终表示可以进一步映射为一个类别概率，

其中，  可以看做是节点  属于类别  的概率， 其实是一个指示了节点处于不同类别的概率分布。

2.5 双重自监督模块

最后是一个双重自监督模块，其作用体现在两个方面：（1）通过 GCN 部分和 DNN 部分的互相监督可以实现模型的无监督学习。（2）通过引入聚类信息来更好的学习任务导向的节点表示。

与上一篇 19 IJCAI Attributed Graph Clustering：A Deep Attentional Embedding Approach 类似， SDCN 也设计了两个分布。这里不再赘述，详见上一篇的解读。

节点的类别分布为：

目标分布为：

同样的，也是最小化两个分布之间的 KL 散度：

这里，我们可以将  视为标签来对 GCN 模块进行监督。

总的来说， 分布  起到了一个桥接的作用，将 DNN 所学到的表示和 GCN 所学习到的表示进行约束。

模型完整损失函数如下：

节点  的标签可以通过下式计算：

2.6 论文实验

作者在 6 个数据集上做了大量的有效性实验。可以看出， SDCN 在所有数据集上都取得了大幅的提升。

比较有意思的实验是模型层数实验，如下图所示。可以看出，随着层数的增加，模型的效果会有大幅度的提升，并没有出现过平滑现象。

除此之外，作者还测试了不同的混合系数  对模型效果的影响。

IJCAI 2019

论文标题：Attributed Graph Clustering via Adaptive Graph Convolution

论文来源：IJCAI 2019

论文链接：https://arxiv.org/abs/1906.01210

3.1 论文动机

与上一篇 SDCN 相似，本文也利用了高阶结构信息（多层 GNN）来提升聚类的效果。尽管这两篇非常相似，它们也是有一些差异的：1） 本文所提出的AGC是从图信号处理谱图理论的角度来理解 GNN 并增强了聚类效果；2） 本文所涉及的 AGC 可以自适应的选择高阶信息的阶数，而  SDCN 则需要手动指定超参数。

3.2 模型介绍

3.2.1 谱域的图卷积

这里首先简单回顾一下谱域的图卷积：

其中，p(Λ) 是一个频响函数，可以对  中的值（也就是特征值）进行放缩，  ， 分别是经过图滤波器  卷积前后的图信号。

这里，  可以看做一组基信号的加权， 而这组基是由拉普拉斯矩阵  分解得到的，

其中，  ， ， 代表  个基向量， ， ， 是一个对角阵， 的大小可以反映基向量  的平滑程度。

为什么这里需要涉及到“平滑”这个概念呢？图上的“平滑”程度反映了相邻节点的相似程度。图上的高频意味着不平滑，特征值大; 图上的低频意味着平滑，特征值小。

那么在一组基中， 相对平滑的图信号实际上是有利于聚类的。因为聚类的目的是把相似的节点放到一起。

如何实现对低频信号的筛选（也就是对高频信号的抑制）呢？其实很简单，我们只要想办法将较大特征进行压缩。回想上面的频响函数  （ ） 的作用， 我们可以设计恰当的  来实现我们的目的：

很明显，  越大，  越小。相应的图滤波  可以写作：

一阶图卷积可以写作：

那么，k 阶图卷积也呼之欲出，

到这里，也就可以聚合 k 阶邻居来学习节点表示了，也就是所谓的 k 阶图卷积。同时注意，卷积过程中抑制了高频信号，更多的低频信号（更符合聚类要求）被捕获了。

3.2.2 自适应k选择

现在还剩一个问题需要解决，图卷积的 k 阶该如何确定？

这里作者用了一个启发式的方法：逐渐增加 k， 当类内距离开始变小时，停止搜索。内类距离如下所示：

可以看出，这里 k 的选择也是比较符合聚类的要求（类内距离最小，类间距离最大）。

3.3 论文实验

作者在 4 个经典数据集上进行了实验。总的来说，AGC 的效果还是不错的。

arXiv 2020

论文标题：Embedding Graph Auto-Encoder with Joint Clustering via Adjacency Sharing

论文来源：arXiv 2020

论文链接：https://arxiv.org/abs/2002.08643

4.1 论文动机

本文与之前几篇的类似，也是用 GNN 来学习适合于聚类任务的节点表示。比较特别的是，本文同时考虑了 K-Mean 聚类和谱聚类来实现更好的聚类。

4.2 模型介绍

下图展示了本文所提出的 Embedding Graph Auto-Encoder with JOint Clustering via Adjacency Sharing (EGAE-JOCAS) 的整体框架。

4.2.1 图自编码器

首先，作者利用图卷积神经网络来学习节点的表示  ， 然后利用节点表示来尝试重构原始图结构。

略有不同的是，作者这里对  做了一个非线性变换。

作者认为  （函数曲线见下图）可以更好的对节点对的内积进行映射。在  较大的时候，  可以更好的逼近  。

4.2.2 联合聚类

联合聚类的公式如下图所示：

第一项是 K-Mean 聚类，其中 是一个指示器， 实际上反映了节点属于不同簇的概率。

第二项是谱聚类，直观的理解就是，相近的节点应该属于相同的簇。回顾上一篇的"平滑程度"，可以发现它们有异曲同工之妙。

联合之前 GAE 的重构损失，EGAE-JOCAS 最终的目标函数为：

4.3 论文实验

最后，作者在四个数据集上进行了实验。总的来说，EGAE-JOCAS 在所有数据集上都取得了明显的提升。

总结

聚类是机器学习/数据挖掘的一个基础性问题。从传统聚类到深度聚类以及现在图神经网络赋能的聚类， 各种各样的聚类算层出不穷，也在很多领域得到了广泛的应用。

考虑到图神经网络对结构信息的捕获能力，在涉及到群体结构的聚类任务上，本文所介绍的聚类算法应该会取得更大的提升。

点击以下标题查看更多往期内容： 

• 图自编码器的起源和应用
  

• ICLR 2020 | 多关系图神经网络CompGCN
  

• 图神经网络三剑客：GCN、GAT与GraphSAGE
  

• 如何快速理解马尔科夫链蒙特卡洛法？
  

• 深度学习预训练模型可解释性概览
  

• ICLR 2020 | 隐空间的图神经网络

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

???? 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

???? 投稿邮箱：

• 投稿邮箱：[email protected] 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

????

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。