08 数据结构与算法之并查集（C语言实现）

8 森林与并查集

并查集是用来解决联通问题的结构
森林是并查集的别名，他俩指代的是同一种结构

8.1 Introduce

8.1.1 Quick-Find算法

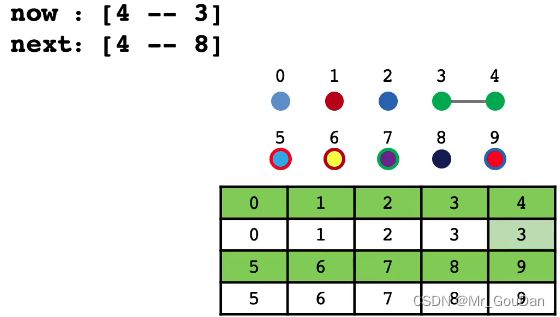
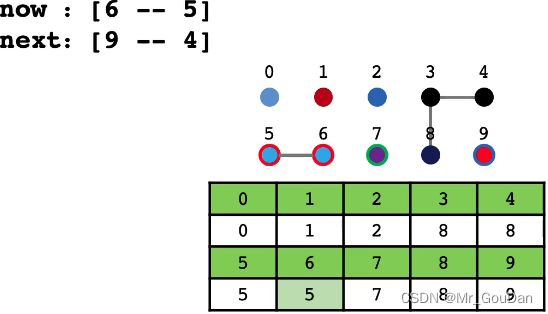
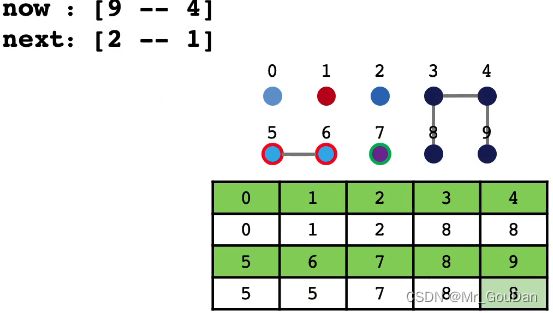
1、基于染色的思想，一开始所有点的颜色不同
2、连接两个点的操作，可以看成将一种颜色的点染成另一种颜色
3、如果两个点颜色一样，证明联通，否则不联通
4、这种方法叫做并查集的:Quick-Find算法】

合并操作流程：

• 合并操作要遍历所有元素时间复杂度O(n)

1、4与3连通：用3号点颜色标记4号点颜色(也可用4号标记3号，规则自定)

2、将4号点的颜色改为3号点标记，

3、4与8连通：只要和4号点颜色相同的点都要改为8号点的颜色

4、6与5连通

5、9与4连通

6、2与1连通

7、5与0连通

8、7与2连通

9、6与1连通

10、合并结束

8.1.2 Quick-find算法总结

1、联通判断:o(1)
2、合并操作:o( n)

问题思考:
1、quick-find算法的联通判断非常快，可是合并操作非常慢
2、本质上问题中只是需要知道一个点与哪些点的颜色相同
3、而若干点的颜色可以通过间接指向同一个节点
4、合并操作时，实际上是将一棵树作为另一棵树的子树

8.1.3 Quick-Union算法

找代表元素，只需修改两个集合中的代表元素,即元素的代表元素。若本身元素的代表元素为本身时，只修改本身元素的代表元素的编号。若不同，则继续再查找本身元素的代表元素，重复上述操作，直到本身元素与本身代表元素相同时，才修改所查找到的元素的代表元素。

8.1.4 Quick-Union算法总结

1、联通判断: tree-height树高
2、合并操作: tree-height树高

问题思考:
1、极端情况下会退化成一条链
2、将节点数量多的接到少的树上面，导致了退化
3、将树高深的接到浅的上面，导致了退化

若要改进，是按照节点数量还是按照树的高度为合并参考? -->>节点数少的树作为子树

8.1.5 练习1

1、quick-find算法最终数组的结果

0	1	2	3	4	5	6	7	8	9
5	5	5	5	5	5	6	6	6	6

2、quick-union算法最终数组的结果

0	1	2	3	4	5	6	7	8	9
1	2	4	4	5	5	6	6	9	7

8.1.6 weighted quick-union算法

weighted quick-union算法是为了避免出现quick-union退化成链表的情况(按秩[节点的权值]优化)

本身元素的代表元素数量和下一个代表元素比较，数量相同，二者均可相互代表。若不等，选择代表元素多的作为代表，替换需要被代表的元素的代表元素，如有多个则选取根节点改为节点数多的那一个

quick-union算法

0	1	2	3	4	5	6	7	8	9
5	1	3	3	1	5	6	6	9	7

weighted quick-union算法

0	1	2	3	4	5	6	7	8	9
1	3	3	3	3	3	9	9	9	9

8.1.7 练习2

quick-union算法

0	1	2	3	4	5	6	7	8	9
1	2	4	4	5	5	6	6	9	7

weighted quick-union算法

0	1	2	3	4	5	6	7	8	9
1	2	4	4	5	5	6	6	9	7

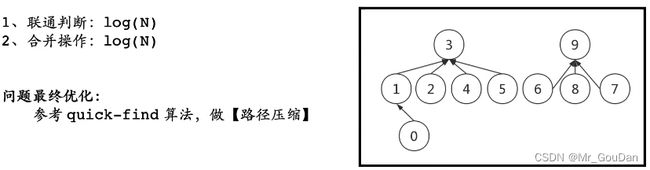
8.1.8 weighted quick-union算法总结

路径压缩：将0号节点挂在3号节点下

8.1.9 并查集相关算法时间复杂度

Algorithm	Constructor	Union	Find
Quick-Find	N	N	1
Quick-Union	N	Tree height	Tree height
Weigthted Quick-Union	N	log N	log N
Weighted Quick-Union With Path Compression	N	Very near to 1(amortized)	Very near to 1(amortized)

扩展阅读：
1、http://blog.csdn.net/dm_vincent/article/details/7655764
2、http://blog.csdn.net/dm_vincent/article/details/7769159

8.2 并查集代码

结合一道算法题展示代码：朋友圈
题目描述：
​ 所谓一个朋友圈子，不一定其中的人都互相直接认识。

​ 例如：小张的朋友是小李，小李的朋友是小王，那么他们三个人属于一个朋友圈。

​ 现在给出一些人的朋友关系，人按照从 1 到 n 编号在这中间会进行询问某两个人是否属于一个朋友圈，请你编写程序，实现这个过程。

输入
第一行输入两个整数 n,m(1≤n≤10000，3≤m≤100000)，分别代表人数和操作数。

接下来 m 行，每行三个整 a,b,c（a∈[1,2], 1≤b,c≤n）
当 a=1 时，代表新增一条已知信息，b,c 是朋友
当 a=2 时，代表根据以上信息，询问 b,c 是否是朋友
输出
对于每个 a=2 的操作，输出『Yes』或『No』代表询问的两个人是否是朋友关系。

样例输入
6 5
1 1 2
2 1 3
1 2 4
1 4 3
2 1 3
样例输出
No
Yes

8.2.1 Quick_find 724ms

#include 
#include 

typedef struct UnionSet {
    int *color;
    int n;//并查集大小
} UnionSet;//结构体别名

UnionSet *init(int n) {
    UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
    u->color = (int *)malloc(sizeof(int) * (n + 1));
    u->n = n;
    for (int i = 1; i <= u->n; i++) {
        u->color[i] = i;
    }
    return u;
} 

int find (UnionSet *u, int x) {
    return u->color[x];//返回对应节点的颜色
}
int merge(UnionSet *u, int a, int b) {//连通a, b
    if (find(u, a) == find(u, b)) return 0;//a,b已经连通
    int color_a = u->color[a];
    for (int i = 1; i <= u->n; i++) {
    		//if (u->color[i] == color_a) {
    		//		 u->color[i] = u->color[b];
    		//}//可根据对偶逻辑改为if (u->color[i] != color_a) continue;
        if (u->color[i] - color_a) continue;
        u->color[i] = u->color[b];
    }
    return 1;
}
void clear(UnionSet *u) {
    if (u == NULL) return ;
    free(u->color);
    free(u);
    return ;
}
int main () {
    int n, m;
    scanf("%d%d", &n, &m);
    UnionSet *u = init(n);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        switch(a) {
            case 1: merge(u, b, c); break;
            case 2: printf("%s\n", find(u, b) == find(u,c) ? "Yes" : "No");
                    break;
        }
    }
    clear(u);
    return 0;
}

8.2.2 Quick_union 1892ms

1．基于找代表元素思想完成的
2.问题思考:
1.极端情况下会退化成—条链
2.将节点数量多的接到少的树下面，导致了退化
3.将树高深的接到浅的下面，导致了退化

#include 
#include 

typedef struct UnionSet {
    int *father;//找代表元素
    int n;
} UnionSet;

UnionSet *init(int n) {
    UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
    u->father = (int *)malloc(sizeof(int) * (n + 1));
    u->n = n;
    for (int i = 1; i <= u->n; i++) {
        u->father[i] = i;
    }
    return u;
} 

int find (UnionSet *u, int x) {
    if (u->father[x] == x) return x;//元素的代表元素是其本身则直接返回，否则，
    return find(u, u->father[x]);//则继续递归查找本身元素的代表元素的代表元素
}
int merge(UnionSet *u, int a, int b) {
    int fa = find(u, a), fb = find(u, b);//a,b的代表元素
    if (fa == fb) return 0;//代表元素相同则不需要合并操作
    u->father[fa] = fb;//可将a的代表元素改为b的代表元素fb
    return 1;
}
void clear(UnionSet *u) {
    if (u == NULL) return ;
    free(u->father);
    free(u);
    return ;
}
int main () {
    int n, m;
    scanf("%d%d", &n, &m);
    UnionSet *u = init(n);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        switch(a) {
            case 1: merge(u, b, c); break;
            case 2: printf("%s\n", find(u, b) == find(u,c) ? "Yes" : "No");
                    break;
        }
    }
    clear(u);
    return 0;
}

8.2.3 Weigth quick_union按秩优化 164ms

相关优化方式
1、weighted quick-union算法
2、按秩(可理解为节点的权重)优化
3、路径压缩

#include 
#include 

#define swap(a, b) {\
    a ^= b; b ^= a; a ^=b;\
}

typedef struct UnionSet {
    int *father, *size;//size为代表元素的这个数的总的节点数
    int n;
} UnionSet;

UnionSet *init(int n) {
    UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
    u->father = (int *)malloc(sizeof(int) * (n + 1));
    u->size= (int *)malloc(sizeof(int) * (n + 1));
    u->n = n;
    for (int i = 1; i <= u->n; i++) {
        u->father[i] = i;
        u->size[i] = 1;//每个节点个数初始化为1
    }
    return u;
} 

int find (UnionSet *u, int x) {
    if (u->father[x] == x) return x;
    return find(u, u->father[x]);
  	//return u->father[x] = find(u, u->father[x]); //路径压缩优化,例如将x->a, a->b, b->c压缩为x->c,a->c,b->c。
}
int merge(UnionSet *u, int a, int b) {
    int fa = find(u, a), fb = find(u, b);
    if (fa == fb) return 0;//代表元素相同则不需要合并
    if (u->size[fa] < u->size[fb]) swap(fa, fb);//fa节点的代表元素(构成树的节点)个数少于fb节点的代表元素个数。假定fa一直记录节点个数多的那个值，fb始终记录节点个数少的值
    u->father[fb] = fa;//fb(节点个数少的子树)作为合并后的子树
    u->size[fa] += u->size[fb];//更新fa元素的节点所在数的节点个数
    return 1;
}
void clear(UnionSet *u) {
    if (u == NULL) return ;
    free(u->father);
    free(u->size);
    free(u);
    return ;
}
int main () {
    int n, m;
    scanf("%d%d", &n, &m);
    UnionSet *u = init(n);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        switch(a) {
            case 1: merge(u, b, c); break;
            case 2: printf("%s\n", find(u, b) == find(u,c) ? "Yes" : "No");
                    break;
        }
    }
    clear(u);
    return 0;
}

8.2.4 quick_union 只加路径压缩 172ms

/*************************************************************************
	> File Name: 19.weigth_union.c_
	> Author: 
	> Mail: 
	> Created Time: Fri 11 Jun 2021 08:38:48 PM CST
 ************************************************************************/
#include 
#include 

typedef struct UnionSet {
    int *father;
    int n;
} UnionSet;

UnionSet *init(int n) {
    UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
    u->father = (int *)malloc(sizeof(int) * (n + 1));
    u->n = n;
    for (int i = 1; i <= u->n; i++) {
        u->father[i] = i;
    }
    return u;
} 

int find (UnionSet *u, int x) {
    if (u->father[x] == x) return x;
		 return u->father[x] = find(u, u->father[x]); //路径压缩优化
}
int merge(UnionSet *u, int a, int b) {
    int fa = find(u, a), fb = find(u, b);
    if (fa == fb) return 0;//代表元素相同则不需要合并
    u->father[fb] = fa;//fb(节点个数少的子树)作为合并后的子树
    return 1;
}
void clear(UnionSet *u) {
    if (u == NULL) return ;
    free(u->father);
    free(u);
    return ;
}
int main () {
    int n, m;
    scanf("%d%d", &n, &m);
    UnionSet *u = init(n);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        switch(a) {
            case 1: merge(u, b, c); break;
            case 2: printf("%s\n", find(u, b) == find(u,c) ? "Yes" : "No");
                    break;
        }
    }
    clear(u);
    return 0;
}

参考链接：https://www.bilibili.com/video/BV19S4y157N3?p=19