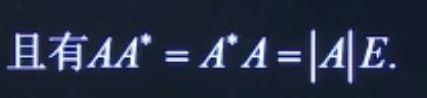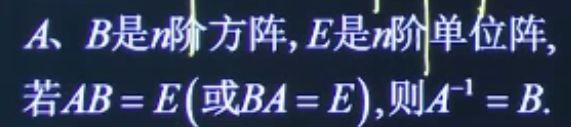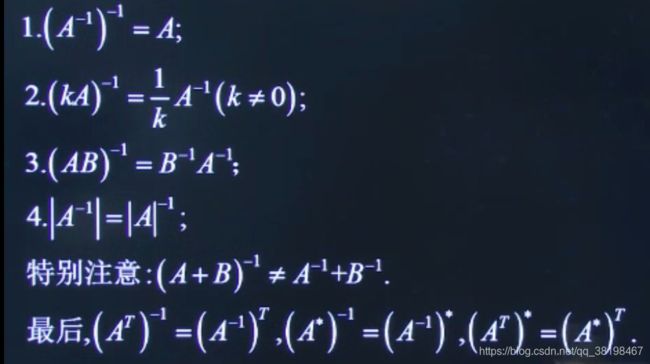线性代数:矩阵及其运算
总体结构图:
矩阵的定义:
由m*n个数,组成的m行n列的表格(注意,这里的表格,表明了矩阵和行列式的本质区别,行列式本质桑是一个数,并且行列式一定是方方正正的,行数和列数一定相等)
而在矩阵中,行和列的数目是不一定相等的,如果行数等于列数,那么这个矩阵就叫做方阵。
再有,如果两个矩阵,他们的行数相等,列数相等,那么这两个矩阵叫做同型矩阵。
最后,如果两个矩阵是同型矩阵,且每一个元素都对应相等,那么才能说这两个矩阵是完全相等的。
几个特殊的矩阵:
1.零矩阵:矩阵的每一个元素都是0,则这个矩阵就是零矩阵,记为0
2.行矩阵和列矩阵:只有一行的矩阵就叫做行矩阵,只有一列的矩阵就叫做列矩阵,同时行矩阵和列矩阵也可以叫做行向量和列向量。
3.单位矩阵:主对角的元素全是1,其他的元素全是0的n阶方阵,注意一定是方阵,不然他喵的就没有主对角呀,通常记为E
4.数量矩阵:主对角的元素全是k,其他的元素全是0的n阶方阵,注意一定是方阵,不然他喵的就没有主对角呀
5.对角矩阵:主对角以外的元素全是0
6.上下三角矩阵:主对角线以下(以上)的元素全为0
注意单位阵、数量阵、对角阵的区别,单位阵主对角只能是1,数量阵主对角只能是一个确定的相同的数,对角阵主对角的元素可以不一样的。
矩阵的运算:
加法运算(必须是同型的矩阵才能相加,也就是行数和列数相同):相加的时候把对应的位置的元素分别相加即可
数乘运算:一个数乘以一个矩阵,用这个数乘以这个矩阵的每一个元素
乘法运算:前提条件是,前面这个矩阵的列数要等于后面矩阵的行数才能进行乘法运算,乘的时候是对应位置的元素相乘再相加,这个怎么理解?也就是说,第一个矩阵的第一行的元素分别乘以第二个矩阵第一列的元素,将他们的结果相加作为结果矩阵的第一行第一列的这个元素,以此类推。这个和上面的数乘运算是有本质区别的。那么乘出来的结果还是一个矩阵,而这个矩阵的行数有前面一个矩阵的行数决定,矩阵的列数由右面一个矩阵的列数决定。且还要注意,两个矩阵相乘,他们的前后位置是有区别的,前后位置不一样,计算出来的结果也可能不一样的。最后再计算矩阵的乘法的时候一定要先判断一下,这两个矩阵到底能否相乘!一定是前面矩阵的列数要等于后面矩阵的行数才能相乘。
通过上面的解释发现,其实矩阵的乘法是没有交换律的,因为啥呢?矩阵的相乘,首先要判断位置,有的时候,AB可以相乘,但是反过来BA就不可以相乘了,反正一条,谨记乘法计算前先判断即可。
而且,如果两个矩阵相乘为0矩阵,是不能说明这两个矩阵一定有一个是零矩阵的!毕竟牵扯的运算规则是不一样的。这个要和我们平时的乘法法则严格区分开来。
总结下来就是下面这个图:
另外记住几个小技巧:
列向量*行向量,且列向量的行数和行向量的列数相等,则乘出来是个方阵。列在前行在后=方阵
行向量*列向量,且行向量的列数等于列向量的行数,则乘出来的是个数,而这个数,就是上面方阵的主对角线的元素之和,而主对角线之和,我们叫做方阵的迹。行在前列在后=数=方阵的迹
两个对角矩阵相乘,结果还是对角矩阵,而且结果矩阵的元素,就是两个对角矩阵的元素分别对应相乘,且再对角矩阵相乘是可以交换的,就是AB=BA
单位矩阵乘以任何矩阵都等于任何矩阵,在乘法中和1的作用差不多
方阵的幂:
一定要是方阵,才能由方阵的幂的这个说法,时刻谨记矩阵相乘的前提条件。
矩阵的转置:
转置很好理解,就是将矩阵的行和列相互换一下,第一行变成第一列,第二行变成第二列,以此类推。比如A矩阵的转置记为![]() ,这里就有特殊情况啦,如果一个矩阵转置之后和原来的矩阵相等,那么这个矩阵就叫做对称矩阵,如果转置之后相差了一个“-”号,那么这个矩阵就是反对称矩阵
,这里就有特殊情况啦,如果一个矩阵转置之后和原来的矩阵相等,那么这个矩阵就叫做对称矩阵,如果转置之后相差了一个“-”号,那么这个矩阵就是反对称矩阵
矩阵转置的运算性质:
正交矩阵:
如果一个矩阵乘以自己的转置结果为单位矩阵,那么这个矩阵就是正交矩阵
方阵的行列式:
因为行列式一定是四四方方的,所以在矩阵中只有方阵满足这个条件,而在方阵中,由方阵的元素构成的行列式,称为这个方正的行列式。比如方阵A,那么他的行列式就记为 |A|
方正行列式的性质:
伴随矩阵:
定义:用|A|(也就是A这个矩阵的行列式)的代数余子式,按照一定的形式拼成的矩阵称为矩阵A的伴随矩阵,记为![]()
上面说到了按照一定形式,那么到底是个什么形式?就是下面这个图的形式
按照上面的这个图我们可以看出来,实际上就是取的A矩阵的每一个元素的代数余子式,记住,![]() 表示的是一个行列是的代数余子式。ok,但是我们发现他们的位置似乎有些不一样,那里不一样呢?我们稍微观察一下就可以知道,如果全是按照相应的位置放置的代数余子式的话,那第一排的元素应该为
表示的是一个行列是的代数余子式。ok,但是我们发现他们的位置似乎有些不一样,那里不一样呢?我们稍微观察一下就可以知道,如果全是按照相应的位置放置的代数余子式的话,那第一排的元素应该为![]() ,
,![]() ....一直到
....一直到![]() 。但是发现没有,巧了的就是,这样的排列,却刚刚好排到了第一列,再看第二列,是不是本来应该恰巧是原来第二行的?第n列也是如此,所以,我们发现了规律,也就是说,将一个矩阵的行列式的每一个元素,先求出它们的代数余子式,先保持他们的位置不要动,然后将原来第一行的放到第一列,第二行的放到第二列,第三行的放到第三列,第n行的放到第n列。。。这样形成的矩阵,我们就叫做伴随矩阵。
。但是发现没有,巧了的就是,这样的排列,却刚刚好排到了第一列,再看第二列,是不是本来应该恰巧是原来第二行的?第n列也是如此,所以,我们发现了规律,也就是说,将一个矩阵的行列式的每一个元素,先求出它们的代数余子式,先保持他们的位置不要动,然后将原来第一行的放到第一列,第二行的放到第二列,第三行的放到第三列,第n行的放到第n列。。。这样形成的矩阵,我们就叫做伴随矩阵。
伴随矩阵的重要公式:
也即是,一个矩阵乘以他的伴随矩阵,其值等于这个矩阵的行列式乘以单位阵
伴随矩阵的性质:
实际上呢伴随矩阵的性质都来源于上面说的那个重要公式,其实通过上面的你可以发现,这组公式应该和转置的公式对比起来看,因为他们很多都是相似的,只是结果是不一样的。
伴随矩阵的求法:
很明显,定义法是只能用在低阶的矩阵,因为想想看,如果是高阶,每一个都要求它的代数余子式,计算量陡然增加,效率极低。很明显不适合我们用来解题,所对于我们遇到的大部分题目,我们都使用公式法进行解决。这里要注意一下,这个公式的后面不是A的负一次方,这个表示的是矩阵A的逆矩阵。
需要记住的几个一般规律:
如果一个矩阵是二阶矩阵,那么他的伴随矩阵的元素就是这个原来矩阵的主对角线上的元素位置互换一下,然后副对角线的元素正负号改变一下即可,简单来讲记住一句话:关于二阶矩阵的伴随矩阵,主对调,副变号
逆矩阵:
定义:
我们来看一下,首先逆矩阵说的是两个矩阵,是谁是谁的逆矩阵,而不是一个矩阵,然后要求,这两个矩阵都是方阵,且阶次相同,这个一定要注意!,最后注意一点,一定是要满足AB=BA=E才是满足定义的,如果只是有一个等号成立是不行的。这就是不满足定义。
另外一点,如果这个条件成立的话,他们两个是相互称为对方的逆矩阵的,而不是说谁是谁的逆矩阵后另外一个不是谁的逆矩阵,他们是不分主次的。
逆矩阵的定理:
如果一个矩阵可逆,那么他的逆矩阵一定是唯一的,记住,一定是唯一的。不可能还冒出来两个逆矩阵
如果一个矩阵可逆,那么可以推出这个矩阵的行列式一定不等于0,反过来也可以推,就是说如果一个矩阵的行列式不等于0,那么这个矩阵就一定可逆,他们两个是充分必要条件。
逆矩阵的推论:
咋一看,着他喵的和定义有社么区别码?其实仔细看一下,还是有区别的,我们的定义说的是AB=BA=E才能说明这两个矩阵是互为逆矩阵的,但是这里是说了AB=E或者BA=E,只要满足条件的一半就能说明这两个矩阵可逆,从计算量上来讲,我们的计算量就少了一半。所以我们以后证明的时候往往用的是这个推论而不用定义法,毕竟效率也是很重要的。
但是还要注意,A和B还是要满足他们都是方阵,且阶数相等。
逆矩阵的性质:
看看看,又是和伴随以及转置差不多的那几条性质吧,但是这里要注意一下第四条,那里说的是矩阵A的逆矩阵的行列式等于矩阵A的行列式的倒数,注意后面是倒数,为什么是倒数,搞清楚行列式的实质就行,我们说了,行列式就是一个数,而矩阵是一个表格,所以只有数才有倒数呀,矩阵那里来的倒数。
另外最后那里,我们注意到,他其实就是说,转置、伴随、逆这三个谁先求后求都无所谓,相当于是同级运算。
逆矩阵的求法:
这里要清楚,实际上,我们方法二,也就是用伴随来求逆矩阵是不常用的,因为求伴随毕竟要求代数余子式,这样的话就是计算比较复杂,但是如果一定要用伴随来求,那也没办法,我们就i首先不考虑他,另外伴随求逆矩阵,一般用在二阶,三阶。因为这样的矩阵计算量才不大。
方法一和方法三才是重点:
方法三,什么是初等变换,就是说你通过等价代换的手段得到你想要的你表矩阵,方法三的意思是什么呢,就是说,你把一个矩阵和单位阵放在一起,经过初等变换,当你把原来的矩阵变成单位阵之后,那么原来单位阵的地方其实就已经变成了你这个矩阵的逆矩阵了。
那么什么时候用这些方法呢?记住两点
如果矩阵的元素没有告诉你,也就是说他是一个抽象的矩阵,那你就用定义法,如果矩阵的元素都告诉你了,那你就用初等变换。
需要记住的矩阵运算小技巧:
当我们遇见这种矩阵的时候,它的幂是有规律的,什么规律呢?现在这个是矩阵B,那么B的2次方应该是其他的元素不变,右上角的c元素变成旁边两个元素的乘积,也就是ab,而原来a和b的位置应该变成0,而从B的3此方开始以及以后的n次方,这个矩阵的值都是0。这就是这样的矩阵他的幂运算的规律。
分块矩阵:
因为矩阵不是一个二维的表格嘛,既然这样的话,那我们其实就可以在原来的基础上,让一些元素在抱成一团,这样我们就可以把他们在分一下。
比如现在有A这个矩阵,我中间横着切一刀,然后再竖着切一刀,就把他分成了四大块,那么这四大块分别又是一个矩阵,这样的矩阵我们就叫分块矩阵,分块矩阵一般是在元素比较多的时候我们可以这样做来简化操作使用。
但是我们注意一下,分块的方式其实是多种多样的,所以下面有两个我们以后常用的分块方式。
第一种:按行分块,就拿上面的这个A矩阵来说,我把第一行分成一块,第二行分成一块,同样的第三块分成一块,这样分下来就是按行分块的分块矩阵。
第二种:按列分块,和上面的对比起来,就是把每一列当成一块来分。
ok,把矩阵按照上面的两种方式来分的话是不是就分成了我们熟悉的行向量和列向量了?其实就是行矩阵和列矩阵。
分块矩阵的运算:
分块矩阵说到底还是矩阵,所以它有这矩阵的运算性质,
分块矩阵的性质:
第一个其实就是类比的对角矩阵的性质来的。
初等变换和初等矩阵:
矩阵的初等变换有以下三种形式,对于行的变换我们叫初等行变换,列的变换呢,我们叫初等列变换
但是千万要注意,我们千万不能和行列式的等价代换搞混淆,行列式也有类似的性质,但是他是叫等价代换,换来换去都是原来的那个行列式,但是矩阵的初等变换则不一样。它是通过一个矩阵变换为另外一个矩阵。他们之间可能是不等的。
初等矩阵:
什么是初等矩阵?就是单位矩阵经过一次的初等变换而得到的矩阵,这种矩阵就是我们说的初等矩阵。经过上面说的初等变换不止一种变换,所以初等矩阵的表现形式也不止一种,这里一定要注意到。
初等矩阵的性质:
性质一:
初等矩阵都是可逆矩阵,而且它的逆矩阵仍然是同一类型的初等矩阵。
什么意思呢?也就是说,初等矩阵的逆,都有自己的特定结论,比如下面这个图。
什么意思呢?我们知道,初等矩阵实际上是单位阵经过了一次三种初等变换中的一种而的来的,那么对于这三种类型的初等变换它的逆矩阵其实是有特定的结果的。
比如上面这个,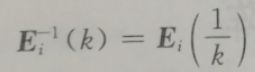 ,它表示的是,如果一个初等矩阵是单位阵的某一行或者某一列乘以了某一个数而得来的。那么这个初等矩阵的逆矩阵实际上也是单位阵对应那一行或者那一列乘以对应数的倒数。就好比上图中的
,它表示的是,如果一个初等矩阵是单位阵的某一行或者某一列乘以了某一个数而得来的。那么这个初等矩阵的逆矩阵实际上也是单位阵对应那一行或者那一列乘以对应数的倒数。就好比上图中的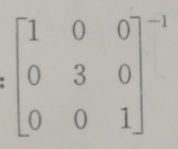
它表示的是单位阵第二行或者第二列乘以3而得来的初等矩阵。那么它的逆矩阵实际上就是单位阵第二行或者第二列乘以1/3而得来。
这里就明白了这个性质一的原理,其他两种情况和第一种是一样的理解。比如第二种,他表示的是经过单位阵两行(列)交换得来的,那么它的逆矩阵就是和原来的初等矩阵是一样的。第三种呢,它表示单位阵的某一行(列)乘以一个数再加到另外一行(列)上,而它的逆矩阵呢实际上和他的操作是一样的,不过要加一个负号。
注意一下,可能还是没有理解什么是同一类型的初等矩阵,它其实就是指的变换方式一样,比如一个初等矩阵,它是单位阵经过某一行(列)倍乘过来的,那么它的逆矩阵肯定也是经过单位阵的某一行(列)倍乘得来的。
性质二:
左乘和右乘
什么意思呢?就是说,如果一个矩阵A它的左边或者右边乘以一个初等矩阵,那么它的效果就相当于对这个矩阵A做了相同类型的初等行或者列变换。注意,左乘表示行变换,右乘表示列变换,这是有很大区别的,一定要注意区分。
比如说,矩阵A左边乘了一个初等矩阵B,这个B呢是由单位阵第二行乘以2变过来的,那么这样一乘,就表示BA就等于A矩阵的第二行乘以2,这就是上面这句话的意思。
用初等变换求逆矩阵:
什么意思呢?将矩阵A和单位阵放在一起,当这A矩阵这个位置变换成为单位矩阵的时候,原来单位阵的位置就已经变成了A的逆矩阵的样子了。同样的竖着放也是一样的。
这就是竖着放的情况,当A这里变成单位阵的时候E这里就变成了A的逆了。
矩阵的等价:
定义:
一个矩阵经过有限次的初等变换变到B,称A和B等价,记为A![]() B
B
两个矩阵等价的充要条件:
后面r(A)=r(B)说的是矩阵的秩相等,那么也能证明这两个矩阵的等价的。
矩阵的秩:
定义:
矩阵A中非零子式的最高阶数称为矩阵A的秩,记为r(A);
那么什么叫子式呢?其实是这样的,比如我们现在有一个n*m的矩阵,那么再这个矩阵中任取k行,任取k列,那么这个取出来的k行和k阶拼成的一个k阶行列式就是这个矩阵的k阶子式。这个就是子式的概念,说白了,子式就是行列式。上面说的非零子式,其实就是非零的行列式嘛。注意这里是任意取的行数和列数,说明一定是要取出来的行数和列数构成的行列式都要满足这个条件才行。
上面还说了最高阶数,那其实就是如果这个矩阵存在子式,那个这个子式,的最高阶数,比如5阶,那么这个5就是这个矩阵的秩。
举个栗子:下面这个2*3阶行列式
那么它的秩是多少?很明显,子式一定是方阵的阶数。记住,行列式不等于零,行列式实际上就是一个数嘛,我们都知道,所以一定是这个行列式计算出来不等于0才管用的。但是我们发现,这里随便怎么取出两行两列,它的行列式都等于0,所以这个不满足它非零子式的要求,所以这里矩阵的秩就只能为1,不能是2,虽然它看上去特别像2。
但是我们发现,这个亚子去确定矩阵的秩其实是比较麻烦的。我们一般用下面的或者方法。
定理:
矩阵的秩其实就等于它对应的行阶梯形矩阵非零行的行数。就是说这个梯形矩阵,它有几行不为零,它的秩就是多少。
那么什么又是行阶梯形矩阵呢?行阶梯形矩阵说的就是,这个矩阵的零行(就是一行的元素全是零)在最下面,并且每一行从左边起的第一个元素,它下面的元素必须全部是零,这种矩阵就是我们说的行阶梯形矩阵。
这里就有一个小的注意点了。初等变换是不会改变矩阵的秩的。所以我们以后求一个具体的矩阵的秩,往往可以通过初等变换来求。
秩的性质:
上面我们知道求一个具体矩阵的秩,可以用初等变换的形式来求,但是很多时候我们会碰到抽象矩阵,这个时候就要用到秩的性质了。
注意第七个,用的比价多。