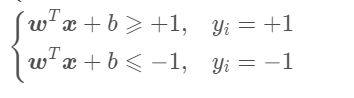#《机器学习》_周志华(西瓜书)&南瓜书_第6章 支持向量机
待做:
- P134-P139理论部分
- 整理习题,补充
问题:
1、距离计算
2、线性核和高斯核?
第6章 支持向量机
6.1 间隔与支持向量
基于训练集 D D D在样本空间中找到一个划分超平面。
- 对训练样本局部扰动的容忍性最好。
1、划分超平面: w T x + b = 0 \boldsymbol{w}^T\boldsymbol{x}+b=0 wTx+b=0
其中 w = { w 1 ; w 2 ; . . . ; w d } \boldsymbol{w}=\left\{w_1;w_2;...;w_d\right\} w={w1;w2;...;wd}为法向量,决定了超平面的方向。
b b b为位移项,决定了超平面与原点之间的距离。
2、样本空间中任意点 x \boldsymbol{x} x到超平面 ( w , b ) 的 距 离 可 写 为 : (\boldsymbol{w},b)的距离可写为: (w,b)的距离可写为:
r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ r=\frac{|\boldsymbol{w}^T\boldsymbol{x}+b|}{||\boldsymbol{w}||} r=∣∣w∣∣∣wTx+b∣
分类预测:
{ w T x i + b > 0 , y i = + 1 w T x i + b < 0 , y i = − 1 \left\{ \begin{aligned} \boldsymbol{w}^T\boldsymbol{x}_i+b > 0,& & y_i=+1\\ \boldsymbol{w}^T\boldsymbol{x}_i+b < 0,& & y_i=-1 \\ \end{aligned} \right. {wTxi+b>0,wTxi+b<0,yi=+1yi=−1
令
{ w T x + b ⩾ + 1 , y i = + 1 w T x + b ⩽ − 1 , y i = − 1 \left\{ \begin{aligned} \boldsymbol{w}^T\boldsymbol{x}+b \geqslant +1,& & y_i=+1\\ \boldsymbol{w}^T\boldsymbol{x}+b \leqslant -1,& & y_i=-1 \\ \end{aligned} \right. {wTx+b⩾+1,wTx+b⩽−1,yi=+1yi=−1
?
这个1是怎么选定的呢?
支持向量: 使上式等号成立的训练样本点
间隔: 两个异类支持向量到超平面的距离。
γ = 2 ∣ ∣ w ∣ ∣ γ=\frac{2}{||\boldsymbol{w}||} γ=∣∣w∣∣2
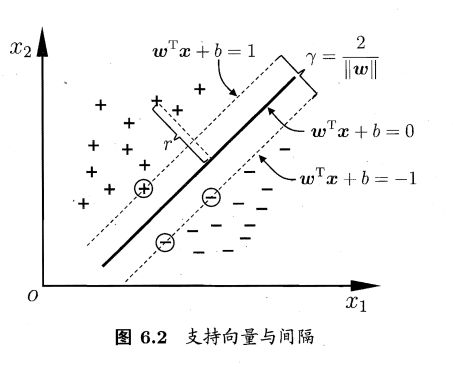
最大化间隔,等价于最小化 ∣ ∣ w ∣ ∣ 2 ||\boldsymbol{w}||^2 ∣∣w∣∣2
支持向量机(Support Vector Machine)的基本型:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 \min\limits_{\boldsymbol{w},b}\frac{1}{2}||\boldsymbol{w}||^2 w,bmin21∣∣w∣∣2
s.t. y i ( w T x i + b ) ⩾ 1 , i = 1 , 2 , , . . . m . y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\geqslant 1, i=1,2,,...m. yi(wTxi+b)⩾1,i=1,2,,...m.
6.2 对偶问题
拉格朗日乘子法:
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) L(\boldsymbol{w},b,\boldsymbol{α})=\frac{1}{2}||\boldsymbol{w}||^2+\sum\limits_{i=1}^mα_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) L(w,b,α)=21∣∣w∣∣2+i=1∑mαi(1−yi(wTxi+b))
拉格朗日乘子: α = ( α 1 ; α 2 ; . . . ; α m ) α=(α_1;α_2;...;α_m) α=(α1;α2;...;αm)
令 L ( w , b , α ) L(\boldsymbol{w},b,\boldsymbol{α}) L(w,b,α)对 w 和 b \boldsymbol{w}和b w和b的偏导为0,得
w = ∑ i = 1 m α i y i x i , 0 = ∑ i = 1 m α i y i \boldsymbol{w}=\sum\limits_{i=1}^mα_iy_i\boldsymbol{x}_i,\\ 0=\sum\limits_{i=1}^mα_iy_i w=i=1∑mαiyixi,0=i=1∑mαiyi
支持向量机基本型的对偶问题:
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j \max\limits_{α}\sum\limits_{i=1}^mα_i-\frac{1}{2}\sum\limits_{i=1}^m\sum\limits_{j=1}^mα_iα_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj
s.t. ∑ i = 1 m α i y i = 0 , α i ⩾ 0 , i = 1 , 2 , . . . , m \sum\limits_{i=1}^mα_iy_i=0,\\ α_i\geqslant0,i=1,2,...,m i=1∑mαiyi=0,αi⩾0,i=1,2,...,m
模型:
f ( x ) = w T x + b = ∑ i = 1 m α i y i x i T x + b f(\boldsymbol{x}) =\boldsymbol{w}^T\boldsymbol{x}+b\\ = \sum\limits_{i=1}^mα_iy_i\boldsymbol{x}_i^T\boldsymbol{x}+b f(x)=wTx+b=i=1∑mαiyixiTx+b
KKT条件(Karush-Kuhn-Tucker):
{ α i ⩾ 0 ; y i f ( x i ) − 1 ⩾ 0 ; α i ( y i f ( x i ) − 1 ) = 0. \left\{ \begin{aligned} &α_i\geqslant0;\\ &y_if(\boldsymbol{x}_i)-1\geqslant0; \\ &α_i(y_if(\boldsymbol{x}_i)-1)=0. \end{aligned} \right. ⎩⎪⎨⎪⎧αi⩾0;yif(xi)−1⩾0;αi(yif(xi)−1)=0.
对任意训练样本 ( x i , y i ) (\boldsymbol{x}_i,y_i) (xi,yi),总有 α i α_i αi=0或 y i f ( x i ) = 1 y_if(\boldsymbol{x}_i)=1 yif(xi)=1
- 若 α i α_i αi=0,则该样本不会在模型中出现,即不会对 f ( x ) f(\boldsymbol{x}) f(x)有任何影响。
- 若 α i α_i αi>0,则必有 y i f ( x i ) = 1 y_if(\boldsymbol{x}_i)=1 yif(xi)=1,所对应的样本位于最大间隔边界上,是一个支持向量。
可见,训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关。
求解对偶问题:
SMO(Sequential Minimal Optimization):
1、选取一对需要更新的变量 α i α_i αi和 α j α_j αj;
2、固定 α i α_i αi和 α j α_j αj以外的参数,求解式(6.11)获得更新后的 α i α_i αi和 α j α_j αj。
3、不断循坏步骤1和2,直至收敛。
@SMO算法&&对偶问题的相关推导 P125
6.3 核函数
针对非线性可分问题:
- 将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。
用 ϕ ( x ) \phi(\boldsymbol{x}) ϕ(x)替换 x \boldsymbol{x} x
令 ϕ ( x ) 表 示 将 x 映 射 后 的 特 征 向 量 。 \phi(\boldsymbol{x})表示将\boldsymbol{x}映射后的特征向量。 ϕ(x)表示将x映射后的特征向量。
对应的模型:
f ( x ) = w T ϕ ( x ) + b f(\boldsymbol{x}) =\boldsymbol{w}^T\phi(\boldsymbol{x})+b f(x)=wTϕ(x)+b
对应的支持向量机(Support Vector Machine)的基本型:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 \min\limits_{\boldsymbol{w},b}\frac{1}{2}||\boldsymbol{w}||^2 w,bmin21∣∣w∣∣2
s.t. y i ( w T ϕ ( x i ) + b ) ⩾ 1 , i = 1 , 2 , , . . . m . y_i(\boldsymbol{w}^T\phi(\boldsymbol{x}_i)+b)\geqslant 1, i=1,2,,...m. yi(wTϕ(xi)+b)⩾1,i=1,2,,...m.
对应的对偶问题:
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ϕ ( x i ) T ϕ ( x j ) \max\limits_{α}\sum\limits_{i=1}^mα_i-\frac{1}{2}\sum\limits_{i=1}^m\sum\limits_{j=1}^mα_iα_jy_iy_j\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x}_j) αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjϕ(xi)Tϕ(xj)
s.t. ∑ i = 1 m α i y i = 0 , α i ⩾ 0 , i = 1 , 2 , . . . , m \sum\limits_{i=1}^mα_iy_i=0,\\ α_i\geqslant0,i=1,2,...,m i=1∑mαiyi=0,αi⩾0,i=1,2,...,m
@核函数引入 推导 P127
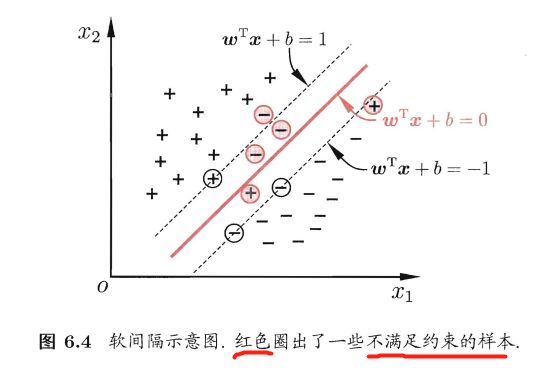
6.4 软间隔与正则化
不好断定这个线性可分的结果是不是过拟合造成的。
软间隔(soft margin): 允许某些样本不满足约束。
硬间隔(hard margin): 所有样本都必须划分正确。
优化目标:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ℓ 0 / 1 ( y i ( w T x i + b ) − 1 ) \min\limits_{\boldsymbol{w},b}\frac{1}{2}||\boldsymbol{w}||^2+C\sum\limits_{i=1}^m\ell_{0/1}(y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)-1) w,bmin21∣∣w∣∣2+Ci=1∑mℓ0/1(yi(wTxi+b)−1)
其中 C > 0 C>0 C>0为常数, ℓ 0 / 1 \ell_{0/1} ℓ0/1是“0/1损失函数”
ℓ 0 / 1 = { 1 , i f z < 0 ; 0 , o t h e r w i s e . \ell_{0/1}=\left\{ \begin{aligned} 1,& &if\quad z<0;\\ 0,& & otherwise. \\ \end{aligned} \right. ℓ0/1={1,0,ifz<0;otherwise.
ℓ 0 / 1 \ell_{0/1} ℓ0/1非凸、非连续,数学性质不太好。
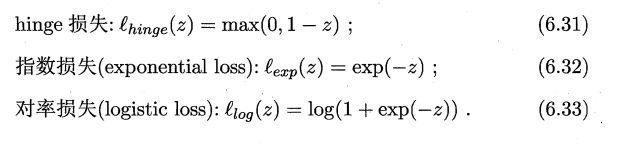

采用hinge损失:
采用hinge损失的优化目标:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m max ( 0 , 1 − y i ( w T x i + b ) ) \min\limits_{\boldsymbol{w},b}\frac{1}{2}||\boldsymbol{w}||^2+C\sum\limits_{i=1}^m\max(0,1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) w,bmin21∣∣w∣∣2+Ci=1∑mmax(0,1−yi(wTxi+b))
引入松弛变量 ξ i ⩾ 0 ξ_i\geqslant 0 ξi⩾0,
软间隔支持向量机:
min w , b , ξ i 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ξ i \min\limits_{\boldsymbol{w},b,ξ_i}\frac{1}{2}||\boldsymbol{w}||^2+C\sum\limits_{i=1}^mξ_i w,b,ξimin21∣∣w∣∣2+Ci=1∑mξi
s.t. y i ( w T x i + b ) ⩾ 1 − ξ i y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\geqslant1-ξ_i yi(wTxi+b)⩾1−ξi
ξ i ⩾ 0 , i = 1 , 2 , . . . , m . ξ_i\geqslant0,i=1,2,...,m. ξi⩾0,i=1,2,...,m.
松弛变量: 表征样本不满足约束的程度。
拉格朗日函数
L ( w , b , α , ξ , μ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ξ i + ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 m μ i ξ i L(\boldsymbol{w},b,\boldsymbol{α},ξ,μ)=\frac{1}{2}||\boldsymbol{w}||^2+C\sum\limits_{i=1}^mξ_i+\sum\limits_{i=1}^mα_i(1-ξ_i-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b))-\sum\limits_{i=1}^mμ_iξ_i L(w,b,α,ξ,μ)=21∣∣w∣∣2+Ci=1∑mξi+i=1∑mαi(1−ξi−yi(wTxi+b))−i=1∑mμiξi
其中拉格朗日乘子: α i ⩾ 0 , μ i ⩾ 0 α_i\geqslant0,μ_i\geqslant0 αi⩾0,μi⩾0
令 L ( w , b , α , ξ , μ ) L(\boldsymbol{w},b,\boldsymbol{α},ξ,μ) L(w,b,α,ξ,μ)对 w , b , ξ i \boldsymbol{w},b,ξ_i w,b,ξi的偏导为0,得
w = ∑ i = 1 m α i y i x i , 0 = ∑ i = 1 m α i y i C = α i + μ i \boldsymbol{w}=\sum\limits_{i=1}^mα_iy_i\boldsymbol{x}_i,\\ 0=\sum\limits_{i=1}^mα_iy_i\\ C=α_i+μ_i w=i=1∑mαiyixi,0=i=1∑mαiyiC=αi+μi
得到的对偶问题:
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j \max\limits_{\boldsymbol{α}}\sum\limits_{i=1}^mα_i-\frac{1}{2}\sum\limits_{i=1}^m\sum\limits_{j=1}^mα_iα_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj
s.t. ∑ i = 1 m α i y i = 0 , 0 ⩽ α i ⩽ C , i = 1 , 2 , . . . , m \sum\limits_{i=1}^mα_iy_i=0,\\ 0\leqslantα_i\leqslant C,i=1,2,...,m i=1∑mαiyi=0,0⩽αi⩽C,i=1,2,...,m (只有这里有区别)
软硬间隔的差别在于对对偶变量的约束不同:
- 软间隔 0 ⩽ α i ⩽ C 0\leqslantα_i\leqslant C 0⩽αi⩽C
- 硬间隔 0 ⩽ α i 0\leqslantα_i 0⩽αi
软间隔支持向量机的KKT条件:
{ α i ⩾ 0 , μ i ⩾ 0 , y i f ( x i ) − 1 + ξ i ⩾ 0 ; α i ( y i f ( x i ) − 1 + ξ i ) = 0 , ξ i ⩾ 0 , μ i ξ i = 0. \left\{ \begin{aligned} &α_i\geqslant0,\quad μ_i\geqslant0,\\ &y_if(\boldsymbol{x}_i)-1+ξ_i\geqslant0; \\ &α_i(y_if(\boldsymbol{x}_i)-1+ξ_i)=0,\\ &ξ_i\geqslant0,\quad μ_iξ_i=0. \end{aligned} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧αi⩾0,μi⩾0,yif(xi)−1+ξi⩾0;αi(yif(xi)−1+ξi)=0,ξi⩾0,μiξi=0.
对任意训练样本 ( x i , y i ) (\boldsymbol{x}_i,y_i) (xi,yi),总有 α i = 0 或 y i f ( x i ) = 1 − ξ i α_i=0或y_if(\boldsymbol{x}_i)=1-ξ_i αi=0或yif(xi)=1−ξi。
1、若 α i = 0 α_i=0 αi=0,则样本不会对 f ( x ) f(\boldsymbol{x}) f(x)有影响。
2、若 α i > 0 α_i>0 αi>0,则必有 y i f ( x i ) = 1 − ξ i y_if(\boldsymbol{x}_i)=1-ξ_i yif(xi)=1−ξi,该样本是支持向量。
3、若 α i < C α_i
4、若 α i = C α_i=C αi=C,则 μ i = 0 μ_i=0 μi=0
- 若 ξ i ⩽ 1 ξ_i\leqslant1 ξi⩽1,样本落在最大间隔内部
- 若 ξ i > 1 ξ_i>1 ξi>1,样本被错误分类
hinge损失函数保持了稀疏性。
支持向量机 VS 对率回归
支持向量机 VS 对率回归
1、性能相当
2、对率回归在给出预测标记的同时也给出了概率;对率回归能直接用于多分类任务。
3、hinge损失有一块平坦的零区域,使得支持向量机的解具有稀疏性,而对率损失是光滑的单调递减函数,无类似概念。
- 对率回归的解依赖于更多的训练样本,其预测开销更大。
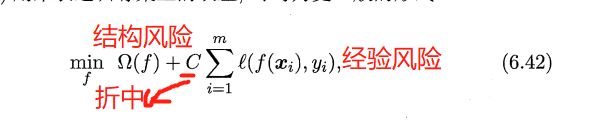
第一项描述划分超平面的间隔大小
第二项表述训练集上的误差,用于描述模型与训练数据的契合程度。
L 2 范 数 L_2范数 L2范数和 L 1 范 数 L_1范数 L1范数
L 2 范 数 L_2范数 L2范数倾向于 w \boldsymbol{w} w的分量取值尽量均衡,即非零向量的个数尽量稠密。
- 含0少,稠密,L2
L 0 范 数 L_0范数 L0范数和 L 1 范 数 L_1范数 L1范数倾向于 w \boldsymbol{w} w的分量取值尽量稀疏,即非零向量的个数尽量少。
- 含0多,稀疏,L1,L0
正则化: 罚函数法
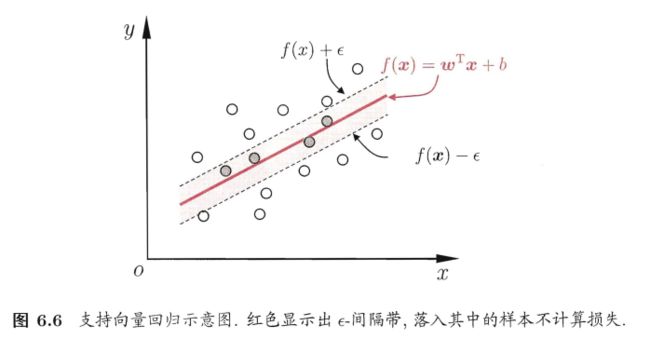
6.5 支持向量回归(SVR)
问题:
给定训练样本 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } , y i ∈ R D=\left\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),...,(\boldsymbol{x}_m,y_m)\right\}, y_i\in \mathbb{R} D={(x1,y1),(x2,y2),...,(xm,ym)},yi∈R,学习一个回归模型,使得 f ( x ) 与 y f(\boldsymbol{x})与y f(x)与y尽可能接近, w 和 b \boldsymbol{w}和b w和b是待确定的参数。
SVR问题的优化目标:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ℓ ϵ ( f ( x i ) − y i ) \min\limits_{\boldsymbol{w},b}\frac{1}{2}||\boldsymbol{w}||^2+C\sum\limits_{i=1}^m\ell_\epsilon(f(\boldsymbol{x}_i)-y_i) w,bmin21∣∣w∣∣2+Ci=1∑mℓϵ(f(xi)−yi)
其中 C C C为正则化常数, ℓ ϵ \ell_\epsilon ℓϵ是 ϵ − \epsilon- ϵ−不敏感损失函数
ℓ ϵ ( z ) = { 0 , i f ∣ z ∣ ⩽ ϵ ; z − ϵ , o t h e r w i s e . \ell_\epsilon(z)=\left\{ \begin{aligned} 0,& &if\quad |z|\leqslant\epsilon;\\ z-\epsilon,& & otherwise. \\ \end{aligned} \right. ℓϵ(z)={0,z−ϵ,if∣z∣⩽ϵ;otherwise.
引入松弛变量 ξ i 和 ξ i ^ ξ_i和\hat{ξ_i} ξi和ξi^,
优化目标变成:
min w , b , ξ i , ξ i ^ 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ( ξ i , ξ i ^ ) \min\limits_{\boldsymbol{w},b,ξ_i,\hat{ξ_i}}\frac{1}{2}||\boldsymbol{w}||^2+C\sum\limits_{i=1}^m(ξ_i,\hat{ξ_i}) w,b,ξi,ξi^min21∣∣w∣∣2+Ci=1∑m(ξi,ξi^)
s.t. f ( x i ) − y i ⩽ ϵ + ξ i f(\boldsymbol{x}_i)-y_i\leqslant\epsilon+ξ_i f(xi)−yi⩽ϵ+ξi
y i − f ( x i ) ⩽ ϵ + ξ i ^ y_i-f(\boldsymbol{x}_i)\leqslant\epsilon+\hat{ξ_i} yi−f(xi)⩽ϵ+ξi^
ξ i ⩾ 0 , ξ i ^ ⩾ 0 , i = 1 , 2 , . . . , m . ξ_i\geqslant0,\hat{ξ_i}\geqslant0,i=1,2,...,m. ξi⩾0,ξi^⩾0,i=1,2,...,m.
@对偶问题
核方法
6.7
线性核SVM, 文本分类, 1998
习题
6.1
6.1 试证明样本空间中任意点 x \boldsymbol{x} x到超平面 ( w , b ) (\boldsymbol{w},b) (w,b)的距离为式 (6.2)。
对于超平面 ( w , b ) (\boldsymbol{w},b) (w,b),有 w T x 0 + b = 0 \boldsymbol{w}^T\boldsymbol{x}_0+b=0 wTx0+b=0 ,则 − w T x 0 = b -\boldsymbol{w}^T\boldsymbol{x}_0=b −wTx0=b
- x 0 \boldsymbol{x}_0 x0是为了和 x \boldsymbol{x} x作区分,表示超平面上的任意点。
样本空间中任意点 x \boldsymbol{x} x到超平面 ( w , b ) (\boldsymbol{w},b) (w,b)的距离为 点 x \boldsymbol{x} x与点 x 0 \boldsymbol{x}_0 x0之间的向量 x − x 0 \boldsymbol{x}-\boldsymbol{x}_0 x−x0在超平面的法向量 w \boldsymbol{w} w上的投影,根据投影计算公式,
r = ∣ w T ( x − x 0 ) ∣ ∣ ∣ w ∣ ∣ = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ r=\frac{|\boldsymbol{w}^T(\boldsymbol{x}-\boldsymbol{x}_0)|}{||\boldsymbol{w}||}=\frac{|\boldsymbol{w}^T\boldsymbol{x}+b|}{||\boldsymbol{w}||} r=∣∣w∣∣∣wT(x−x0)∣=∣∣w∣∣∣wTx+b∣
6.2
6.2 试使用 LIBSVM,在西瓜数据集 3.0α 上分别用线性核和高斯核训练一个 SVM,并比较其支持向量的差别.
参考1
6.3
6.3 选择两个 UCI 数据集,分别用线性核和高斯核训练一个 SVM ,并与BP 神经网络和 C4.5 决策树进行实验比较.
6.4
6.4 试讨论线性判别分析与线性核支持向量机在何种条件 等价.
6.5
6.5 试述高斯核 SVM与RBF 神经网络之间的联系.
6.6
6.6 试析 SVM 对噪声敏感的原因.
6.7
6.7 试给出式(6.52) 的完整 KKT 条件.
6.8
6.8 以西瓜数据集 3.0α 的"密度"为输入"含糖率"为输出,试使用LIBSVM 训练一个 SVR
6.9
6.9 试使用核技巧推广对率回归?产生"核对率回归"
6.10
6.10 试设计一个能显著减少 SVM 中支持向量的数目而不显著降低泛化性能的方法.
LaTeX字符
LaTeX字符链接https://blog.csdn.net/weixin_42612337/article/details/103037333
大括号
$\left\{ \begin{aligned}
\boldsymbol{w}^T\boldsymbol{x}+b \geqslant +1,& & y_i=+1\\
\boldsymbol{w}^T\boldsymbol{x}+b \leqslant -1,& & y_i=-1 \\
\end{aligned} \right.$
ℓ \ell ℓ的打法
$\ell$