Transformer:注意力机制(attention)和自注意力机制(self-attention)的学习总结
目录
- 前言
- 1. 注意力机制
-
- 1.1非自主提示和自主提示
- 1.2 查询,键和值
- 1.3 注意力机制的公式
-
- 1.3.1 平均汇聚
- 1.3.2 非参数的注意力汇聚(Nadaraya-Watson核回归)
- 1.3.3 带参数的注意力汇聚(Nadaraya-Watson核回归)
- 1.4 注意力机制的评分函数( a ( q u e r y , k e y ) a(query, key) a(query,key))
-
- 1.4.1 加性注意力
- 1.4.2 点积注意力
- 1.5 多头注意力(multi-head)
- 2. 自注意力机制
-
- 2.1 优缺点
- 2.2单一自注意力机制图片示例
- 2.3 多头自注意力机制图片示例
- 总结
前言
由于我对注意力机制和自注意力机制的原理和区别不是很清楚。因此,对相关内容进行了深入学习。在阅读多个博客后,我自己总结出了本篇文章,分享给各位读者朋友。由于我才疏学浅,如果理解有偏差,则望各位读者朋友及时指出。 ⌣ ¨ \ddot\smile ⌣¨
本文主要分为两个部分:
第一部分重点介绍了注意力机制的原理、公式演变、评分函数以及多头注意力。
第二部分重点介绍了自注意力机制的原理、优缺点以及和注意力机制的区别,并最后给出了单头和多头自注意力机制的图片示例。
建议顺序阅读,也可以在目录中选择感兴趣的章节
本文的参考博客如下,其中大部分理解来自于动手学深度学习的注意力机制部分。如果读者在阅读完本文后仍不理解,可以阅读该资料,细节方面会更多。
参考资料:
1.动手学深度学习
2.作者:张俊林,深度学习中的注意力机制(2017版)
3.作者:太阳花的小绿豆,self_attention和mutil self_attention的原理
1. 注意力机制
注意力机制其实是源自于人对于外部信息的处理能力。由于人每一时刻接受的信息都是无比的庞大且复杂,远远超过人脑的处理能力,因此人在处理信息的时候,会将注意力放在需要关注的信息上,对于其他无关的外部信息进行过滤,这种处理方式被称为注意力机制。
1.1非自主提示和自主提示
针对于注意力机制的引起方式,可以分为两类,一种是非自主提示,另一种是自主提示。其中非自主提示指的是由于物体本身的特征十分突出引起的注意力倾向,自主提示指的是经过先验知识的介入下,对具有先验权重的物体引起的注意力倾向。换句话说,可以理解为非自主提示源自于物体本身,而自主提示源自于一种主观倾向。举例说明如下:

当我们第一眼看到上图时,我们便会首先将注意力集中到兔子身上。这是因为,整张图中兔子的特征十分的突出,让人一眼就关注到兔子身上。这种引起注意力的方式便是非自主提示。在看到兔子之后,我们便想兔子在干嘛,从而我们就会关注兔子的行为。此时兔子在吃草,这时我们便把注意力集中在兔子周边的草上。这种引起注意力机制的方式便是自主提示,其中"兔子在干嘛"则是我们主观意识。
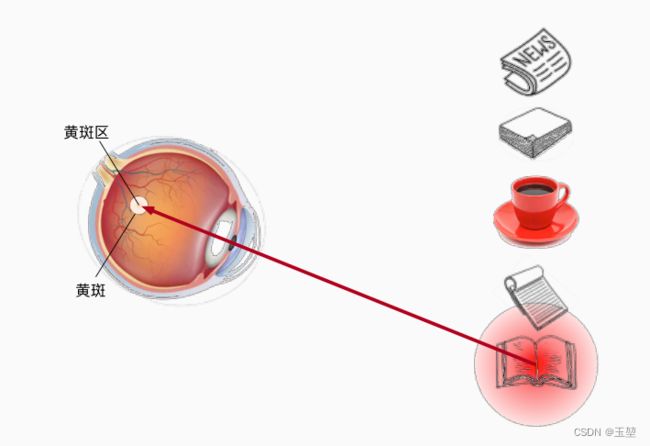
另外,为加深理解,再引用一下动手学深度学习中的例子解释:
此时我们面前有五个物体,分别是报纸,论文,咖啡,笔记本和书。首先,我们会关注在咖啡身上,因为只有咖啡是红色,而其他物体是黑白。那么红色的咖啡由于其显眼的特征,就成了注意力机制的非自主提示。

喝完咖啡后,十分精神,想看本书。此时,通过"想看书"这种意识,我们将注意力放到了书上。这种通过主观意识引起注意力的方式称为自主提示。
1.2 查询,键和值
根据自主提示和非自主提示来设计注意力机制。首先考虑简单情况,即只考虑非自主提示的话,只需要对所有物体的特征信息(非自主提示)进行简单的全连接层,甚至是无参数的平均汇聚层或者最大汇聚层,就可以提取出需要感兴趣的物体。
下图是平均汇聚方法的示例图,最后结果是所有物体向量的平均加权和。

而如果考虑自主提示的话,我们就需要设计一种通过查询(Query),键(Key)和值(Value) 来实现注意力机制的方法。其中Query指的是自主提示,即主观意识的特征向量,Key指的是非自主提示,即物体的突出特征信息向量,Value则是代表物体本身的特征向量。
注意力机制是通过Query与Key的注意力汇聚(指的是对Query和Key的相关性进行建模,实现池化筛选或者分配权重),实现对Value的注意力权重分配,生成最终的输出结果。如下图所示:

另外,还有一种理解方式。我们可以将查询,键和值理解为一种软寻址(Soft Addressing)
Value可以看作存储器存储的内容,Key看作是存储器的地址。当Key==Query时,则取出Key地址对应存储器中的Value值,这被称为硬寻址。而软寻址则是通过计算Key和Query的相似度来进行寻址,这种方法不只是获取一个Key地址中存储器的Value值,而是获取所有的存储器中的Value值的加权和 。至于每个Value的权重(重要程度),是通过Key和Query相似度计算得到的,最终的输出是所有Value值和其权重的加权和。如下图所示:

1.3 注意力机制的公式
假设有一组数据训练数据 { [ x 1 , y 1 ] , [ x 2 , y 2 ] . . . [ x 50 , y 50 ] } \{[x_1,y_1],[x_2,y_2]...[x_{50}, y_{50}]\} {[x1,y1],[x2,y2]...[x50,y50]}。我们需要通过这些数据训练出一个函数 f f f,从而满足 y i = f ( x i ) , i = 1 , 2 , 3...50 y_i=f(x_i),i=1,2,3...50 yi=f(xi),i=1,2,3...50。先假定函数 f f f为 s i n sin sin函数。本示例的目的是通过训练数据 { [ x 1 , y 1 ] , [ x 2 , y 2 ] . . . [ x 50 , y 50 ] } \{[x_1,y_1],[x_2,y_2]...[x_{50}, y_{50}]\} {[x1,y1],[x2,y2]...[x50,y50]}拟合出这个 s i n sin sin函数。
先通过python代码生成一组训练数据,生成方法如下公式:
y = s i n ( x ) 2 + x 0.8 + ϵ y=sin(x)^2+x^{0.8}+\epsilon y=sin(x)2+x0.8+ϵ
import numpy as np
import matplotlib.pyplot as plt
from learn_attention_pool import CE, AttentionPoolWithParameter
import torch
import copy
def f(x):
"""
通过 y=sin(x)^2+x^0.8+\epsilon 获取所需的训练数据。
:param x:训练数据x, 类型numpy(dim,)
:return: 训练标签y, 类型numpy(dim,)
"""
return np.sin(x)*2 + x**0.8
def main():
# ----------------------------------------------------------------------
# 生成数据
# ----------------------------------------------------------------------
# 生成训练数据和标签。
x_train = np.sort(np.random.rand(50)) * 6
y_train = f(x_train) + np.random.normal(0, 0.5, 50)
# 生成测试数据和真实标签。
x_test = np.arange(0, 6.28, 0.12566)
y_true = f(x_test)
# 绘制图像
plt.figure(1)
l1 = plt.scatter(x_train, y_train, color="r")
l2, = plt.plot(x_test, y_true, color="b")
plt.legend(handles=[l1, l2], labels=["train_data", "sin_function"], loc="best")
plt.savefig("data.png")
为了防止混淆,专门解释下:
训练数据:x_train, y_train是需要拟合的数据,
真实标签:y_true是我们想要的结果。
测试数据:x_test是测试x_train, y_train拟合出来的函数 f f f效果的数据。
上图中红点表示训练数据,蓝色的线表示我们想要拟合的函数。
1.3.1 平均汇聚
获得数据后,先使用平均汇聚方法来解决回归问题: 基于平均汇聚来计算所有训练样本输出值的平均值,公式如下:
f ( x ) = 1 n ∑ i = 1 n y i , i = 1 , 2 , 3...50 f(x)=\frac{1}{n}\sum^n_{i=1}y_i,i=1,2,3...50 f(x)=n1∑i=1nyi,i=1,2,3...50
def average_pool(y_train):
"""
平均汇聚层,实现 f(x)=\frac{1}{n}\sum^n_{i=1}y_i
:param y_train:输入数据y_train,类型numpy(dim,)
:return:numpy(公式的输出值 * dim),类型numpy(dim,)
"""
return np.array([np.sum(y_train)/len(y_train)]*len(y_train))
# ----------------------------------------------------------------------
# 平均汇聚方法
# ----------------------------------------------------------------------
average_function = average_pool(y_train)
l3, = plt.plot(x_train, average_function, color="g")
plt.legend(handles=[l1, l2, l3], labels=["train_data", "sin_function", "average_function"], loc="best")
plt.savefig("average_function.png")
结果如下:
绿线是平均汇聚的结果,从图中可以看出,平均汇聚的方法效果很差。
1.3.2 非参数的注意力汇聚(Nadaraya-Watson核回归)
很显然,平均汇聚方法只考虑 y i y_i yi,为了获取更好的效果还可以考虑 x i x_i xi。于是Nadaraya [Nadaraya, 1964]和 Watson [Watson, 1964]提出了一个方法,根据输入的位置对输出进行加权。公式如下:
f ( x ) = ∑ i = 1 n K ( x , x i ) ∑ j = 1 n K ( x , x j ) y i f(x)=\sum^n_{i=1}\frac{K(x,x_i)}{\sum^n_{j=1}K(x, x_j)}y_i f(x)=∑i=1n∑j=1nK(x,xj)K(x,xi)yi
其中 K ( x , x i ) K(x,x_i) K(x,xi)是核函数,所以,该方法也成为Nadaraya-Watson核回归。上述公式还可以写成一个更加通用形式来描述注意力机制,公式如下。
f ( x ) = ∑ i = 1 n a ( x , x i ) y i f(x)=\sum^n_{i=1}a(x, x_i)y_i f(x)=∑i=1na(x,xi)yi
其中 a ( x , x i ) a(x, x_i) a(x,xi)就是下一章节所介绍的评分函数,其作用是对查询和键的关系进行建模,生成注意力权重,即attention值,用来描述查询和键的相似程度。
为了进一步的理解非参数的注意力汇聚,本示例选取高斯核作为核函数。高斯核函数如下公式所示:
K ( μ ) = 1 2 π e x p ( − μ 2 2 ) K(\mu) =\frac{1}{\sqrt{2\pi}}exp(-\frac{\mu^2}{2}) K(μ)=2π1exp(−2μ2)
将该核函数带入注意力汇聚公式中,得到下式:
f ( x ) = ∑ i = 1 n e x p ( − 1 2 ( x − x i ) 2 ) ∑ j = 1 n e x p ( − 1 2 ( x − x j ) 2 ) y i = ∑ i = 1 n s o f t m a x ( e x p ( − 1 2 ( x − x i ) 2 ) ) y i f(x)=\sum^n_{i=1}\frac{exp(-\frac{1}{2}(x-x_i)^2)}{\sum^n_{j=1}exp(-\frac{1}{2}(x-x_j)^2)}y_i=\sum^n_{i=1}softmax(exp(-\frac{1}{2}(x-x_i)^2))y_i f(x)=∑i=1n∑j=1nexp(−21(x−xj)2)exp(−21(x−xi)2)yi=∑i=1nsoftmax(exp(−21(x−xi)2))yi
通过python代码实现该方法:
#使用到的方法
def softmax(x):
"""
计算softmax值
:param x: 输入数据x, 类型numpy(dim,)
:return: softmax值, 类型numpy(dim,)
"""
return np.exp(x)/np.sum(np.exp(x))
def attention_pool(query_x, key, value):
"""
非参数的注意力汇聚层的实现方法。
$f(x)=\sum^n_{i=1}softmax(exp(-\frac{1}{2}(x-x_i)^2))y_i$
:param query_x:查询, 类型numpy(dim,)
:param key:键,类型numpy(dim,)
:param value:值,类型numpy(dim,)
:return: 注意力汇聚的加权和,类型numpy(dim)。query_x中的元素,都是该元素通过该计算key的权重,和value的加权和。
"""
for i in range(len(value)):
query_x[i] = np.sum(np.dot(softmax(-(query_x[i] - key)**2/2), value))
return query_x
def show_heapmap(query_x, x_train):
"""
计算注意力机制图。
:param query_x: 查询, 类型numpy(dim,)
:param x_train: 键, 类型numpy(dim,)
:return:注意力机制图,类型numpy(dim, dim)
"""
heapmap = []
for i in range(len(x_train)):
heapmap.append(softmax(-(query_x[i] - x_train)**2/2))
heapmap = np.array(heapmap)
return heapmap
# ----------------------------------------------------------------------
# 非参数的注意力汇聚方法
# ----------------------------------------------------------------------
query_x = copy.deepcopy(x_test)
sf_attebtiob_function = attention_pool(query_x, x_train, y_train)
l4, = plt.plot(x_train, sf_attebtiob_function, color="black")
plt.legend(handles=[l1, l2, l3, l4], labels=["train_data", "sin_function", "average_function", "sf_attention_function"], loc="best")
plt.savefig("sf_average_function.png")
# plt.show()
# 生成注意力机制图。
heap_map = show_heapmap(x_test, x_train)
plt.figure(2)
plt.imshow(heap_map)
plt.xlabel("x_train")
plt.ylabel("query_x")
plt.savefig("heapmap_no_param.png")
结果如下图所示:

黑色的线是非参数注意力汇聚方法的结果,从上图可以看出其结果明显优于平局汇聚方法。
下图是注意力权重图。表示横轴Key和纵轴Query的权重关系,可以看出Query和Key值相似时,权重很大,其他情况权重很小。如下图所示:

1.3.3 带参数的注意力汇聚(Nadaraya-Watson核回归)
非参数的Nadaraya-Watson核回归具有一致性(consistency)的优点: 如果有足够的数据,此模型会收敛到最优结果。 但是,我们也可以使用带参数的方法更好,更快的拟合目标函数。公式如下所示,其中 w w w是可学习的参数。
f ( x ) = ∑ i = 1 n e x p ( − 1 2 ( ( x − x i ) w ) 2 ) ∑ j = 1 n e x p ( − 1 2 ( ( x − x j ) w ) 2 ) y i = ∑ i = 1 n s o f t m a x ( e x p ( − 1 2 ( ( x − x i ) w ) 2 ) ) y i f(x)=\sum^n_{i=1}\frac{exp(-\frac{1}{2}((x-x_i)w)^2)}{\sum^n_{j=1}exp(-\frac{1}{2}((x-x_j)w)^2)}y_i=\sum^n_{i=1}softmax(exp(-\frac{1}{2}((x-x_i)w)^2))y_i f(x)=∑i=1n∑j=1nexp(−21((x−xj)w)2)exp(−21((x−xi)w)2)yi=∑i=1nsoftmax(exp(−21((x−xi)w)2))yi
实现代码如下:
#使用的网络和损失
import torch
import torch.nn as nn
class AttentionPoolWithParameter(nn.Module):
"""
带参数的注意力汇聚实现方法
"""
def __init__(self):
super(AttentionPoolWithParameter, self).__init__()
# 可学习的参数w。
self.w = nn.Parameter(torch.rand((1,), requires_grad=True))
def forward(self, q:"(1, 50)", k:"(1, 50)", v:"(1, 50)"):
"""
实现方法。
:param q: 查询, tensor(1,dim)
:param k: 键, tensor(1,dim)
:param v: 值, tensor(1,dim)
:return: 注意力权重和值的加权和, tensor(1,dim)
"""
#通过复制将q的维度,扩展为(dim,dim),方便计算
q = q.repeat_interleave(k.shape[1]).reshape(-1, k.shape[1])
attention = torch.softmax(-((q - k) * self.w)**2/2, dim=1)
# torch.bmm是矩阵相乘.
return torch.bmm(attention.unsqueeze(0), v.unsqueeze(-1)).reshape(1, -1)
class CE(nn.Module):
def __init__(self):
super(CE, self).__init__()
self.loss = nn.MSELoss(reduction='none')
def forward(self, pred, y_true):
return self.loss(pred, y_true)
#训练代码:
# ----------------------------------------------------------------------
# 带参数的注意力汇聚方法
# ----------------------------------------------------------------------
net = AttentionPoolWithParameter()
optimizer = torch.optim.SGD(net.parameters(), lr=0.5)
loss = CE()
x_test = torch.tensor(x_test.astype(np.float32)).reshape(1, -1)
y_true = torch.tensor(y_true.astype(np.float32)).reshape(1, -1)
x_train = torch.tensor(x_train.astype(np.float32)).reshape(1, -1)
y_train = torch.tensor(y_train.astype(np.float32)).reshape(1, -1)
net.train()
for epoch in range(50):
optimizer.zero_grad()
y_pred = net(x_test, x_train, y_train)
l = loss(y_pred, y_true)
l.sum().backward()
optimizer.step()
print(f'epoch {epoch + 1}, loss {float(l.sum()):.6f}')
print(net.w)
net.eval()
with torch.no_grad():
y_pred = net(x_test, x_train, y_train)
plt.figure(1)
l5, = plt.plot(x_test.squeeze(), y_pred.squeeze(), color="pink")
plt.legend(handles=[l1, l2, l3, l4, l5],
labels=["train_data", "sin_function", "average_function",
"sf_attention_function", "sf_attention_with_params_function"], loc="best")
plt.savefig("sf_average_with_params_function.png")
heap_map = show_heapmap(x_test.squeeze().numpy(), y_pred.squeeze().numpy())
plt.figure(3)
plt.imshow(heap_map)
plt.xlabel("x_train")
plt.ylabel("query_x")
plt.savefig("heapmap_param.png")
plt.show()
拟合结果和注意力权重图如下所示:


粉色是带参数注意力汇聚方法的拟合效果,显然该效果远远好于之前的方法。之所有乘以一个 w w w参数效果这么好,个人理解是, w w w参数可以放大键和查询的差距,使得经过 e x p exp exp函数后,键和查询相关性差的权重越小,相关性好的权重越大。再经过softmax后,使attention值变得更具有区分性。
总结:
- Nadaraya-Watson核回归是具有注意力机制的机器学习范例。
- Nadaraya-Watson核回归的注意力汇聚是对训练数据中输出的加权平均。从注意力的角度来看,分配给每个值的注意力权重取决于将值所对应的键和查询作为输入的函数。
- 注意力汇聚可以分为非参数型和带参数型。
最后,经过上述几个例子。我们可以总结出一个通用的注意力机制公式:
f ( x ) = ∑ i = 1 n a ( q u e r y , k e y i ) v a l u e i , i = 1 , 2 , 3... n f(x)=\sum^n_{i=1}a(query, key_i)value_i ,i=1,2,3...n f(x)=∑i=1na(query,keyi)valuei,i=1,2,3...n
其中的 a ( q u e r y , k e y i ) a(query, key_i) a(query,keyi)称为评分函数。用来对查询和键的关系进行数学建模,即实现查询和键的相关性计算,然后再经过 s o f t m a x softmax softmax函数,即可得到查询和键的概率分布(即注意力权重)。最后,通过注意力权重和Value值进行加权,实现注意力分配或者结果筛选。
1.4 注意力机制的评分函数( a ( q u e r y , k e y ) a(query, key) a(query,key))
a ( q u e r y , k e y i ) a(query, key_i) a(query,keyi)作为评分函数可以分为两种,分别是加性注意力和点积注意力。
1.4.1 加性注意力
加性注意力机制一般是来处理Query和Key的向量维数不一致的情况,公式如下:
a ( q , k ) = W v T t a n h ( W q q + W k k ) a(q, k)=W_v^Ttanh(W_qq+W_kk) a(q,k)=WvTtanh(Wqq+Wkk)
假设, q ∈ R q q\in R^{q} q∈Rq, k ∈ R k k\in R^{k} k∈Rk, 则 W q ∈ R h × q W_q\in R^{h\times q} Wq∈Rh×q, W k ∈ R h × k W_k\in R^{h\times k} Wk∈Rh×k, W v ∈ R h × v W_v\in R^{h\times v} Wv∈Rh×v。通过两个全连接层可以将查询和键都统一到一个向量维度,然后经过相加和激活函数tanh,即可得到查询和键的关系,再经过全连接层 W v W_v Wv来将向量维数统一到和Value的向量维度一致。
最后结果再经过 s o f t m a x softmax softmax函数,可以得到查询和键的概率分布(注意力权重)。公式如下:
s o f t m a x ( W v T t a n h ( W q q + W k k ) ) softmax(W_v^Ttanh(W_qq+W_kk)) softmax(WvTtanh(Wqq+Wkk))
个人理解:
可以从向量相加来理解,当向量 q q q和向量 k k k越接近,两个向量相加的结果就越大,那么加性注意力获得的权重就越大,反之两个向量离的越远则相加的结果越小,加性注意力获得的权重就会越小。
1.4.2 点积注意力
点积注意力相比于加性注意力,其计算效率更高,但是必须要Query和Key的向量维数一致。其公式如下:
a ( q , k ) = q T ⋅ k d a(q, k)=\frac{q^T\cdot k}{\sqrt{d}} a(q,k)=dqT⋅k
其中 q ∈ R n × d q\in R^{n\times d} q∈Rn×d, k ∈ R m × d k\in R^{m\times d} k∈Rm×d。然后再经过 s o f t m a x softmax softmax函数获取权重的概率分布(注意力权重)。公式如下:
s o f t m a x ( Q T K d ) softmax(\frac{Q^TK}{\sqrt{d}}) softmax(dQTK)
动手学深度学习资料中对于除以 d \sqrt{d} d的解释:
假设查询和键的所有元素都是独立的随机变量, 并且都满足零均值和单位方差, 那么两个向量的点积的均值为0,方差为1。 为确保无论向量长度如何, 点积的方差在不考虑向量长度的情况下仍然是1, 我们将点积除以 d \sqrt{d} d。
而我之前的理解是为了防止数值过大,从而使softmax的输出过大,区分不开
个人理解:
我会从点积公式上理解,点积公式为 A → ⋅ B → = ∣ A ∣ ∣ B ∣ c o s ( θ ) \mathop{A}\limits ^{\rightarrow}\cdot \mathop{B}\limits ^{\rightarrow} =|A||B|cos(\theta) A→⋅B→=∣A∣∣B∣cos(θ)。从公式中可以看出如果两个向量越近,则 c o s ( θ ) cos(\theta) cos(θ)越大,点积值越大。因此,注意力的权重就越大。反之,如果两个向量离的越远,则 c o s ( θ ) cos(\theta) cos(θ)越小,点积值越小,从而注意力的权重就越小。
1.5 多头注意力(multi-head)
单一注意力汇聚,只会建立一种查询和键的依赖关系。而我们常希望可以基于相同的注意力汇聚方法学习到不同的依赖关系,然后将这些依赖关系组合起来,实现捕获序列内各种范围的依赖关系。例如,机器翻译任务,以 " I like fishing because it can relax my mind " 要翻译为 " 我喜欢钓鱼,因为可以放松心灵 " 为例,我们以"放松"为Query,对英文句子中每个单词的Key进行注意力汇聚,结果获取"放松"和"relax"的依赖关系。这是单头注意力的结果,如果我们进行多次注意力汇聚,则可能捕获"放松"和"fishing", "I"等单词的依赖关系。这样,我们将多个结果进行融合就可以得到更为全面,复杂的依赖关系,这对于深度学习下游任务,例如目标检测,语义分割等都具有很大帮助。这就是本章节要介绍的多头注意力汇聚方法。具体流程如下:
- 首先,将查询,键和值通过多组全连接层来获取对应的特征向量。由于每个全连接层的参数都是可学习的,因此,经过独立学习可以获取多组不同特征的查询,键和值的特征向量。
- 然后,对多组查询,键和值的特征向量进行注意力汇聚,从而获得多个不同注意力汇聚运算结果。
- 最后,将所有的注意力汇聚运算结果进行拼接,再经过一个全连接层,就可以映射出所需的最后输出。
其中每一个注意力汇聚都被称作一个头(head)。由于有多个注意力汇聚,因此才被称为多头注意力。
2. 自注意力机制
自注意力机制和注意力机制的区别就在于,注意力机制的查询和键是不同来源的,例如,在Encoder-Decoder模型中,键是Encoder中的元素,而查询是Decoder中的元素。在中译英模型中,查询是中文单词特征,而键则是英文单词特征。而自注意力机制的查询和键则都是来自于同一组的元素,例如,在Encoder-Decoder模型中,查询和键都是Encoder中的元素,即查询和键都是中文特征,相互之间做注意力汇聚。也可以理解为同一句话中的词元或者同一张图像中不同的patch,这都是一组元素内部相互做注意力机制,因此,自注意力机制(self-attention)也被称为内部注意力机制(intra-attention)。
个人理解:
自注意力机制的作用是学习Query对其他所有Key的依赖关系。即每个特征信息都是组内其他所有特征信息的关系组合。
举例说明:在一句话中,通过自注意力机制可以使每个单词不光包含自己的主体信息,还会包含和其他单词的关系信息(主谓,指代等)。因此,每个单词都具备和其他所有单词的依赖关系。再从图像中来讲,就是每个patch(图像会划成不同的块,每个块称为patch)都包含有其他patch的关系信息。其实也可以理解为建立了全局感受野。还有一个例子就是HRNetV2_OCR网络模型中的OCR模块(OCR,目标上下文表示),通过OCR模块可以使每个像素都具有和所有类别的依赖关系,具体内容可以参考我的另一篇博客Segmentation:HRnetv2+OCR 个人总结中的OCR部分。
2.1 优缺点
同样是个人理解,在看了一些博客和视频后,总结如下。
以在图像中为例:
优点:可以建立全局的依赖关系,扩大图像的感受野。相比于CNN,其感受野更大,可以获取更多上下文信息。(在另一篇我的博客Transformer:SegFormer个人总结中介绍了该论文作者通过实验论证了自注意力机制比卷积可以获得更大的感受野,这对于语义分割任务十分有效)。
缺点:自注意力机制是通过筛选重要信息,过滤不重要信息实现的,这就导致其有效信息的抓取能力会比CNN小一些。这所以这样是因为自注意力机制相比CNN,无法利用图像本身具有的尺度,平移不变性,以及图像的特征局部性(图片上相邻的区域有相似的特征,即同一物体的信息往往都集中在局部)这些先验知识,只能通过大量数据进行学习。这就导致自注意力机制只有在大数据的基础上才能有效地建立准确的全局关系,而在小数据的情况下,其效果不如CNN。
2.2单一自注意力机制图片示例
假设,对deep learning这个词组做单头的自注意力机制,原理示例如下图所示:

注意:
- 向量 a a a是Deep单词经过全连接层 W a W_a Wa得到的,向量 b b b是Learning单词经过全连接层 W b W_b Wb得到的。
- 向量 q 1 , q 2 q_1, q_2 q1,q2分别是向量 a , b a, b a,b经过全连接层 W q W_q Wq得到的。 k 1 , k 2 , v 1 , v 2 k_1, k_2, v_1, v_2 k1,k2,v1,v2同理。
- 向量 a ′ , b ′ a{'}, b{'} a′,b′分别是向量 a , b a, b a,b经过注意力汇聚后的结果。
2.3 多头自注意力机制图片示例
假设,对deep learning这个词组做多头的自注意力机制(下图是以两头为例),原理示例如下图所示:

总结
本文内容总结如下:
- 注意力可以分为两种方式分别是自主提示和非自主提示。其中非自主提示是键,自主提示是查询,物体原始向量是值。键和值是一一对应的。
- 注意力机制的评分函数可以对查询和键进行关系建模,获取查询和键的相似度匹配。其方法分为两种:加性注意力和点积注意力。常用的是点积注意力。
- 如果查询和键是同一组内的特征,并且相互做注意力机制,则称为自注意力机制或内部注意力机制。
- 多头注意力机制的多头表示对每个Query和所有的Key-Value做多次注意力机制。做两次,就是两头,做三次,就是三头。这样做的意义在于获取每个Query和所有的Key-Value的不同的依赖关系。
- 自注意力机制的优缺点简记为【优点:感受野大。缺点:需要大数据。】
最后如果您觉得对您有帮助的话,可以给小弟一个赞。 ⌣ ¨ \ddot\smile ⌣¨

