聚类分析与SPSS实现——《社会统计分析方法》

目录

一、定义

二、常用的聚类分析方法

三、主要步骤

四、相似性测度

五、聚类方法及SPSS操作​​​​​​​​​​​​​​

(一)层次聚类法(hierarchical cluster procedures)

(二)迭代聚类法(K-均值聚类)

​​​​​​​(三)二阶聚类法(Two Step)

六、聚类方法的选择

七、聚类结果的解释和证实

八、注意事项​​​​​​​

---

一、定义

        根据研究对象的特征对研究对象进行分类，使得同一类个体之间有高度的同质性，不同类的个体之间有较高的异质性。

        聚类分析是一种探索性的分析，在分类的过程中，人们不必事先给出一个分类的标准，聚类分析能够从样本数据出发，自动进行分类。聚类分析所使用方法的不同，常常会得到不同的结论。不同研究者对于同一组数据进行聚类分析，所得到的聚类数未必一致。

        从实际应用的角度看，聚类分析是数据挖掘的主要任务之一。而且聚类能够作为一个独立的工具获得数据的分布状况，观察每一簇数据的特征，集中对特定的聚簇集合作进一步地分析。聚类分析还可以作为其他算法（如分类和定性归纳算法）的预处理步骤。

聚类分析在SPSS26中的位置：“分析”——“分类”，再选择相应的聚类方法即可。

二、常用的聚类分析方法

聚类方法	聚类对象	变量类型	分类数	样本容量
系统聚类	个案或变量	连续或分类	固定分类或指定范围	<200
K-均值聚类	个案	连续	固定分类数	大样本
二阶聚类	个案或变量	连续或分类	系统自动确定	大样本

三、主要步骤

1. 根据研究目的选择合适的聚类变量
2. 计算相似性测度
3. 选定聚类方法进行聚类
4. 对结果进行解释和验证

四、相似性测度

为了克服变量测度单位的影响，在计算相似测度之间，一般要对变量标准化处理。

1.相关测度应用最广泛的是皮尔逊相关系数(Person correlation)，更大程度上反映了案例在聚类变量上变化模式的相似性，变量值大小差异对其影响不大，也被称为形状测度。

2.距离测度：在m维空间中定义点和点的距离，距离越近的点，相似程度越高，聚类时更可能归为一类。明可夫斯基距离是通用的距离测度公式 。

3.关联测度：度量聚类变量为分类变量的研究对象的相似性。

(1)简单匹配系数：只用于二分变量，两个案例在所有的聚类变量上答案相同的情况。举个例子，我们用1代表“是”，0代表“否”，如果两个案例都回答1的次数为a，都回答0的次数为b，回答不同的次数为c+d(两个案例分别回答1和0)，则简单匹配系数为：

​​​​​​​

(2)Jaccard系数：只用于二分变量，简单匹配系数类似，但只保存都回答“是”的部分：

​​​​​​​ 

(3)Gower系数：允许聚类变量可以是名义变量、序次变量和间距测度变量

       其中，为案例i和j在变量k上的相似性得分，为加权变量

       对于间距测度或以上的变量: 

       其中，是变量k的全距，即变量k的最大值与最小值的差

五、聚类方法及SPSS操作​​​​​​​​​​​​​​

(一)层次聚类法(hierarchical cluster procedures)

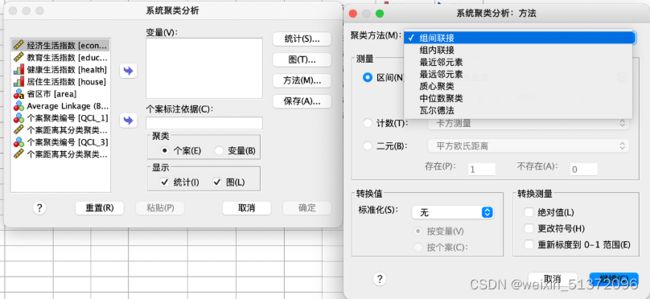
SPSS窗口：

此处选择四个指数为聚类分析的变量，“省市区”作为个案标准依据。因为我们想对地区进行聚类，所以在“聚类”选项选择“个案”。如果在其他案例中，是对表征同一对象不同特征的变量进行聚类，则选择“变量” 。

    基本思想：通过某种相似性测度计算节点之间的相似性，并按相似度由高到低排序，逐步重新连接个节点。

    方法：

1. 最短聚类法：把两个类之间的距离定义为一个类中的所有案例与另一类中的所有案例之间的距离最小者
2. 最长聚类法：把类与类之间的距离定义为两类中离得最远的两个案例之间的距离​​​​​​​
3. 平均联结法——使用最广泛
   1. 组内联结：在计算距离时把两组所有个案之间的距离都考虑在内
   2. 组间联结：只考虑两类之间个案之间的距离的平均，是SPSS中的默认设置
4. 矩心法：把两类之间的距离定义为两类矩心之间的距离，每一类的矩心是该类中所有案例在各个变量上的均值代表的点
5. 瓦尔德法(离差平方和法)：基本思想是同一类内案例的离差平方和应该比较小，不同类之间案例的离差平方和应该较大

聚类结果的表示：  

1. 聚类进度表：第一列表示聚类的顺序，第二、三列表示每一步将哪两列合并，新合并的类的序号取两类中最小的；第四列表示被合并的两类之间的距离，也称为聚合系数(fusion coefficient)，第五、六列表示被合并的两类上一次合并是在哪一步形成的。

2. 冰柱图

       纵向冰柱图：水平方向表示案例，竖直方向表示类数

       比如，最高的冰柱只到1，表示水平1一下所有案例为一类；而在水平2以下，此唯一的冰柱把案例分成两类。在水平3上则有两个冰柱，以它们为界把案例分为3类。具体来看第一步，案例1和案例13聚为1类，对应的分类数是29；第二步，  案例27和28聚为一 类，对应的分类数是28；每一步减少一类，直到所有案例归为一类。​​​​​​​​​​​​​​

(二)迭代聚类法(K-均值聚类)

 SPSS窗口： 

在“迭代”窗口中，我们可以设置迭代的终止条件，即到达设定的最大值后将停止迭代分析，输出聚类分析结果；

​​​​​​​收敛性标准设置的是凝聚点改变的最大距离小于初始凝聚点的比例，小于设定值时，也会停止迭代，输出结果；

使用运行均值表示每次观测后都重新计算凝聚点，这些设置保持默认即可。

在“选项”窗口中，可以选择输出“初始聚类中心”“ANOVA表”(方差分析表)、“每个个案的聚类信息”。

注意：由于类别选择就是为了使得类别中心之间的差别最大化，因此ANOVA表中的F值和显著性水平不能作为各聚类平均值是否相等的常规假设检验概率来理解。​​​​​​​

​​​​​​​基本思想：先随机选取K个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了，每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。

步骤：

1. 指定要形成的聚类数，对样本进行初始分类并计算每一类的中心
2. 调整分类。计算每个样本到各类中心店的距离，把每个样本点归入距中心最近的那一类
3. 重新计算每一类的中心
4. 重复上述两步，直到没有样本点可以调整为止

(三)二阶聚类法(Two Step)

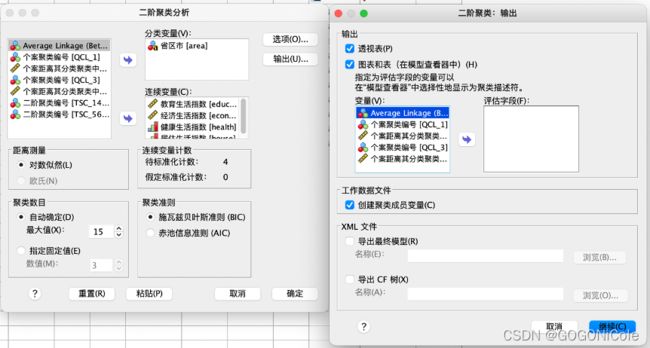
SPSS窗口

    基本思想：以个案或变量间的距离为依据形成相应的聚类特征树结点来构造聚类特征树，再通过信息准则确定最优分组个数对各个节点进行分组。

    优点：

1. 能同时处理分类变量和连续变量
2. 可自动选择最优的分类个数
3. 适用于大样本数据

    分类数的确定准则：

1. 任何类都必须是在各邻近类中最突出的，即各中心之间距离必须大
2. 各类包含的元素不要过多
3. 分类数目应该符合使用的目的
4. 若采用几种不同的聚类方法处理，则在各自的聚类图上应发现相同的类​​​​​​​

六、聚类方法的选择

     选择依据：

1. 类的结构(主要指类的形状、规模和个数)
2. 异常值的存在，层次聚类法受影响比较大
3. 类与类之间重叠的程度
4. 相似程度的选择

注意：

1. 层次聚类法受异常值的影响比较大
2. 迭代聚类法对初始分类非常敏感，而且只能得到局部最优解
3. 迭代聚类法只能对个案间的聚类，只能对连续变量进行聚类

七、聚类结果的解释和证实

       在“统计(S) ”窗口可以选择输出聚类计划表(A)，距离矩阵(P)以及聚类成员，即每个案例属于那一类，“单个解”输出制定类数的聚类结果，“解的范围”输出制定类数范围的聚类结果，如指定2-4，则输出聚2、3、4类的聚类结果。

不同的聚类方法的结果是不稳定的。通常的做法是把样本分成两组，分别做聚类分析，对结果进行比较，或者对同一数据采用不同的方法反复聚类。

八、注意事项​​​​​​​

1. 选择的聚类指标能代表研究对象

聚类分析的基础依据是比较研究主题的特征/性质的差异性，而特征/性质则以数量化的指标来表达。因此，做好聚类分析的关键前提，是要选对能很好地代表、衡量研究主题特征的指标。

比如，希望依照学校的科研情况对高校进行分类，那就可以选择参加科研人数、科研经费、立项课题数等变量指标作为聚类指标，而不应该选择如在校人数、校园面积、年用水量等和研究主题无关的指标。

2. 对数据进行标准化处理

由于聚类分析主要是基于个案或变量之间的距离或者相似性，要保证可比性，就要求数据无量纲差异（如数量级、单位上的差异），能够在同一标准下进行比较。因此，在聚类分析前，需要对数据进行处理，将原始数据转化为无量纲的数据。常用的转化方法有：

（1）转化为同标准的标准分：标准化处理是最常用的方法之一

（2）用变量值除以全距（最大值减去最小值）

（3）变量值减去最小值再除以全距

（4）变量值除以最大值

3. 聚类指标之间不应有较强的线性相关关系

聚类分析是以各种距离来度量个案间或变量间的亲疏程度。如果所选的聚类变量指标之间存在较高的线性关系，能够相互替代，那么计算距离时同类变量将会重复起作用，将在距离中有较高的权重，从而导致聚类结果偏向该变量。

此部分来源：https://zhuanlan.zhihu.com/p/397631854​​​​​​​

本文章数据来源：郭志刚《社会统计分析方法——SPSS软件应用》配套数据