概率扩散模型(Denoising Diffusion Probabilistic Models)基本原理
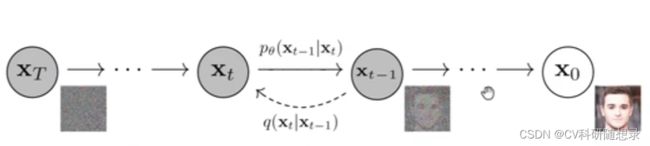
不妨设 x 0 ∼ q X ( x 0 ) \mathrm{x}^{0} \sim q_{\mathcal{X}}\left(\mathrm{x}^{0}\right) x0∼qX(x0) 是从输入空间 X = R D \mathcal{X}=\mathbb{R}^{D} X=RD 采样而来的样本,且用概率密度分布函数 p θ ( x 0 ) p_{\theta}(\mathrm{x}^{0}) pθ(x0) 来逼近真实分布 q X ( x 0 ) q_{\mathcal{X}}(\mathrm{x}^{0}) qX(x0)。Diffusion Model 是一个包含隐变量的生成式模型 p θ ( x 0 ) : = ∫ p θ ( x 0 : N ) d x 1 : N p_{\theta}\left(\mathbf{x}^{0}\right):=\int p_{\theta}\left(\mathbf{x}^{0: N}\right) \mathrm{d} \mathbf{x}^{1: N} pθ(x0):=∫pθ(x0:N)dx1:N 其中 x 1 , … , x N \mathbf{x}^{1}, \ldots, \mathbf{x}^{N} x1,…,xN 是 D 维的隐变量。
扩散过程:
扩散模型的后验分布 q ( x 1 : N ∣ x 0 ) q\left(\mathbf{x}^{1: N} \mid \mathbf{x}^{0}\right) q(x1:N∣x0)表示为: q ( x 1 : N ∣ x 0 ) = Π n = 1 N q ( x n ∣ x n − 1 ) (1) q\left(\mathbf{x}^{1: N} \mid \mathbf{x}^{0}\right)=\Pi_{n=1}^{N} q\left(\mathbf{x}^{n} \mid \mathbf{x}^{n-1}\right)\tag{1} q(x1:N∣x0)=Πn=1Nq(xn∣xn−1)(1)
扩散模型的后验分布 q ( x 1 : N ∣ x 0 ) q\left(\mathbf{x}^{1: N} \mid \mathbf{x}^{0}\right) q(x1:N∣x0) 是一个不包含训练参数的确定的马尔科夫过程(当前状态只与前一个时刻的状态有关)。扩散模型的扩散过程是一个逐步加高斯噪声的过程:
q ( x n ∣ x n − 1 ) : = N ( x n ; 1 − β n x n − 1 , β n I ) (2) q\left(\mathbf{x}^{n} \mid \mathbf{x}^{n-1}\right):=\mathcal{N}\left(\mathbf{x}^{n} ; \sqrt{1-\beta_{n}} \mathbf{x}^{n-1}, \beta_{n} \mathbf{I}\right)\tag{2} q(xn∣xn−1):=N(xn;1−βnxn−1,βnI)(2)
扩散过程中使用的方差 β 1 , β 2 , . . . , β N ∈ [ 0 , 1 ] \beta_1, \beta_2, ..., \beta_N\in[0,1] β1,β2,...,βN∈[0,1] 是一个单调递增的序列。在此过程中使用重参数化技巧(Re parameter Trick)先从一个标准的高斯分布中采样得到噪声 ϵ \epsilon ϵ 然后将 ϵ \epsilon ϵ 乘以方差 β n I \beta_{n} \mathbf{I} βnI 再加上均值 1 − β n x n − 1 \sqrt{1-\beta_{n}} \mathbf{x}^{n-1} 1−βnxn−1 来获得样本 x n \mathbf{x}^{n} xn。给定输入样本 x 0 \mathbf{x}^0 x0,经 N 步的扩散过程得到加噪后的样本 x N \mathbf{x}^N xN。
扩散过程中要经过多步的加高斯噪声的过程得到最终的 x N \mathbf{x}^N xN, 经过证明,其中每一步加噪后的采样值 x n \mathbf{x}^n xn 可以由 x 0 \mathbf{x}^0 x0 直接计算(将中间的加高斯噪声的步骤合并)如式(3)所示:
q ( x n ∣ x 0 ) = N ( x n ; α ˉ n x 0 , ( 1 − α ˉ n ) I ) (3) q\left(\mathbf{x}^{n} \mid \mathbf{x}^{0}\right)=\mathcal{N}\left(\mathbf{x}^{n} ; \sqrt{\bar{\alpha}_{n}} \mathbf{x}^{0},\left(1-\bar{\alpha}_{n}\right) \mathbf{I}\right)\tag{3} q(xn∣x0)=N(xn;αˉnx0,(1−αˉn)I)(3)
其中, α n : = 1 − β n \alpha_n:= 1-\beta_n αn:=1−βn 且 α ˉ n : = Π i = 1 N α i \bar{\alpha}_n:= \Pi_{i=1}^{N}\alpha_i αˉn:=Πi=1Nαi。
逆扩散过程:
假设逆扩散过程的联合概率分布 p θ ( x 0 : N ) p_{\theta}(\mathbf{x}^{0:N}) pθ(x0:N) 是一个马尔科夫过程, 且每一步的转移概率服从一个带有学习参数的高斯分布(通过神经网络拟合)。此外,逆扩散过程的起始点 p ( x N ) = N ( x N ; 0 , I ) p\left(\mathbf{x}^{N}\right)=\mathcal{N}\left(\mathbf{x}^{N} ; \mathbf{0}, \mathbf{I}\right) p(xN)=N(xN;0,I) 是一个标准的高斯分布(扩散过程不断加噪声,最后得到一个标准的噪声分布),则逆扩散过程的联合分布如式(4)所示:
p θ ( x 0 : N ) : = p ( x N ) Π n = N 1 p θ ( x n − 1 ∣ x n ) (4) p_{\theta}\left(\mathbf{x}^{0: N}\right):=p\left(\mathbf{x}^{N}\right) \Pi_{n=N}^{1} p_{\theta}\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}\right)\tag{4} pθ(x0:N):=p(xN)Πn=N1pθ(xn−1∣xn)(4)
由于扩散过程的每一步都加了很小的高斯噪声,不妨假设每一步的逆扩散过程也服从高斯分布:
p θ ( x n − 1 ∣ x n ) : = N ( x n − 1 ; μ θ ( x n , n ) , Σ θ ( x n , n ) I ) (5) p_{\theta}\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}\right):=\mathcal{N}\left(\mathbf{x}^{n-1} ; \mu_{\theta}\left(\mathbf{x}^{n}, n\right), \Sigma_{\theta}\left(\mathbf{x}^{n}, n\right) \mathbf{I}\right)\tag{5} pθ(xn−1∣xn):=N(xn−1;μθ(xn,n),Σθ(xn,n)I)(5)
其中均值 μ θ ( x n , n ) \mu_{\theta}\left(\mathbf{x}^{n}, n\right) μθ(xn,n) 与方差 Σ θ ( x n , n ) I \Sigma_{\theta}\left(\mathbf{x}^{n}, n\right) \mathbf{I} Σθ(xn,n)I 是输入为当前时刻的 x n \mathbf{x}^{n} xn 与 时刻 n n n 的函数(用神经网络来逼近这个函数,参数为 θ \theta θ), p θ ( x n − 1 ∣ x n ) p_{\theta}\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}\right) pθ(xn−1∣xn) 是为了消除在扩散过程中增加的高斯噪声。
模型训练使得似然函数达到最大,也就是负对数似然函数最小,使用Jensen’s 不等式可以得到负对数似然函数的上界:
min θ E q ( x 0 ) [ − log p θ ( x 0 ) ] ≤ min θ E q ( x 0 : N ) [ − log p θ ( x 0 : N ) + log q ( x 1 : N ∣ x 0 ) ] (6) \min _{\theta} \mathbb{E}_{q\left(\mathbf{x}^{0}\right)}\left[-\log p_{\theta}\left(\mathbf{x}^{0}\right)\right] \leq \min _{\theta} \mathbb{E}_{q\left(\mathbf{x}^{0: N}\right)}\left[-\log p_{\theta}\left(\mathbf{x}^{0: N}\right)+\log q\left(\mathbf{x}^{1: N} \mid \mathbf{x}^{0}\right)\right]\tag{6} θminEq(x0)[−logpθ(x0)]≤θminEq(x0:N)[−logpθ(x0:N)+logq(x1:N∣x0)](6)
等价于优化:
min θ E q ( x 0 : N ) [ − log p ( x N ) − ∑ n = 1 N log p θ ( x n − 1 ∣ x n ) q ( x n ∣ x n − 1 ) ] (7) \min _{\theta} \mathbb{E}_{q\left(\mathbf{x}^{0: N}\right)}\left[-\log p\left(\mathbf{x}^{N}\right)-\sum_{n=1}^{N} \log \frac{p_{\theta}\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}\right)}{q\left(\mathbf{x}^{n} \mid \mathbf{x}^{n-1}\right)}\right]\tag{7} θminEq(x0:N)[−logp(xN)−n=1∑Nlogq(xn∣xn−1)pθ(xn−1∣xn)](7)
由于这些过程都假设为马尔科夫过程,式(7) 可以简化为:
− log p θ ( x 0 ∣ x 1 ) + D K L ( q ( x N ∣ x 0 ) ∥ p ( x N ) ) + ∑ n = 2 N D K L ( q ( x n − 1 ∣ x n , x 0 ) ∥ p θ ( x n − 1 ∣ x n ) ) (8) -\log p_{\theta}\left(\mathbf{x}^{0} \mid \mathbf{x}^{1}\right)+D_{\mathrm{KL}}\left(q\left(\mathbf{x}^{N} \mid \mathbf{x}^{0}\right) \| p\left(\mathbf{x}^{N}\right)\right)+\sum_{n=2}^{N} D_{\mathrm{KL}}\left(q\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}, \mathbf{x}^{0}\right) \| p_{\theta}\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}\right)\right)\tag{8} −logpθ(x0∣x1)+DKL(q(xN∣x0)∥p(xN))+n=2∑NDKL(q(xn−1∣xn,x0)∥pθ(xn−1∣xn))(8)
其中, log p θ ( x 0 ∣ x 1 ) \log p_{\theta}\left(\mathbf{x}^{0} \mid \mathbf{x}^{1}\right) logpθ(x0∣x1) 为逆扩散过程最后一步的条件概率, D K L ( q ( x N ∣ x 0 ) ∥ p ( x N ) ) D_{\mathrm{KL}}\left(q\left(\mathbf{x}^{N} \mid \mathbf{x}^{0}\right) \| p\left(\mathbf{x}^{N}\right)\right) \quad DKL(q(xN∣x0)∥p(xN)) 不包含训练参数,对于模型优化目标而言是个常量,可以省略, D K L ( q ( x n − 1 ∣ x n , x 0 ) ∥ p θ ( x n − 1 ∣ x n ) ) D_{\mathrm{KL}}\left(q\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}, \mathbf{x}^{0}\right) \| p_{\theta}\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}\right)\right) DKL(q(xn−1∣xn,x0)∥pθ(xn−1∣xn)) 为分布 q ( x n − 1 ∣ x n , x 0 ) q\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}, \mathbf{x}^{0}\right) q(xn−1∣xn,x0) 与高斯分布 p θ ( x n − 1 ∣ x n ) p_{\theta}\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}\right) pθ(xn−1∣xn) 之间的KL散度。
对于前向扩散过程中的后验概率 q ( x n − 1 ∣ x n , x 0 ) q\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}, \mathbf{x}^{0}\right) q(xn−1∣xn,x0) 服从高斯分布:
q ( x n − 1 ∣ x n , x 0 ) = N ( x n − 1 ; μ ~ n ( x n , x 0 ) , β ~ n I ) (9) q\left(\mathrm{x}^{n-1} \mid \mathrm{x}^{n}, \mathrm{x}^{0}\right)=\mathcal{N}\left(\mathrm{x}^{n-1} ; \tilde{\mu}_{n}\left(\mathbf{x}^{n}, \mathbf{x}^{0}\right), \tilde{\beta}_{n} \mathbf{I}\right)\tag{9} q(xn−1∣xn,x0)=N(xn−1;μ~n(xn,x0),β~nI)(9)
其中均值与方差:
μ ~ n ( x n , x 0 ) : = α ˉ n − 1 β n 1 − α ˉ n x 0 + α n ( 1 − α ˉ n − 1 ) 1 − α ˉ n x n β ~ n : = 1 − α ˉ n − 1 1 − α ˉ n β n . (10) \begin{array}{c} \tilde{\mu}_{n}\left(\mathbf{x}^{n}, \mathbf{x}^{0}\right):=\frac{\sqrt{\bar{\alpha}_{n-1}} \beta_{n}}{1-\bar{\alpha}_{n}} \mathbf{x}^{0}+\frac{\sqrt{\alpha_{n}}\left(1-\bar{\alpha}_{n-1}\right)}{1-\bar{\alpha}_{n}} \mathbf{x}^{n} \\\\ \tilde{\beta}_{n}:=\frac{1-\bar{\alpha}_{n-1}}{1-\bar{\alpha}_{n}} \beta_{n} . \end{array}\tag{10} μ~n(xn,x0):=1−αˉnαˉn−1βnx0+1−αˉnαn(1−αˉn−1)xnβ~n:=1−αˉn1−αˉn−1βn.(10)
则式(8)中表示两高斯分布的KL散度可以表示为:
D K L ( q ( x n − 1 ∣ x n , x 0 ) ∣ ∣ p θ ( x n − 1 ∣ x n ) ) = E q [ 1 2 Σ θ ∥ μ ~ n ( x n , x 0 ) − μ θ ( x n , n ) ∥ 2 ] + C (11) D_{\mathrm{KL}} \left(q\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}, \mathbf{x}^{0}\right)|| p_{\theta}\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}\right)\right)= \mathbb{E}_{q}\left[\frac{1}{2 \Sigma_{\theta}}\left\|\tilde{\mu}_{n}\left(\mathbf{x}^{n}, \mathbf{x}^{0}\right)-\mu_{\theta}\left(\mathbf{x}^{n}, n\right)\right\|^{2}\right]+C\tag{11} DKL(q(xn−1∣xn,x0)∣∣pθ(xn−1∣xn))=Eq[2Σθ1∥ ∥μ~n(xn,x0)−μθ(xn,n)∥ ∥2]+C(11)
我们的目标是优化模型的权重 θ \theta θ 使得 μ θ ( x n , n ) = μ ~ n ( x n , x 0 ) \mu_{\theta}\left(\mathbf{x}^{n}, n\right) = \tilde{\mu}_{n}\left(\mathbf{x}^{n}, \mathbf{x}^{0}\right) μθ(xn,n)=μ~n(xn,x0),由于直接预测均值得到的效果不好,由公式(3)有 x n ( x 0 , ϵ ) = α ˉ n x 0 + ( 1 − α ˉ n ) ϵ \mathbf{x}^{n}(\mathbf{x}^{0}, \epsilon ) = \sqrt{\bar{\alpha}_{n}} \mathbf{x}^{0} + \sqrt{\left(1-\bar{\alpha}_{n}\right)}\epsilon xn(x0,ϵ)=αˉnx0+(1−αˉn)ϵ, 其中 ϵ ∼ N ( 0 , I ) \epsilon\sim\mathcal{N}(\mathbf{0}, \mathbf{I}) ϵ∼N(0,I),则用 x n \mathbf{x}^{n} xn来表示 x 0 \mathbf{x}^{0} x0有 x 0 = ( x n − β n ϵ / 1 − α ˉ n ) / α n (12) \mathbf{x}^{0} = \left(\mathbf{x}^{n}-\beta_{n} \epsilon / \sqrt{1-\bar{\alpha}_{n}}\right) / \sqrt{\alpha_{n}}\tag{12} x0=(xn−βnϵ/1−αˉn)/αn(12)
我们可以训练模型,使得:
μ θ ( x n , n ) = 1 α n ( x n − β n 1 − α ˉ n ϵ θ ( x n , n ) ) (13) \mu_{\theta}\left(\mathbf{x}^{n}, n\right)=\frac{1}{\sqrt{\alpha_{n}}}\left(\mathbf{x}^{n}-\frac{\beta_{n}}{\sqrt{1-\bar{\alpha}_{n}}} \epsilon_{\theta}\left(\mathbf{x}^{n}, n\right)\right)\tag{13} μθ(xn,n)=αn1(xn−1−αˉnβnϵθ(xn,n))(13)
其中, ϵ θ ( x n , n ) \epsilon_{\theta}\left(\mathbf{x}^{n}, n\right) ϵθ(xn,n) 是一个神经网络,这个网络用来预测 ϵ ∼ N ( 0 , I ) \epsilon\sim\mathcal{N}(\mathbf{0}, \mathbf{I}) ϵ∼N(0,I),最后模型的优化目标可以表示为:
E x 0 , ϵ [ β n 2 2 Σ θ α n ( 1 − α ˉ n ) ∥ ϵ − ϵ θ ( α ˉ n x 0 + 1 − α ˉ n ϵ , n ) ∥ 2 ] (14) \mathbb{E}_{\mathbf{x}^{0}, \epsilon}\left[\frac{\beta_{n}^{2}}{2 \Sigma_{\theta} \alpha_{n}\left(1-\bar{\alpha}_{n}\right)}\left\|\epsilon-\epsilon_{\theta}\left(\sqrt{\bar{\alpha}_{n}} \mathbf{x}^{0}+\sqrt{1-\bar{\alpha}_{n}} \epsilon, n\right)\right\|^{2}\right]\tag{14} Ex0,ϵ[2Σθαn(1−αˉn)βn2∥ ∥ϵ−ϵθ(αˉnx0+1−αˉnϵ,n)∥ ∥2](14)
其中 ϵ \epsilon ϵ 为给定 x 0 \mathbf{x}^0 x0 到 x n \mathbf{x}^n xn 所增加的高斯噪声,并且构建神经网络 ϵ θ ( α ˉ n x 0 + 1 − α ˉ n ϵ , n ) \epsilon_{\theta}\left(\sqrt{\bar{\alpha}_{n}} \mathbf{x}^{0}+\sqrt{1-\bar{\alpha}_{n}} \epsilon, n\right) ϵθ(αˉnx0+1−αˉnϵ,n),使得网络的输出与 ϵ \epsilon ϵ 相等,等价于 μ θ ( x n , n ) = μ ~ n ( x n , x 0 ) \mu_{\theta}\left(\mathbf{x}^{n}, n\right) = \tilde{\mu}_{n}\left(\mathbf{x}^{n}, \mathbf{x}^{0}\right) μθ(xn,n)=μ~n(xn,x0)。有了 μ ~ n ( x n , x 0 ) \tilde{\mu}_{n}\left(\mathbf{x}^{n}, \mathbf{x}^{0}\right) μ~n(xn,x0)便可以由公式(9)得到 q ( x n − 1 ∣ x n , x 0 ) q\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}, \mathbf{x}^{0}\right) q(xn−1∣xn,x0),由于训练过程中,目标是损失最小化,等价于(8)中第三项的两个分布的KL散度为0,也就是 p θ ( x n − 1 ∣ x n ) = q ( x n − 1 ∣ x n , x 0 ) p_{\theta}\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}\right)=q\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}, \mathbf{x}^{0}\right) pθ(xn−1∣xn)=q(xn−1∣xn,x0), 便可以由 x n \mathbf{x}^{n} xn不断计算得到 x n − 1 \mathbf{x}^{n-1} xn−1,最后得到 x 0 \mathbf{x}^{0} x0,也就是训练完成,则有 x n − 1 ∼ p θ ( x n − 1 ∣ x n ) \mathbf{x}^{n-1} \sim p_{\theta}(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}) xn−1∼pθ(xn−1∣xn):
x n − 1 = 1 α n ( x n − β n 1 − α ˉ n ϵ θ ( x n , n ) ) + Σ θ Z (15) \mathbf{x}^{n-1}=\frac{1}{\sqrt{\alpha_{n}}}\left(\mathbf{x}^{n}-\frac{\beta_{n}}{\sqrt{1-\bar{\alpha}_{n}}} \epsilon_{\theta}\left(\mathbf{x}^{n}, n\right)\right)+\sqrt{\Sigma_{\theta}} \mathbf{Z}\tag{15} xn−1=αn1(xn−1−αˉnβnϵθ(xn,n))+ΣθZ(15)
其中 z ∼ N ( 0 , I ) for n = N , … , 2 and z = 0 if n = 1 \mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \text { for } n=N, \ldots, 2 \text { and } \mathbf{z}=\mathbf{0} \text{ if } n=1 z∼N(0,I) for n=N,…,2 and z=0 if n=1
Diffusion Model 的核心思想是使用以 ( x n , n ) (\mathbf{x}^n, n) (xn,n) 为输入的神经网络来逼近后验分布 q ( x n − 1 ∣ x n , x 0 ) q\left(\mathbf{x}^{n-1} \mid \mathbf{x}^{n}, \mathbf{x}^{0}\right) q(xn−1∣xn,x0) , 最后达到使用 x n 与 n \mathbf{x}^n 与 n xn与n 来预测 x n − 1 \mathbf{x}^{n-1} xn−1 的效果。