论文阅读《PatchMatchNet: Learned Multi-View Patchmatch Stereo》

论文地址：PatchmatchNet: Learned Multi-View Patchmatch Stereo
源码地址：https://github.com/FangjinhuaWang/PatchmatchNet

---

一、摘要

  本文提出一个可学习的patchMatchNet，该网络兼顾运算效率与节省运行内存；首次在端到端可训练的体系结构中引入迭代多尺度Patchmatch，并对Patchmatch的核心算法进行了改进，为每次迭代提供了一种新的、经过学习的自适应传播方法；

1. 将Patchmatch思想引入到基于端到端可训练的MVS框架中。此外，将模型嵌入到一个由粗到细的框架中，以加快计算速度。
2. 在Patchmatch传统传播和代价评估步骤上增加了可学习的、自适应的模块，提高了准确度，并且这两个步骤都基于深度特征进行;在源视图的代价聚合期间估计可见性信息。此外，本文提出了一种鲁棒的训练策略，将随机性扰动引入到模型中，提高模型的表达能力；

---

二、网络结构

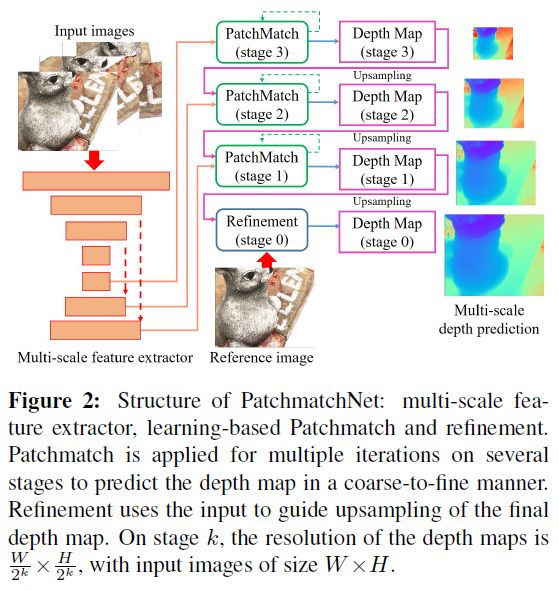
  网络结构主要包含：多尺度特征提取模块、基于学习的patchMatch模块；

2.1 多尺度特征提取模块

  给定 $N$ 张输入图像，其中 $I_0$ 为参考视图，而 $\{I_i{\}}_{i=1}^{N-1}$ 为源视图；使用Feature Pyramid Network（FPN）来提取特征，得到 $k$ 个stage的特征图，特征图大小分别为 $\frac{W}{2^k}\times \frac{H}{2^k}$

2.2 基于学习的PatchMatch

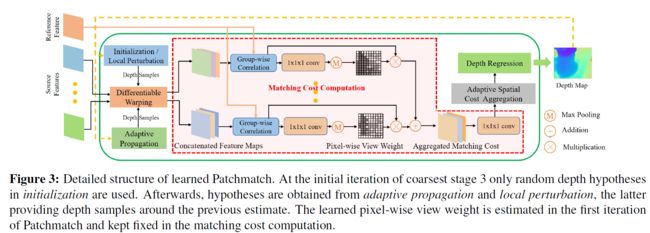
  可学习的PatchMatch包含一下的几个部分：
    1. 初始化：生成随机的假设深度空间或使用上一次迭代得到的深度图的深度上下取两层不同间隔组成深度假设空间；
    2. 传播：在初始化后假设深度空间中增加自适应传播邻域内的点的深度值作为一个像素点的所有深度假设值（增加扰动），得到增加扰动后的深度假设空间；
    3. 评估：通过可微分的单应性变化warp特征、匹配代价计算、自适应空间代价聚合、和深度图回归；
每一个stage的patchMatch模块可以重复迭代多次得到更优的深度图；

2.2.1 初始化与位置随机扰动

  在首次初始化时，在预设的 $[d_{min},d_{max}]$ 的范围内，对于每个像素在深度范围内采样得到深度的倒数(深度与视差成反比，因此此步可以视为在视差空间中进行采样)，这操作助于模型适用于复杂和大规模的场景；
  在第一次初始化时候，使用平行窗口的方式来初始化代价体，得到初始深度图，在初始深度图的基础上增加随机扰动，在像素平面取邻域点的深度值和该点的深度维度上下采样深度值，在这些深度值中找代价最小的深度值作为当前点的深度值。

2.2.2 自适应深度传播

  一般情况下，深度值的空间一致性只存在于同一个物理表面上，为此本文不像吉布斯采样和DeepPruner一样在静态邻域中进行传播，而自适应在同一个平面上进行深度传播，这样的操作有利于PatchMatch 快速收敛且得到更好精度的深度图，如下图所示：
  这种自适应传播策略倾向于从同一表面的像素为纹理对象或无纹理区域收集假设，使我们能够有效收集更多有效的深度假设值；在实际操作中，我们使用可变形卷积来实现自适应传播，对于 stage $K_p$ 中的像素点 $p$ ，模型先学习一个 2D 偏置 ${\left\{\Delta {\mathbf{O}}_i(\mathbf{p})\right\}}_{i=1}^{K_p}$ 应用在一个固定的2D偏置${\left\{{\mathbf{O}}_i\right\}}_{i=1}^{K_p}$ 上。我们使用一个2D CNN来对特征图 $F_0$ 进行推理得到对于每个像素 $p$ 的2D 偏置，然后使用双线性插值得到深度假设空间 $D_p(\mathbf{p})$如式1所示：
$${\mathbf{D}}_p(\mathbf{p})={\left\{\mathbf{D}\left(\mathbf{p}+{\mathbf{o}}_i+\Delta {\mathbf{o}}_i(\mathbf{p})\right)\right\}}_{i=1}^{K_p}\text{\hspace{1em}(1)}$$
其中 $\mathbf{D}$ 为上一个迭代轮次得到的深度图经过上采样得到的深度图；

2.2.3 自适应评估

自适应评估包含以下几个步骤：可微分的单应性变化、匹配代价计算、自适应空间代价聚合、和深度图回归；
可微分单应性变化：在已知每个视图的相机内参 ${\left\{K_i\right\}}_{i=0}^K$ 与参考视图与源视图的变换矩阵 ${\left\{\left[{\mathbf{R}}_{0,i}\mid {\mathbf{t}}_{0,i}\right]\right\}}_{i=1}^K$ 的前提下，由预测的初始深度图 $D$ ，可以求出参考视图点 $p$ 在源视图上的对应像素点 $p_{i,j}$的位置，两者的关系如式2所示：
$${\mathbf{p}}_{i,j}={\mathbf{K}}_i\cdot \left({\mathbf{R}}_{0,i}\cdot \left({\mathbf{K}}_0^{-1}\cdot \mathbf{p}\cdot d_j\right)+{\mathbf{t}}_{0,i}\right)\text{\hspace{1em}(2)}$$
通过这个关系，可以将源视图上的信息warp到参考视图中，过程中需要通过双线性插值得源视图上到亚像素的信息${\mathbf{F}}_i\left({\mathbf{p}}_{i,j}\right)$；

匹配代价计算：文中在代价聚合过程中使用可见性图（全局注意力图）增加鲁棒性。其中${\mathbf{F}}_0(\mathbf{p}),{\mathbf{F}}_i\left({\mathbf{p}}_{i,j}\right)\in {\mathbb{R}}^C$表示参考视图与源视图中对应像素的特征向量，将特征向量分为 $G$ 组，${\mathbf{F}}_0(\mathbf{p}{)}^g,{\mathbf{F}}_i{\left({\mathbf{p}}_{i,j}\right)}^g$ 和第g组的相似性 ${\mathbf{S}}_i(\mathbf{p},j{)}^g\in \mathbb{R}$ 计算方式如式3所示：
$${\mathbf{S}}_i(\mathbf{p},j{)}^g=\frac{G}{C}⟨{\mathbf{F}}_0(\mathbf{p}{)}^g,{\mathbf{F}}_i{\left({\mathbf{p}}_{i,j}\right)}^g⟩\text{\hspace{1em}(3)}$$
其中$<.，.>$ ；${\mathbf{S}}_i(\mathbf{p},j)\in {\mathbb{R}}^G$为每组向量的相似性；$S_i\in {\mathbb{R}}^{W\times H\times D\times G}$，pathchMatchNet计算两个视图之间的匹配代价方式与MVSNet是不同，本文是用warp到参考视图的特征向量与参考视图的特征的分组后的内积来计算匹配代价（对应位置的特征向量越不相同，代价越大）
  为了得到像素级别的权重 ${\left\{{\mathbf{w}}_i(\mathbf{p})\right\}}_{i=1}^{N-1}$，在第一次迭代得到初始深度假设空间的基础上，使用 $w_i(p)$来表示源视图 $I_i$ 中的像素 $p$ 可视程度，这个权重只计算一次，并且后面的迭代过程中都使用这个权重；
  使用一个 包含 $1\times 1\times 1$卷积核的与sigmoid激活层的3D 卷积来对相似度矩阵 $S_i$ 处理得到一个介于 0~1 之间的概率体 $P_i\in {\mathbb{R}}^{W\times H\times D}$，对于 $I_i$ 视图的 $p$ 点，其权重值表示如式4所示：
$${\mathbf{w}}_i(\mathbf{p})=\max \left\{{\mathbf{P}}_i(\mathbf{p},j)\mid j=0,1,\dots ,D-1\right\}\text{\hspace{1em}(4)}$$
其中 $P_i(p,j)$ 表示在点 $p$ 在深度为 $j$ 层时的可视概率，可以将这里的权重图 $w_i$ 视为第 $i$ 个视图相对于参考视图的全局注意力权重图；
  有了每个视图的像素可视图$w_i$（全局注意力权重图）与匹配代价图 $S_i$，用权重图对代价体进行加权，对于所有源视图，对于第 $j$ 深度层的像素点 $p$ ，其组相似性表达式如式 5 所示：
$$\overline{\mathbf{S}}(\mathbf{p},j)=\frac{{\sum }_{i=1}^{N-1}{\mathbf{w}}_i(\mathbf{p})\cdot {\mathbf{S}}_i(\mathbf{p},j)}{{\sum }_{i=1}^{N-1}{\mathbf{w}}_i(\mathbf{p})}\text{\hspace{1em}(5)}$$
其中：$i$ 表示第 $i$ 个源视图， $\overline{\mathbf{S}}\in {\mathbb{R}}^{W\times H\times D\times G}$，最后使用一个 3D 卷积和 1x1x1的卷积核来得到单个代价$\mathbf{C}\in {\mathbb{R}}^{W\times H\times D}$，这个代价值表示某个像素在所有深度层的匹配代价值；
自适应空间代价聚合：
  为了防止邻域中属于不同平面上的像素进行聚合，提出了一种基于PatchMatch与AANet的自适应空间聚合策略，对于空间窗口 $K_e$ 的像素 $\{p_k{\}}_{k=1}^{K_e}$ ,将其组织为一个网格，对于每个像素都学习一个偏置 ${\left\{\Delta {\mathbf{p}}_k\right\}}_{k=1}^{K_e}$ ，空间聚合代价 $\tilde{\mathbf{C}}(\mathbf{p},j)$ 定义如式 6 所示：

$$\tilde{\mathbf{C}}(\mathbf{p},j)=\frac{1}{{\sum }_{k=1}^{K_e}{w}_k{d}_k}\sum _{k=1}^{K_e}{w}_k{d}_k\mathbf{C}\left(\mathbf{p}+{\mathbf{p}}_k+\Delta {\mathbf{p}}_k,j\right)\text{\hspace{1em}(6)}$$

其中： $w_k$是基于中心像素与自适应聚合邻域像素的相似性来计算权重 ； $d_k$ 基于中心像素的深度与自适应聚合邻域内邻域像素的深度相似度对来计算，通过这两个自适应权重来对代价 $C$ 进行加权；与自适应传播类似，先对每个中心点的像素加上一个标准的邻域偏置 $p_k$ 得到标准邻域的坐标，再加上一个学习到的自适应偏置位置量$\Delta {\mathbf{p}}_k$，每个像素的偏置量${\left\{\Delta {\mathbf{p}}_k\right\}}_{k=1}^{K_e}$ 由一个2D CNN 来对 特征图 $F_0$ 操作而得到；

  聚合邻域点的采样位置保持在对象边界内，而对于无纹理区域，采样点聚集在更大的空间环境中，这可能会降低估计的不确定性。

深度图回归：
  使用softmax来对代价体$\tilde{\mathbf{C}}$ 的深度维度处理得到概率体 $P$ ，最基于期望的形式对概率体进行回归得到深度图如式7所示：
$$\mathbf{D}(\mathbf{p})=\sum _{j=0}^{D-1}{d}_j\cdot \mathbf{P}(\mathbf{p},j)\text{\hspace{1em}(7)}$$

深度图优化：
  核心思想与MVSNet一致，使用RGB图来引导深度图优化，此步操作基于MSG-Net，设计了深度残差网络来对视差图进行优化；为了避免深度范围对网络性能的影响，将输入深度图缩放为范围[0;1]进行处理，并在处理后还原为原来的深度范围；该网络学习输出一个残差，将其加入到Patchmatch输出的 $D$ 的(上采样）深度图上，以得到改进的深度图 $D_{ref}$，该网络独立地从 $D$ 和 $I_0$ 提取特征 $F_D$ 和$F_I$ ，并对 $F_D$ 进行反卷积，将特征映射上采样到图像大小，在特征图、深度图和图像的拼接上应用多个二维卷积层来传递深度残差。

---

损失函数

损失函数 $L_{total}$ 考虑了所有深度估计中的损失:
$$L_{\text{total }}=\sum _{k=1}^3\sum _{i=1}^{n_k}{L}_i^k+L_{\text{ref }}^0\text{\hspace{1em}(8)}$$

其中，计算了所有 $L_i^k$ 与Ground True 的 $L_1$ 损失，$i$ 表示第 $i$ 个视图, $k$ 表示第 $k$ 个stage，$L_{\text{ref }}^0$ 表示细化后深度图的损失；

---

实验结果