Big Bird: Transformers for Longer Sequences(2020-7-28)
模型介绍
基于Transformers 的模型,例如BERT,在各种自然语言处理(NLP)任务中都取得了巨大的成功,因此成为现代NLP研究的主体。它们的多功能性和鲁棒性是被广泛的主要原因。transformer的关键创新是引入了一种self-attention机制,该机制可以针对输入序列的每个token进行并行评估,从而消除了循环神经网络(如LSTM)中的顺序依赖性。这种并行性使Transformers能够充分利用现代SIMD硬件加速器(如GPU/TPU)的全部功能,从而有助于在规模空前的数据集上训练NLP模型。
self-attention机制通过允许输入序列中的每个token,独立地注意序列中的其他每个token,从而克服了RNN的约束(即RNN的顺序性质)。 这种设计选择具有几个有趣的影响。 尤其是,完全的self-attention对计算和内存的要求是序列长度的平方。 我们注意到,尽管语料库可以很大,但在许多应用程序中提供上下文的序列长度却非常有限。 使用当前可用的常用硬件和模型大小,要求可以转换为大致能够处理长度为512个token的输入序列。 这降低了其直接适用于需要较大上下文的任务,例如QA ,文档分类等。
BIGBIRD从图分散方法中汲取了灵感,从全注意力生成到提议的注意力。BIGBIRD包括三个主要部分:
- 一组g个全局token,它们参与序列的所有部分。(全局注意力)
- 对于每个query qi,每个query将关注r个随机key的集合。 (随机注意力)
- 一个局部邻居块w,以便每个节点关注其局部结构。 (对应窗口滑动注意力)
模型结构
使用广义注意力机制描述BIGBIRD模型,该机制用于在输入序列 X = ( x 1 , . . . , x n ) ∈ R n × d X=(x_1,...,x_n) \in R^{n×d} X=(x1,...,xn)∈Rn×d上的Transformer运行的每一层。广义注意力机制由顶点集 [ n ] = { 1 , . . . , n } [n]=\{1,...,n\} [n]={1,...,n}组成的图 D D D 所描述。弧(有向边)集表示注意力机制将考虑的内积。 令 N ( i ) N(i) N(i) 表示 D D D 中节点 i i i 的邻居集,则广义注意力机制的第 i i i 个输出向量定义为:
A T T N D ( X ) i = x i + ∑ h = 1 H σ ( Q h ( x i ) K h ( X N ( i ) ) T ) ⋅ V h ( X N ( i ) ) ATTN_D(X)_i=x_i+\displaystyle\sum^H_{h=1} \sigma(Q_h(x_i)K_h(X_{N(i)})^T)\cdot V_h(X_{N(i)}) ATTND(X)i=xi+h=1∑Hσ(Qh(xi)Kh(XN(i))T)⋅Vh(XN(i))
这里 Q h , K h : R d → R m Q_h,K_h:R^d \rightarrow R^m Qh,Kh:Rd→Rm 分别是query函数和key函数, V h : R d → R d V_h:R^d \rightarrow R^d Vh:Rd→Rd 是value函数, σ \sigma σ 是得分函数(softmax或者hardmax), H H H 表示头数。还要注意 X N ( i ) XN(i) XN(i) 对应于仅堆叠 { x j : j ∈ N ( i ) } \{x_j:j \in N(i) \} {xj:j∈N(i)} 而不是所有输入组成的矩阵。
如果D是完整的有向图,我们将恢复完全的平方注意力机制;如果基础图是稀疏的,我们将对图D的邻接矩阵A进行操作。详细地说,如果query i和 key j有关联,那么 A ( i , j ) = 1 , A ∈ [ 0 , 1 ] n × n A(i,j)=1,A \in [0,1]^{n×n} A(i,j)=1,A∈[0,1]n×n;否则(query i和 key j没有关联),那么 A ( i , j ) = 0 A(i,j)=0 A(i,j)=0。
模型改进
将self-attention视为全连接的图的观点,使我们能够利用现有的图论来帮助降低其复杂性。降低self-attention的平方复杂性的问题,现在可以看作是图分散化问题。
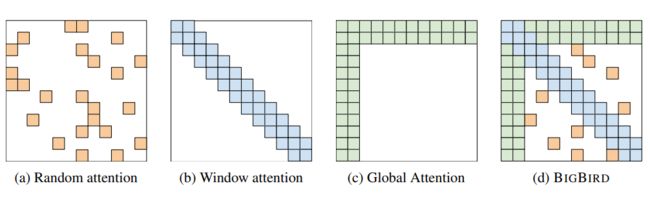
随机注意力
考虑最简单的随机图构造,每个边以固定概率独立选择。 在这样的具有约 O ( n ) O(n) O(n) 个边的随机图中,任意两个节点之间的最短路径的节点数是对数的。结果,这样的随机图在频谱上近似了整个图,并且它的第二个特征值(邻接矩阵的)与第一个特征值相距很远。 此属性会导致在grpah中随机游走的快速混合时间,这非形式上表明,信息可以在任何一对节点之间快速流动。
因此,提出一个稀疏的注意力,其中每个query都关注r个随机数的key,即对于r个随机选择的key, A ( i , ⋅ ) = 1 A(i,\cdot)=1 A(i,⋅)=1。
滑动窗口注意力
NLP的大多数上下文都具有显示大量参考位置的数据。在这种现象中,可以从邻近的token中获得大量有关token的信息。在BIGBIRD中,定义了滑动窗口注意力,以便在宽度 w 的 self-attention 期间,位置 i 的 query 关联从 i-w/2 到 i+w/2 的key,用符号表示为 A ( i − w / 2 , i + w / 2 ) = 1 A(i-w/2,i+w/2)=1 A(i−w/2,i+w/2)=1。
全局注意力
利用了“全局token”的重要性(全局token属于序列中的所有token,所有token都关注它们)。这些全局token可以通过两种方式定义:
BIGBIRD-ITC:在内部transformer构造(ITC)中,我们将一些现有token“全局”化,并在整个序列中使用。 具体来说,我们选择索引的子集G(具有 g : = ∣ G ∣ g:=|G| g:=∣G∣),对于所有 i ∈ G , A ( i , : ) = 1 , A ( : , i ) = 1 i \in G,A(i,:)=1,A(:,i)=1 i∈G,A(i,:)=1,A(:,i)=1。
BIGBIRD-ETC:在扩展transformer(ETC)构造中,我们包括其他“全局”token,例如CLS。 具体来说,我们添加g个全局token,这些全局token关注所有现有token。 用我们的符号表示,这相当于通过向矩阵A添加g行来创建一个新的矩阵 B ∈ [ 0 , 1 ] ( N + g ) × ( N + g ) B \in [0,1]^{(N+g)×(N+g)} B∈[0,1](N+g)×(N+g)。这样对于所有 i ∈ { 1 , 2 , . . . , g } , B ( i , : ) = 1 , B ( : , i ) = 1 i \in \{1,2,...,g\},B(i,:)=1,B(:,i)=1 i∈{1,2,...,g},B(i,:)=1,B(:,i)=1和对于所有 i , j ∈ { 1 , 2 , . . . , N } , B ( g + i , g + i ) = A ( i , j ) i,j \in \{1,2,...,N\},B(g+i,g+i)=A(i,j) i,j∈{1,2,...,N},B(g+i,g+i)=A(i,j)。这将增加额外的位置来存储上下文,并且正如我们将在实验中看到的那样,可以提高性能。
组合注意力
BIGBIRD的最终注意力机制具有以下所有三个属性:
1、query关注r个随机key
2、每个query关注其位置左侧的w/2个token
3、其位置右侧的w/2和它们包含g个全局token(全局token可以来自现有token或额外添加的token)。
模型参考
论文地址:https://arxiv.org/abs/2007.14062
代码地址:https://github.com/google-research/bigbird