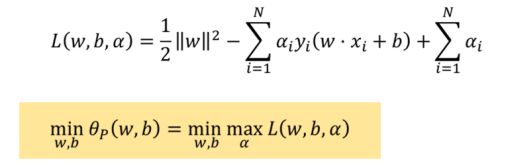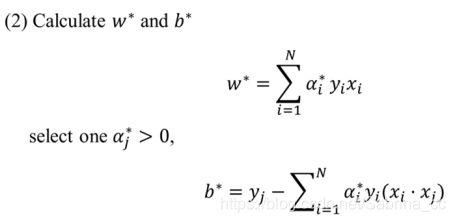机器学习-支持向量机 -- 硬间隔SVM
一、概述
1. 支持向量机(Support vector machine, SVM)解释
2. SVM三宝
3. SVM的三个重要的算法
二、硬间隔SVM(Linearly separable patterns -- Hard-margin SVM)
1. 预知识
2. Hard-margin SVM
3. 函数间隔 VS 几何间隔
4. 最大间隔化
5. 硬间隔SVM的算法描述
6. 支持向量
7. 硬间隔SVM例题
8. 对偶问题
9. 线性支持向量机的算法(根据对偶问题得到的)
10. 使用对偶解题例题
支持向量机(Support vector machine)
一、概述
SVM是一种小样本学习方法。
少数支持向量决定了最终结果,对异常值不敏感, 这不但可以帮助我们抓住关键样本、“剔除”大量冗余样本,而且注定了该方法不但算法简单,而且具有较好的“鲁棒性”
SVM学习问题可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值
有优秀的泛化能力。
1. 支持向量机(Support vector machine, SVM)解释:
(1)支持向量(support vector):支持或支撑平面上把两类类别划分开来的超平面的向量点。
(2)“机”(机器,machine):“机”实质上是一个算法。在机器学习领域,常把一些算法看做是一个机器,如分类机(当然,也叫做分类器),而支持向量机本身便是一种监督式学习的方法,它广泛的应用于统计分类以及回归分析中。
2. SVM三宝:
(1)间隔(margin):用于建模
(2)对偶(duality):用于模型求解
(3)核技巧(kernel trick):将非线性问题转化为线性问题
3. SVM的三个重要的算法:
(1)Hard-margin SVM 线性可分的SVM
(2)Soft-margin SVM 线性不可分的SVM
(3)Kernel SVM (Nonlinear SVM) 非线性
二、硬间隔SVM(Linearly separable patterns -- Hard-margin SVM)
1. 预知识:
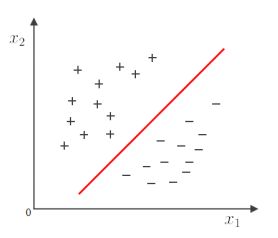
线性模型:在样本空间中寻找一个超平面, 将不同类别的样本分开.
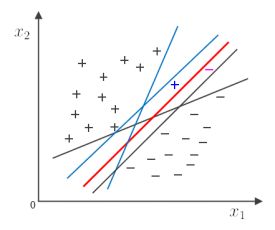
-Q:将训练样本分开的超平面可能有很多, 哪一个好呢?
-A:应选择”正中间”, 容忍性好, 鲁棒性高, 泛化能力最强.
2. Hard-margin SVM
输入空间:欧几里德空间或离散集(Euclidean space or discrete set)
输出空间:欧几里得空间或希尔伯特空间(Euclidean space or Hilbert space)内积空间
假设:输入空间的实例可以映射到特征空间中的特征向量。(一对一)。学习是在特征空间中进行的
训练数据集:
目标:找到一个超平面 wx + b = 0 (w,b为参数)
思路:间隔最大(maximum margin)
线性支持向量机SVM:
3. 函数间隔 VS 几何间隔
确信度(confidence):|w x + b|
正确性(correctness):w x + b与y符号相同时,表示预测正确,相反w x + b与y符号相反时,表示预测错误,则正确的可以写成 y ( w x + b )
因此结合确信度和正确性 可以得到:y ( w x + b )
(1)函数间隔
给定训练数据集T,平面(w,b)
目前可以得到这样的结果。
但是,如果将w变为2w,b变成2b,超平面不会发生变化,但是函数间隔变化了
因此:我们选择使用||w|| ( w的二范数)
从而引出几何间隔
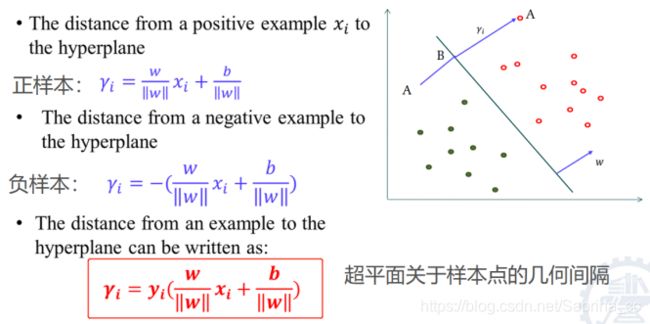
(2)几何间隔
4. 最大间隔化
基本思想:求解能正确划分训练数据集,且geometric margin 最大的分离超平面(唯一)
间隔最大化又称硬间隔最大化(Maximum Hard-margin)
直观解释:对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据进行分类。也即,不仅将正负实例点分开,而且对最难分的实例点(离超平面最近的点)也有足够大的确信度将它们分开。这样的超平面应对未知的新实例有很好的分类预测能力。
如何求该超平面?几何间隔最大化(最优化)
(每个样本的几何间隔至少是r)
我们令 r=1
(实质是一个凸二次规划)
5. 硬间隔SVM的算法描述
输入:训练集T
输出:最大间隔超平面w* x + b
得到最大间隔超平面和决策函数
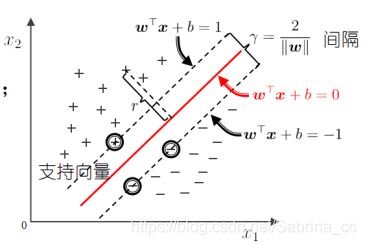
6. 支持向量
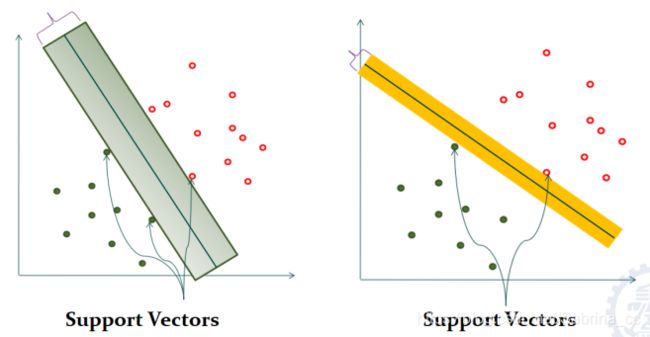
支持向量:离超平面最近的点,即满足不等式取等的时候
长带的宽度:H1和H2的距离叫间隔margin
H1和H2称作间隔的边界
H1和H2上的训练样本点叫支持向量
中间线上的叫支持向量机
在决定分离超平面时只有支持向量起作用;其他的点不影响求解
若移动支持向量将改变所求的解;但若在间隔边界以外移动其他实例点,甚至去掉这些点,则解释不好改变的。
由于支持向量在确定分离超平面中起决定性作用,故这种分类模型称支持向量机。
支持向量的个数一般很少,所有支持向量机由很少的“重要的”训练样本确定。
7. 硬间隔SVM例题
由于当训练集比较大时,手动解法很复杂,因此我们引入对偶问题
8. 对偶问题
原始问题--->对偶问题
目的:方便解决问题和方便引入核函数(非线性分类变为线性分类)
如何进行对偶理论不再此讲解
原始问题:
对于每一个约束,引入一个拉格朗日参数a,因此问题转化为:
对于求解对偶问题,我们调换min和max,因此得到了原始问题的对偶问题:
求解对偶问题
求解对偶问题,就是要解w,b,a
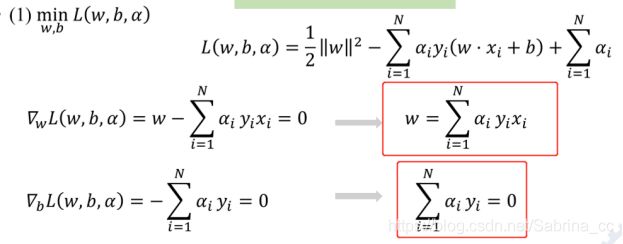
先求拉格朗日函数的最小问题----求导
求出对w和b的导数之后,可以解出w以及关系
将求出来的两项带入拉格朗日函数中,
因此问题进一步得到转化
(2)接下来求a,求最大
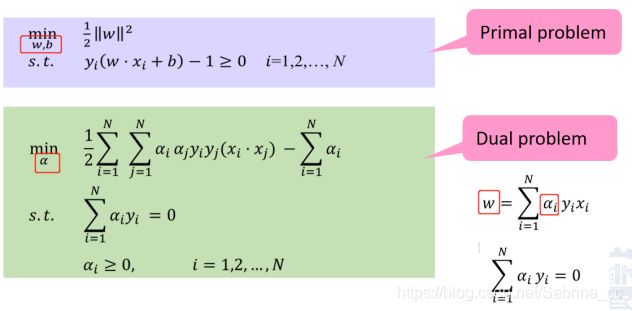
由于max中有一个负号,我们将其取出,就变成了min最小化问题,如下
至此我们就完成了原问题到对偶问题的转化
可以看出,原问题是对w,b求解,对偶问题是对a求解,求出a就可以算出w,但是b怎末求呢?给出如下定理,可以直接使用:
并且w* 和b*都是唯一的
因此,求出了w*和b*就可以求出分离超平面和决策函数
此处可以看出,超平面和决策函数都是由内积决定的(后面会讲)
9. 线性支持向量机的算法(根据对偶问题得到的)
输入:训练集T
输出:最大间隔超平面和决策函数
(1)构造并求约束问题的对偶问题,从而求出a*
(2)由a*可以求出w*和b*
(3)从而得到最大间隔超平面和决策函数
因此可以对未知样例进行预测(带入式子计算出正类或负类)
总结:求间隔最大化的原始问题,通过对偶理论得到对偶问题,利用对偶问题可以求a*,有了a*可以求w*和b*,从而得到最大间隔超平面(也就是分类器)以及决策函数。
10. 使用对偶解题例子
题目的考法:
- 求支持向量
- 求最大间隔超平面
- 决策函数
- 预测样本
总结:本节讲述了线性可分的SVM,是比较特殊的SVM,在实际中可能会由奇异点等,是非线性问题,因此需要情况的转化,下节会继续说明。