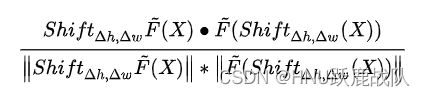了解CV和RoboMaster视觉组(五)CNN没有不变性?
[email protected]
5.5.3.4. ConvNet没有不变性!?
我们已经阐述过使用不变特征的好处,那么AlexNet在ImageNet竞赛上大杀四方的时候,是否就意味着DCNN已经拥有了我们所需要的一切invariant feature?让我们一一揭晓:
5.5.3.4.1. 旋转不变性
从直观上来说,CNN不具有旋转不变性,这是一个显而易见的结论,物体在旋转之后通过卷积核显然会得到不同的响应;之后更深层的卷积也会受到第一层输出的影响,因此最后生成的特征(比如softmax之前的一层,我们可以把最后一层的Fully connect+softmax当作分类器,前层都当作feature extractor)显然和旋转前不同。那么为什么我们的分类器和检测器仍然可以正确地完成分类、进行识别呢?这是因为我们的训练集中含有旋转过的数字,或我们使用了数据增强中的旋转操作。在《深度学习》(花书)中给出了一个数字识别的例子:
中间的一排表示用于匹配不同模式的filter
对于每一层的卷积操作,我们一般都拥有多组卷积核,而对于经过不同角度旋转的输入,对应不同通道的卷积核就能学习到这种旋转。如左上所示,左侧的卷积核对于向右倾斜45°的数字9会产生较大的响应,中间的则是对稍微向左侧倾斜的9有较大的响应;因此,在之后的最大池化操作中,这些响应都会被归结为”这里有一个9“而输出。那么这些不同的filter为什么会对不同的9有响应呢?那不就是训练出来的吗:我们的数据集中有不同转角的数字9,经过数轮反向传播之后不同通道不同组的卷积核自然而然就学习了某一种旋转模式。
当然,”旋转不变性“也不一定是从卷积层学到的,很可能是在全连接阶段,拥有不同转角的输入在经过非线性映射后投影到了特征空间中相近的位置也是一种可能的解释。最有力的证明就是进行实验,对每一层的feature map进行可视化,画出heat map。感兴趣的同学可以阅读本章末的paper。
但是不管怎么说,神经网络最后的输出应该是相近的,只是在单个卷积核提取特征的时候,由于使用的是卷积操作因此并不具有roration invariant特性;那数据增强和filter组合技算不算赋予了CNN以旋转不变性呢?这就是一个智者见智仁者见仁的问题了。
虽然一般我们没有显式地对物体的旋转进行建模,但是数据增强的确让网络在最后学习到了旋转不变性(data aug和filter group的组合),倘若我们为网络增加一些先验知识,并且直接建模旋转这一变量,网络是否更容易应对旋转的情况?这就是Spatial Transformer。这里的transformer不是自注意力的那个,代表的是变换的“那个” transform。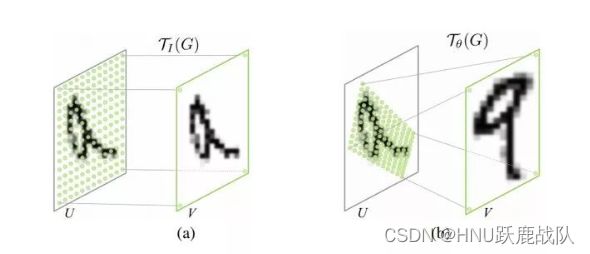
左侧为一般卷积,右侧为加入了ST模块之后的输出
Spatial Transformer会通过反向传播学习一组仿射变换的参数(平移+旋转)用于将图像中关键的部分“摆正”,在变换的过程中可能会出现拉伸或压缩,原文选择了双线性插值的方法。同时ST还可以切除没有用的背景信息,这又有一点注意力机制的意味(实际上也确实是一种隐式的注意力)。不过,我们还是需要不同转角的输入以训练ST module,否则单单输入垂直的目标,网络仍然无法学会这种变换。
此外,在 5.2.5.2 介绍池化层的时候,提到了pooling会使得当前层提取的特征拥有一定的旋转不变性和平移不变性,能够应对轻微的变化。然而有时候pooling反而会破坏这种不变性,我们稍后会介绍其中的缘由。
5.5.3.4.2. 尺度不变性
和旋转不变性一样,神经网络不具备尺度不变性的原因相同,除非使用数据增强。从最早的spatial pyramid pooling到最新的PAN,我们可以FPN的发展轨迹略知一二:如果CNN拥有scale invariant特征,为什么还要费尽心思地进行多尺度特征融合?
对不同尺度特征的感受能力还和卷积核的感受野有关,扩大感受野也是膨胀卷积(dilate conv,atrous conv)提出的目的。YOLOF(you only look one-level feature)就另辟蹊径,主张利用不同stride的膨胀卷积提取不同尺度的特征并进行融合,从而抛弃了FPN的设计。不过当下大热的Vision Transformer通常也不需要利用FPN建模不同尺度的特征,似乎自注意力能够自动聚焦到不同大小的目标和特征上,因此也引领了研究的新潮流。
YOLOF在四个res block里的3x3卷积采用了不同dilate rate的空洞卷积
5.5.3.4.4. 光照、对比度、颜色不变性
如果有,为什么还要用数据增强?但是,输入归一化(这也算是现代神经网络的标配了)和BN从原理上来说,似乎可以给CNN提供这些不变性。笔者猜测,之所以继续使用光照、对比度、颜色变化的数据增强,是因为这些变量常常是协变的,单单用BN很难解决这种像素级的耦合变化。
5.5.3.4.3. 平移不变性
CNN是否具有平移不变性是这几个问题中最具有争议性的一个。数篇论文尝试通过理论分析、实验的方法解释这个问题,却得到迥异的结果,大家的争论主要集中在以下两点:
-
CNN中的平移不变性到底代表什么?
-
CNN是否具有上述的”那种平移不变性”?
移动轻微移动图像后,classifier输出的置信度变化剧烈
图源https://zhuanlan.zhihu.com/p/77543304
-
纯卷积拥有“平移同变性”
卷积作为线性算子,对于图像这个线性输入进行操作显然具有“空间不变”性质(对应于LTI的时不变性质),因此,对于平移后的图像进行卷积,产生的响应只会在空间上平移对应的间隔。因此,若CNN全部由卷积构成而不加入pooling和fc,那么图像发生平移,最后输出的feature map也会平移相应的距离,但是响应大小仍然不变。
我们称这种性质为平移同变性,即输入图像的平移只改变响应的位置而不改变大小,但是显然输出特征是和原来不同的,两者相差一个位移。故不是”平移不变性“而是同变性。 那么拥有特征拥有平移同变性有什么好处?那就是更容易被分类器划分(虽然不如平移不变性那么容易,因为还需要平移一个距离,即增加bias)。
另外,前面在介绍旋转不变性的时候我们提到,pooling可以选择响应最大的特征。如果一组filter对应某个特征(当它遇到特定的边缘区域、角落或颜色斑点时将拥有很大的响应),那不管是该组的哪一个滤波器有激活,我们都可以检测到这个特征的出现(presence),一旦数个特征的组合出现并且有较大的响应值,我们就任务图像中存在这些特征的组合所对应的物体。若这种猜想成立,也同样佐证了平移同变性的重要性,并且说明严格的平移不变性并不是那么重要的。
显然,平移同变性只是让网络有能力学习到不同位置的物体特征,我们同样需要使用数据增强的方法让特征出现在feature map的每一个位置。
-
pooling是同变性消失的罪魁祸首
pooling确实可以提供一定的平移不变性(注意和同变性的差别),但是处在边界的时候,pooling的境地就很尴尬了:
上方为原始”图像”,下方为左移一个单位后的图像;图源https://zhuanlan.zhihu.com/p/77543304
不失一般性,我们使用一维的信号举例。上图中的shift0代表原图,其pooling步长为2,输出为0101;shift1则是信号左移一个单位,但是由于原本的响应恰好处于边缘处,导致输出变成了1111,完全丢失了平移不变性和同变性!当且仅当移动的距离等于pooling的采样步长时,平移同变性可以保持(相同的像素移动到了下一个pooling窗口,因此响应的位置改变但是值不改变)。可是上面不是提到只要特征出现分类器就能正确分类 吗?那么pooling之后特征只是在位置上发生了偏移,并不影响我检测这个物体啊?还是拿上图的例子说明,假设网络认为0101代表一种特征组合的模式,即某种物体具有这样的特征组合,那经过shift后组合就变为了1111,很可能就是另一种模式了。不过好在神经网络的参数量较大,同时拥有多个通道用于组合不同的模式,有较强的抗噪能力,即使在一处发生了错位,也不会影响最终的结果(不过其实从本节开始处的动图来看,平移的影响还是比较大的)。
除了pooling,strid而不等于1的卷积同样会丢失特征的平移同变性,除非位移值和stride相同,原因和pooling相同;更不用说dilate conv、deformable conv这些不规则卷积了。
上面的解释都是定性的,若要从定量角度分析,则需要一个同变性丢失程度的度量:shiftability。在Making Convolutional Networks Shift-Invariant Again这篇论文中,作者采用余弦相似度来衡量平移不等的程度:
上式中的\tilde F(X)即卷积操作,Shift_{\Delta h,\Delta w}则表示height和width方向上的移位。其实就是对比先移位后卷积和相反操作得到的feature map的相似性。既然有了度量方法,就该思考如何减小pooling带来的影响,请看下面。
-
抗锯齿:anti-aliasing
喜欢玩游戏的同学可能在游戏设置中看到过这个调节选项,学习过数字图像处理/计算机图形学的同学多少都了解这个概念和采样定律的关系。这篇文章的思路非常有趣,从传统信号处理的角度入手解决pooling带来的问题。它将pooling视作下采样操作,根据Nyquist’s law,倘若采样得到的信号要保有原信号的所有信息,采样频率至少为原信号最高频的两倍。空间域的卷积等价于频域的乘法,这也是采样定律应用的核心。但max pooling显然不是卷积操作也不是线性算子,无法在频域被解析描述(或者说没有频谱/频谱没有函数式),故丢失了前述的平移同变性。
pooling的size和stride相同,也可以看作是一种欠采样的操作。欠采样会带来频谱混叠的问题,再次回到本节初的那张识别小鸟的动图我们会发现,置信度周期性地变大-变小,而离散频谱正是周期性的!
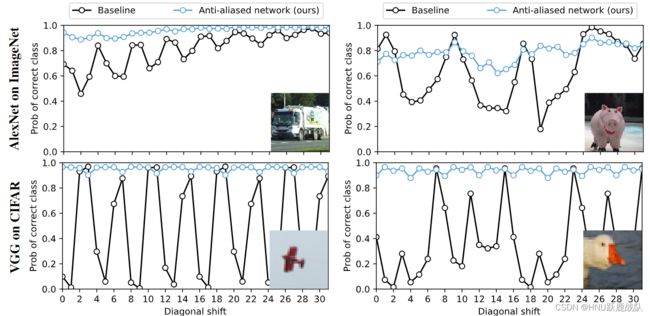
不同图像在对角线上移动的时候置信度的变化
经典的解决频谱混叠的方法就是加入抗混叠滤波器(低通滤波器),average pooling其实就引入了一定的模糊效果(均值滤波器的频率响应是一个低频处增益接近1,高频增益呈小幅度波浪状的图形),但由于max pooling的效果更好因此平均池化在现代CNN已经几乎被弃用。
传统的目标检测或图像分类在进行下采样的时候一般要先进行高斯模糊(高斯金字塔、拉普拉斯金字塔等多尺度特征提取方法)而在CNN中直接对feauture map进行低通滤波再最大池化,会混入过多无用信息和噪声带来的响应效果导致效果很差,因此作者提出一种巧妙的结合MaxBlurPool:
max pooling的等价表示,由于对stride=1的max响应进行的下采样导致aliasing
论文提出的MaxBlurPool
首先观察MaxPool的等价模式(结果等价但是运算量不等,没被采样到的点其实什么也没做),即使用stride=1的pooling得到输出,并在其上隔点采样得到最终的响应,如Baseline展示的那样,红色的响应直接被丢弃了,这也导致位移在不为stride的整数倍时没有连续性。既然在pooling之前增加抗混叠滤波器的效果不好,作者就尝试在隔点采样前利用一个低通滤波器对中间数据进行卷积进而将未采样到的响应信息聚合到采样点上,也可以看作是一种插值/平滑。经过Anti-aliased pooling后,feature map的cos similarity应该会有显著地提升,因为已经不像之前那样,当响应越过边界后就直接算入另一个像素,而是引入一个平滑的过渡。
通过实验证明,这一通操作确实有效,作者还对VGG-16的输出的平移不变性进行了可视化:
右键打开原图放大看,由蓝到红表示平移不变性的度量,即前述的cos similarity
这一小节没有严格的理论证明,为了做到更通俗易懂,大部分是笔者根据论文的公式/描述以及自己的理解编写的。这其实是关于DNN可解释性的一个非常有趣的话题。后续会从信号与系统/数字图像处理的角度用公式从采样定律和频域分析的角度严谨地推理关于“池化”为什么会丢失平移不变性这一问题,敬请期待。
-
正确使用padding?
padding会影响网络的平移不变性/同变性是由SiamFC(在5.4.4.4 介绍过)提出的。
其实我也没有太理解SiamFC中不使用padding的原因,论文作者认为使用padding会给特征引入位置相关性(位置编码)导致网络会“走捷径”直接根据弱边缘响应而不是特征来确定目标位置。
不过我猜测对于基础的分类任务来说,padding确实会影响平移同变性。从单层padding可能看不出来,但是随着网络的加深,卷积核的感受野不断增大,会将添加的padding(尤其是补零padding)信息聚合过来,那么处在feature map边缘的响应和处在feature map中间的响应受到padding的影响就会有所不同(显然是边缘受到的影响更大),也许这就是SiamFC中想表达的意思?
另外,由于图像不是一个在二维平面上无限伸展的信号,并且不具有周期性,因此使用循环padding虽然似乎可以提供平移同变性,但实际上会导致网络把图像认为是一个上侧/下侧循环连接,左侧/右侧循环连接的圆柱体(球体?立方体?),引入本不存在的相关性(一幅图像的天空和草地不会在相反的方向连接在一起)。
本小节暂不用正文形式,以引用形式作为TODO暂放。待笔者进一步了解后修改,若你有自己的理解欢迎email/评论交流!
最后稍微总结一下,若将CNN的输入到输出视作一个end2end的问题(不看网络中的任何一个module而将其视作一个整体,包括数据增强等trick),考虑输入进行各种变换但是输出的标签保持不变,那么卷积神经网络应该是具有这些我们期望的性质的;但是单独分析网络中的某个结构如卷积层、池化、全连接层,那么就要仔细想想了。另外,再次注意甄别平移不变性和平移同变性的区别!
一些关于CNN的 invariance性质的 paper:
Stride and Translation Invariance in CNNs
CNN: Translation Equivariance and Invariance
On Translation Invariance in CNNs: Convolutional Layers Can Exploit Absolute Spatial Location
Tracking Translation Invariance in CNNs
Why do deep convolutional networks generalize so poorly to small image transformations?
Quantifying Translation-Invariance in Convolutional Neural Networks
选出的文章都是不支持CNN拥有平移不变性和平移同变性的,这里的不支持指的是在特征层面不具有平移不变性和同变性,而非最后输出的结果。