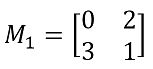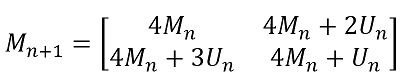数字图像处理 | 图像二值化中的规则抖动算法
前言
在只有黑色墨水的印刷机上只能搞出黑白的图形,那么问题就来了,印刷机里并没有灰色的墨,图片里的灰色阴影是怎么弄出来的?
印刷机处理灰色的方式,是通过控制区域内小墨点的密度来实现的。很好理解,如果不印任何黑点,这个区域就是白色,如果印满黑点,这个区域就是黑色,自然地,我们能推理出:印的黑点越密,显得颜色越深。在老式的报纸上能观察到这种效应。
-报纸上的图片的放大,这张报纸是通过控制墨点的大小来控制密度的-
如果墨点的大小是不变的,通过改变区域内墨点的数量,来使人看到不同的灰度,这种方法叫做图像抖动。而计算显出来的灰度和打印墨点数量之间关系的算法(抖动算法)主要有规则抖动和误差扩散抖动,由于通过规则抖动会使图像出现一些有意思的情况,故潘老师这次主要研究的是规则抖动算法。
这次写的东西在网上能找到的参考资料比较匮乏,潘老师通过自己尝试以及瞎猜,总结了一下,并且得出了一些没什么用的结果。对算法、数学恐惧或是不想动脑思考的同学可只看图片。
计算过程
规则抖动,顾名思义,可以理解为他的抖动方法是有一定规则的。规则就来自于Bayer抖动表。至于为什么叫Bayer抖动表,潘老师也不太清楚,只知道仿佛并不是叫Bayer的人发明的这个方法。这是Bayer抖动表的计算过程:
通常大家会取M3作为Bayer抖动表。为了不想看见数学式子直观的看到Bayer抖动表里面到底是什么样的,潘老师让MATLAB计算了一下M3:
用大白话解释规则抖动算法的想法:给你一个点的灰度值,在这个点的位置上要不要打印墨点?你这时候就去立刻拿来Bayer抖动表,从里面随机挑选一个数,如果挑到的数大于这个点的灰度值,就打上墨点,不然就不打。(关于灰度值的解释:灰度值越高,就越趋于白色。灰度值越低,越趋于黑色。)
这样会发生什么事呢?假设给我一个区域,这里面大多是很深的颜色(假如灰度值是10),那么我均匀地随机在Bayer抖动表里挑到的数,大部分(从11到63)都会大于这个很深的颜色(10),结果就会导致大部分点都被打上墨点,呈现的视觉效果确实是很深的颜色。
如果考虑极端情况。给我的一个区域是纯黑色。那么我在这个表里,不管怎样取数,都会大于我手里的纯黑色,所以导致,每个点都打墨点,所以就铺满了墨点就呈现黑色了。同理,给我一个纯白的区域,我在这个表里,不管怎么取数都会小于纯白色的灰度值,所以总是没有墨点打在纸上,就呈白色了。
算法思想非常简单,但是具体实现算法的时候,我们用另一种方法在抖动表里取值,方法是:用图像里的点的(x,y)坐标与抖动表的尺寸取余。具体操作的过程大概就是,随着我在图片上取点的位置一格一格移动,我在抖动表里取数的位置也在移动。对于一个足够大的区域来说,这个区域呈现的色彩可以均匀的被抖动表里所有元素“判断”一遍,在宏观上呈现预期的概率分布。通过这种方法抖动出来的图是很有特点的,如下图。也正因如此,他叫做规则抖动。
-灰阶图以及其规则抖动图,一个方格代表一个像素点。为了观察方便,图片被放大了-
还有一点,因为实际图像灰度范围是0~255,然而Bayer抖动表里的数字范围是0~63,所以对源图像还要进行范围的压缩。以下是使用MATLAB进行抖动表的生成和抖动的算法,供学有余力想要研究技术细节的同学参考。完整代码:https://github.com/divertingPan/Bayer_Dither
m1 = [[ 0 2 ];
[ 3 1 ]];
u1 = ones(2, 2);
m2 = [[ 4*m1 4*m1+2*u1 ];
[ 4*m1+3*u1 4*m1+u1 ]]
u2 = ones(4, 4);
m3 = [[ 4*m2 4*m2+2*u2 ];
[ 4*m2+3*u2 4*m2+u2 ]]
OuputM3 = 0;
for i = 1:height
for j = 1:width
ImageColor = GrayImage(i,j) / 4;
BayerMatrix = m3(bitand(i,7) + 1, bitand(j,7) + 1);
if ( ImageColor <= BayerMatrix )
OuputM3(i,j) = 0;
else
OuputM3(i,j) = 255;
end
end
end
Image8BitM3 = uint8(OuputM3);
当然,使用M4的Bayer抖动表就不需要压缩取值范围了,M4的抖动表可以做到一个实际的灰度值对应一种取值概率,即一种抖动花纹,我们也可以称其为标准图案,即每种灰度值所对应的黑白点拼出来的图案。但是实际上用M3已经足够,所以下文均以M3作为抖动表。
-4阶抖动表与3阶抖动表生成的结果相差不大-
-实际图像-
-实际图像应用抖动算法的效果-
多折腾折腾
以上是图像中只含有黑白点(二值)的情况,接下来考虑多值的(以4个值为例——白,浅灰,深灰,黑)规则抖动。潘老师没有查找到相关的资料,干脆直接用了最简单粗暴的方法,就是,将Bayer抖动表通过运算处理成3个取值域(0~21,22~43,44~63),将图形色彩也划分为对应的4个取值域,分别在各自域内做规则抖动。经过测试证明这个方法还是可以接受的。
-二值规则抖动和4值规则抖动的对比,在使用同样的Bayer抖动表的基础上,4值过渡更加平缓-
-实际图像应用的效果-
算法见代码部分。需要完整代码的请https://github.com/divertingPan/Bayer_Dither
output = zeros(height, width);
for i = 1:height
for j = 1:width
BayerMatrix1 = m3(bitand(i,7) + 1, bitand(j,7) + 1) / 3;
BayerMatrix2 = 21.3333 + BayerMatrix1;
BayerMatrix3 = 21.3333 + BayerMatrix2;
ImageColor = GrayImage(i,j) / 4;
if (ImageColor >= 0 && ImageColor < 21)
if (ImageColor > BayerMatrix1)
output(i,j) = 84;
else
output(i,j) = 0;
end
elseif (ImageColor >= 21 && ImageColor < 43)
if (ImageColor >= BayerMatrix2)
output(i,j) = 171;
else
output(i,j) = 84;
end
else
if (ImageColor >= BayerMatrix3)
output(i,j) = 255;
else
output(i,j) = 171;
end
end
end
end
潘老师知道彩色图像是由RGB三个通道组成的,每个通道实际上都是类似灰度的表达方式,但是通过某种神力,三个通道的数值合成后就成为了我们能看到的彩色。如果分别对三个通道做抖动。那么R、G、B三色就分别只有0和1的取值,排列组合,会出现8种颜色。
用一个实际的彩色图像看看效果。(算法和之前的都类似,不再列出,想要自己试一试的点击https://github.com/divertingPan/Bayer_Dither获得所有源文件。)
若是对RGB三个通道也分别进行4值抖动,那么可获得的色彩范围就更多了(4×4×4=64种),颜色也就更加准确了,算法也与灰度4值抖动相仿。
虽然放大来看图像上会有条块状纹理出现,但如果远观的话这幅图的细节已经还原出很多了。抖动算法最主要的应用价值在于他可以极大的压缩图像存储空间,主要是因为色彩空间被压缩了,原本需要256个数值表达的灰度图我甚至可以只用黑白两色表达。(在均采用PNG格式编码的条件下,测试用的原图798KB,RGB通道二值化后95.8KB,RGB通道4值化后148KB,压缩效果明显)当然如果合理看待这些条块的话,可以把他看作一种比较独特的滤镜(这样说的话,Bayer抖动表就是一种滤波器)。
【注】写推送使用的配图都是低分辨率然后放大过的,为的是各位观察方便。实际使用代码生成的图片中,上面那些图里的一个小方格就是一个图片像素点。
本来潘老师打算把这套东西都迁移到Android上以便装逼各位同学体验,但万万没想到Android中的相机和图片处理这方面是一个天坑。所以这个项目就先暂缓吧。所有MATLAB源文件都放在了GitHub上,各位可以点击“阅读原文”前往下载围观。还附带了一个processing程序,但是processing程序只做了将图像转化为4值灰度的功能。【潘老师在琢磨如何将MATLAB移植到安卓的时候发现了上次的bug,看潘老师什么时候运气好能移植成功吧,就目前看来MATLAB代码的转换也是一个天坑】