论文解析:Photo2ClipArt:Image Abstraction and Vectorization Using Layered Linear Gradients
论文 Photo2ClipArt:Image Abstraction and Vectorization Using Layered Linear Gradients 发表于ACM SIGGRAPH 2017,第一作者是来自于法国Inria的 JEAN-DOMINIQUE FAVREAU。
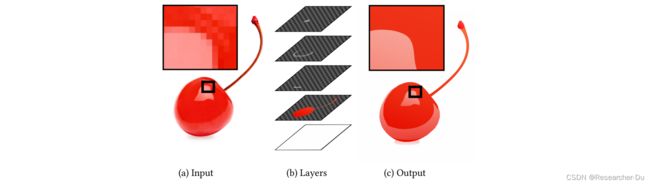
先看看论文的teaser,(a)输入是一张raster image + 对应的segmentation,(b)输出是多个线性渐变的图层,并且这些图层可以通过alpha-blending之后尽可能逼真的还原输入图像,有了多层的矢量表示,就可以很方便的图像进行编辑,如图(c)所示。

**多层矢量化的优点
经典的图像矢量化方法如Diffusion Curve,Gradient Mesh等一般将图像的所有区域均矢量化为不透明的图层,而本文将图像表示为多个半透明图层的混合,对一些图像的合成和编辑具有天然的优势。如下图所示:对于这个易拉罐的例子,只需要改变第二个黄色渐变的图层就可以实现右侧非常自然的整体颜色调整,反过来,如果是每个区域都表示为单个不透明的图层,那么下面的编辑将会非常麻烦,因为你必须要编辑很多区域才能达到相同的视觉效果。

**Liner gradient layer
本文假设每个layer的color和opacity均是线性渐变的且方向一致。关于线性渐变,下面一张图可以说明。

因此,一个layer的参数可以统一用右下角的3行4列的矩阵表示,可以看出该参数表示包含9个自由度: θ , d r , d g , d b , d α , r 0 , g 0 , b 0 , α 0 \theta, d_r, d_g, d_b,d_\alpha,r_0,g_0,b_0,\alpha_0 θ,dr,dg,db,dα,r0,g0,b0,α0。
一、问题形式化
我们的目标是对于给定的输入图像 I I I,估计一个多层的矢量化表示,其中每一个图层包括:
- 一个support domain D D D, 原始图像的像素子集,简而言之就是图层包含的范围;
- 一个颜色的线性渐变函数 C p C_p Cp (如上图所示);
- 一个不透明度的线性渐变函数 A p A_p Ap (如上图所示);
多个图层可以通过alpha blending递归的合成:
I n ( p ) = A n ( p ) C n ( p ) + ( 1 − A n ( p ) ) I n − 1 ( p ) (1) I_n(p) = A_n(p)C_n(p)+(1-A_n(p))I_{n-1}(p) \tag1 In(p)=An(p)Cn(p)+(1−An(p))In−1(p)(1)
给定一张论文中的示例:
一个包含 n n n个图层的矢量图表示为: x = ( D 1 , C 1 , A 1 , D 2 , C 2 , A 2 , . . . , D n , C n , A n ) \mathbf{x} =(D_1,C_1,A_1,D_2,C_2,A_2,...,D_n,C_n,A_n) x=(D1,C1,A1,D2,C2,A2,...,Dn,Cn,An)。为了度量矢量化的质量,作者给出了如下的能量函数:
U ( x ) = ( 1 − λ ) U fidelity ( x ) + λ U simplicity ( x ) (2) U(\mathbf{x})=(1-\lambda) U_{\text {fidelity }}(\mathbf{x})+\lambda U_{\text {simplicity }}(\mathbf{x})\tag2 U(x)=(1−λ)Ufidelity (x)+λUsimplicity (x)(2)
其中, U fidelity U_{\text {fidelity }} Ufidelity 表示重建图像与输入图像的误差,定义为:
U fidelity ( x ) = 1 ∣ I ∣ ∑ p ∈ I ∥ I ( p ) − I n ( p ) ∥ 2 2 (3) U_{\text {fidelity }}(\mathbf{x})=\frac{1}{|I|} \sum_{p \in I}\left\|I(p)-I_{n}(p)\right\|_{2}^{2}\tag3 Ufidelity (x)=∣I∣1p∈I∑∥I(p)−In(p)∥22(3)
U simplicity U_{\text {simplicity }} Usimplicity 的定义如下所示,为了鼓励算法得到更多的半透明图层,当layer为半透明时 w l = 1 w_l = 1 wl=1, 如果为不透明则 w l = 1.2 w_l=1.2 wl=1.2.
U simplicity ( x ) = 1 N ∑ l = 1 n w l (4) U_{\text {simplicity }}(\mathbf{x})=\frac{1}{N} \sum_{l=1}^{n} w_{l}\tag4 Usimplicity (x)=N1l=1∑nwl(4)
二、问题的难点
然而直接通过最小化公式(2)所示的能量化来对图像进行矢量分解几乎不可能,因为这个问题实际上是一个复杂的组合优化问题,既包含连续的优化问题(图层的线性渐变参数求解),又包含离散的优化问题(每个图层包含哪些region)。给定包含 N N N个region的一个输入图像,假设最多只有 N N N个图层,那么任意一个region可能出现或不出现在任意一个图层,因此总的配置数目为 2 N 2 2^{N^2} 2N2种,这么大的搜索空间几乎不可解。为此本文提出了一个树形搜索策略来解决这个组合优化问题。如下图所示:

原文翻译:
我们的探索从给定的初始分解开始,我们利用X-junction上的透明度假设,或要求用户指示一个或多个不透明region作为初始分解。然后,我们将这些分解扩展到相邻的未被分解的region。可以将每个新的待分解的region指定给一个或多个已有的图层,或成为一个新的图层,并为其估计线性渐变参数。 因此,我们获得了一组新region的可能分配,每个region都形成了可以进一步扩展到相邻region的分解。我们可以将这种方法生成的分解集合表示为一棵树,其中每个节点对应于一个中间分解,在expand步骤之后,中间分解分叉为多个分解。这棵树的叶子对应于所有2(N2)个可能的分解,我们的目标是在不探索整个树的情况下找到一个低能量的叶子。
我们提出了一种用于快速搜索的随机算法解空间,可以看作是蒙特卡洛树的一种形式(MCTS)。
三、Monte Carlo Tree Search

论文使用的MCTS的示意图以及伪代码如上图所示,接下来按MCTS搜索的几个步骤对本文矢量化过程进行分解。
3.1 Node selection
在树上选择一个新的节点开始扩展,每个节点 v v v对应于一个从root到 v v v的分支,实际上是一个部分分解,为了选取最优的分解进行扩展,使用了如下的函数度量:
P t → t i = exp ( − U ( x / t i ) ) 1 { t i ∈ t ⋆ } ∑ t j ∈ t ⋆ exp ( − U ( x / t j ) ) (5) P_{t \rightarrow t_{i}}=\frac{\exp \left(-U\left(\mathbf{x}_{/ t_{i}}\right)\right) \mathbb{1}_{\left\{t_{i} \in t^{\star}\right\}}}{\sum_{t_{j} \in t^{\star}} \exp \left(-U\left(\mathbf{x}_{/ t_{j}}\right)\right)}\tag5 Pt→ti=∑tj∈t⋆exp(−U(x/tj))exp(−U(x/ti))1{ti∈t⋆}(5)
需要注意的是:
- 上式表示从父节点 t t t到子节点 t i t_i ti的概率,因此从根节点到 t i t_i ti的概率表示为一连串概率的乘积,类似于: P r o o t → t i = P r o o t → t x × P t x → t y × . . . , × P t → t i P_{root \to t_i} = P_{root \to t_x} \times P_{t_x \to t_y} \times ...,\times P_{t \to t_i} Proot→ti=Proot→tx×Ptx→ty×...,×Pt→ti.
- 为了加速搜索,上式中,每一个父节点只取到能量最低的两个子节点,因此本文 ∣ t ⋆ ∣ = k = 2 |t^\star| = k = 2 ∣t⋆∣=k=2.
3.2 Expansion
扩展这棵树,如上图中间子图所示,就是不断的生长这棵树。分为两个部分:1)单个region的生长,2)基于X-junction的区域增长。前者每次只扩展一个region,后者每次同时扩展组成x-junction的4个region.
A. Singe region expansion
在已分解的region的相邻region中选择单个region进行扩展,并将这个未访问的region插入到选定节点关联的分解中。我们假设,新region可以扩展相邻区域的任何图层(图层参数不变,只是扩大范围),也可以构成一个新的单独的图层。需要注意的是,我们不考虑非相邻region的扩展,这大大减少了子节点的数量。
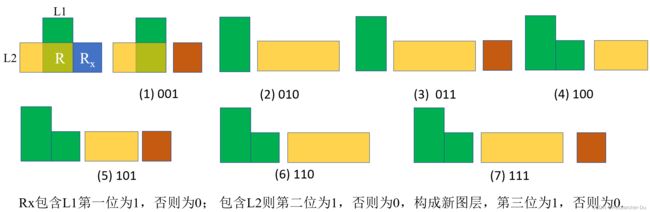
假设某个region R由M个图层混合而成,那么扩展单个region R x R_x Rx的时候,总共可能存在 2 M + 1 2^{M+1} 2M+1个子节点。因为对于 R x R_x Rx来讲,它可能位于 M + 1 M+1 M+1( M M M个已有图层,1个新生成的图层)个图层集合中的0个或多个,因此总的数目是 2 M + 1 − 1 2^{M+1}-1 2M+1−1种(全0没有任何意义)。下图给出一组示例:假设 R = L 1 ∩ L 2 R = L_1 \cap L2 R=L1∩L2, 则 R x R_x Rx可能有如下所示的 2 2 + 1 − 1 = 7 2^{2+1}-1=7 22+1−1=7种可能的情况。
B. X-junction expansion
仅适用于分解包含部分X-junction的节点,并将分解扩展到形成X-junction的所有四个region。如下图所示,我们建立在这样一个假设的基础上,即X-junction是由一个半透明图层跨越另外两个图层的边界形成的。这一假设产生了一组有限的可能解释,这取决于该X-junction中有多少个region已经被分解。

1)X-junction中没有任何region已经被分解
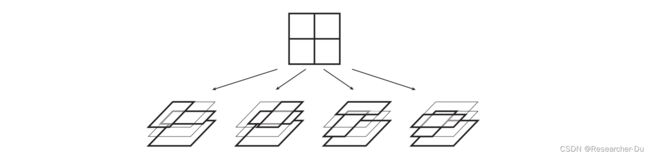
当初始化算法时,即当使用X-junction作为树根时(从某一个X-junction开始扩展,目前没有任何一个region被分解),会出现这种配置。在没有其他信息的情况下,给出一个强的假设:该X-junction是由1个半透明图层覆盖在另外两个不透明的图层上形成的,这产生了下图所示的4种可能配置:
2)X-junction中有1个或多个region已经被分解
如下所示:左图中右上角的X-junction中的region A已经被分解,右图中右侧的X-junction中的region A,B已经被分解,现在要扩展到该X-junction中其他未分解的region。

文章认为,X-junction中的4领域边界由两种情况产生:
1)单个layer没有继续扩展;
2)所有layer均扩展同时产生了一个新的layer。(如A-B,A-D之间的连接属于4邻域)。
X-junction中的8领域边界由三种情况产生:
1)有两个layer没有继续扩展;
2)有一个layer没有继续扩展并产生了一个新的layer;
3)所有的layer都扩展,同时新产生了2个layer。(如A-C之间的连接属于8邻域)。
以上述左图为例,假设region A已经被分解且是由L1, L2,L3,3个layer合成的,我们给出region B,C,D对应的configurations:
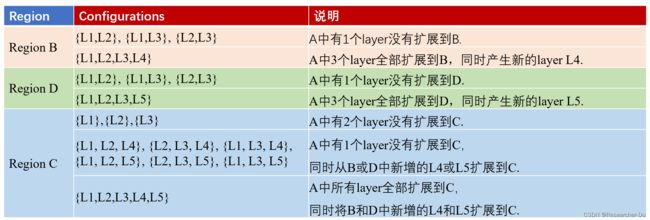
因为需要同时扩展到x-junction中所有未被分解的region,因此,B,C,D的configuration需要相互兼容,比如B是{L1,L2}, D是{L1,L3},那么C只能是L1。
以上述右图为例,假设region A,region B已经被分解且 Region A = L 1 ∩ L 2 L_1 \cap L_2 L1∩L2,Region B = L 1 ∩ L 3 L_1 \cap L3 L1∩L3. 则:
- Region C = {L1} or {L2} or {L1,L2,L4};
- Region D = {L1{ or {L3} or {L1,L3,L5};
同时也需要考虑各region 所属layer之间的兼容性:比如 Region C = {L1} 则 Region 不能是{L1},这样的话Region C 和 Region D之间不会出现明显的边界,而实际上有明显的边界。
文中重点提到:每次X-junction或单个region的扩展都最多只引入一个半透明的图层。当已有的layer扩展到当前region时不需要fit线性渐变参数,只需要对fit新引入的layer的参数。下面讲如何拟合图层的线性渐变参数。
3.3 Reward
新的layer的参数拟合如下图所示:
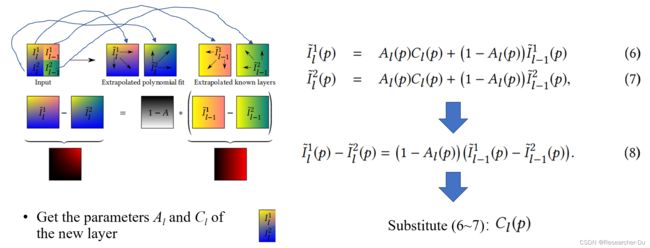
简单说明一下:这张图包含一个X-junction,本次扩展对于X-junction的扩展引入了上图左侧的两个region构成的一个layer: L l L_l Ll, 并且其他的region所包含的图层都已知, 现在我们要估计 L l L_l Ll的线性渐变参数: C l C_l Cl 和 A l A_l Al。
首先对4个region进行外插,外插结果如上图箭头所示,外插的方法是通过多项式拟合,因为目前已经知道每个region是由多少个layer组成,因此也就知道每个region的color是由几次多项式构成,因此通过拟合的方式可以求出4个region外插的颜色信息。
接下来,公式(6-7)是说 外插的图像 I ˜ l 1 \~I^1_l I˜l1 是由未知图层 与 I ˜ l − 1 1 \~I^1_{l-1} I˜l−11 合成的,外插的图像 I ˜ l 2 \~I^2_l I˜l2 是由未知图层 与 I ˜ l − 1 2 \~I^2_{l-1} I˜l−12 合成的。这两个式子相减可以消去颜色参数,因此可以解出半透明参数 A l A_l Al, 待其求解出来后,再代入(6-7)即可求解出颜色参数 C l C_l Cl。
其实,这种求解参数的方法不是唯一的解决方案。因为每次只是新增一个layer Lx,该layer以下的所有layer configuration都是已知的,那么就可以直接通过alpha-blenidng得到当前layer下方的颜色值。 为此可以将当前layer下方的所有layer合并的结果看作单个layer L1, 图像可以看作alpha blend(L1,Lx)的结果,那么就可以直接优化得到Lx的参数。
3.4 Back-propagation
最后,当node expansion结束,就可以将能量回传到父节点,并且一直递归传递直到根节点:
U ( x / t ) ← min t i ∈ t ⋆ U ( x / t i ) (9) U\left(\mathbf{x}_{/ t}\right) \leftarrow \min _{t_{i} \in t^{\star}} U\left(\mathbf{x}_{/ t_{i}}\right)\tag9 U(x/t)←ti∈t⋆minU(x/ti)(9)
注意的是,回传的时候,只把孩子节点中的能量最小值传给父节点。
参考论文
[1] Favreau J D , Lafarge F , Bousseau A . Photo2ClipArt: Image Abstraction and Vectorization Using Layered Linear Gradients[J]. Acm Transactions on Graphics, 2017, 36(6).
[2] Sun J , Liang L , Wen F , et al. Image Vectorization using Optimized Gradient Meshes[J]. ACM Transactions on Graphics, 2007, 26(3):11.
[3] Orzan A , Bousseau A , Winnemoeller H , et al. Diffusion Curves: A Vector Representation for Smooth-Shaded Images[C]// ACM. ACM, 2008:734-741.
[4] Richardt C , Lopez-Moreno J , Bousseau A , et al. Vectorising Bitmaps into Semi-Transparent Gradient Layers[C]// Computer Graphics Forum. John Wiley & Sons, Ltd, 2014.
[5] Metelli F . The perception of transparency.[J]. Scientific American, 1974, 230(4):90.
[6] Ansen D . The Art of Transparency[J]. newsweek, 2003.

