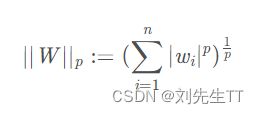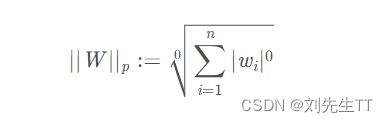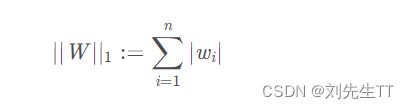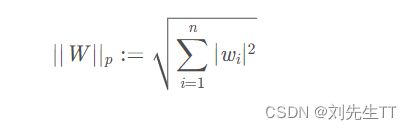NNDL 作业4 第四章作业

前言： kaggle链接，里面有本次作业需要的一些代码，以及运行过程。

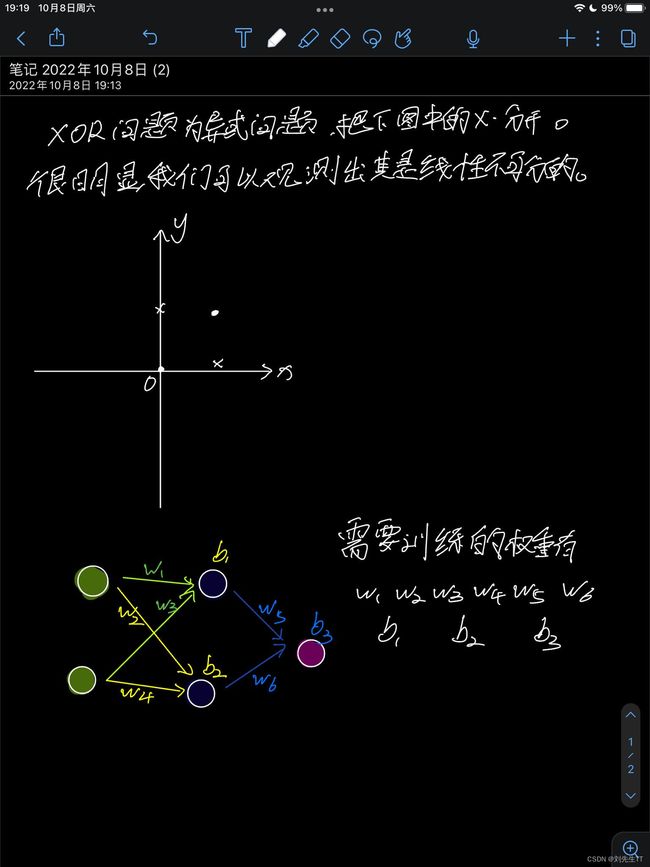
习题4-2 试设计一个前馈神经网络来解决XOR问题，要求该前馈神经网络有两个隐藏神经元和一个输出神经元，并使用RELU作为激活函数。

神经元的建立

求得权重如下

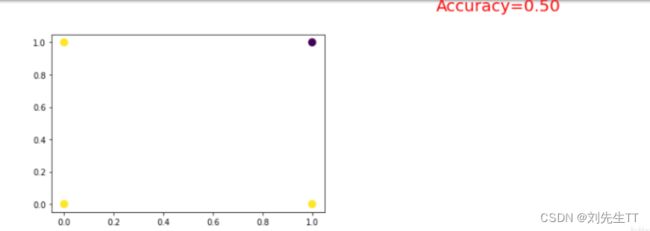
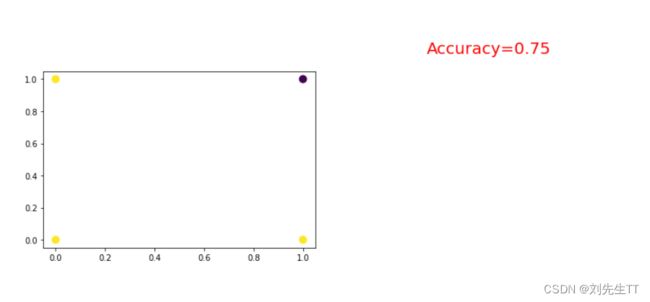
求解结果

训练次数为100次

训练次数为500次

代码如下

import torch
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt

%matplotlib inline

torch.manual_seed(1)
data = torch.tensor([[1, 0, 1], [0, 1, 1],
                 [1, 1, 0], [0, 0, 0]])
x = data[:, :2].type(torch.FloatTensor) 
y = data[:, 2].type(torch.LongTensor)
x, y = Variable(x), Variable(y)
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0)
plt.show()
class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   
        self.out = torch.nn.Linear(n_hidden, n_output)   

    def forward(self, x):
        x = F.relu(self.hidden(x))      
        x = self.out(x)
        return x
net = Net(n_feature=2, n_hidden=2, n_output=2)
print(net)
optimizer = torch.optim.Adam(net.parameters(), lr=0.01, betas=(0.9, 0.99))
loss_func = torch.nn.CrossEntropyLoss()
for t in range(50):
    out = net.forward(x)                 
    loss = loss_func(out, y)      
    optimizer.zero_grad()
    loss.backward()         
    optimizer.step()        
    
    if t % 10 == 0 or t in [3, 6]:
        plt.cla()
        _, prediction = torch.max(F.softmax(out), 1)
        pred_y = prediction.data.numpy().squeeze()
        target_y = y.data.numpy()
        plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0)
        accuracy = sum(pred_y == target_y)/4.
        plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color':  'red'})
        plt.show()
        plt.pause(0.1)

plt.ioff()
for item in net.named_parameters():
    print(item)

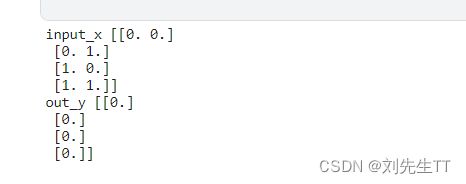
问题分析：

在训练的时候多次出现死亡Relu现象，及经过线性层处理后的数值全部为负数，最后经过relu激活全部为0.

习题 4-3试着说明死亡ReLU问题，并提出解决方法。

上面已经说了习题4-2的代码已经出现了死亡ReLU，问题，那么什么叫死亡ReLU问题呢？

死亡ReLU，说白了就是ReLU神经元死了呗，就是不再进行活动，不更新参数了。人死还有两种，饿死和饱死，而ReLU函数死亡也有两种.

“饱死”——梯度爆炸。“饿死”——梯度为0，不更新了。饿死就是上图那种。

这就是死亡relu问题，经过了激活函数后，最后的出来的值全部为0

先说说下ReLU的优点。
能够避免反向传播过程中的梯度消失、屏蔽负值、防止梯度饱和；

为什么会梯度爆炸呢？

梯度的更新公式$w^{{}^{\prime }}=w-\lambda △w$，如果我们所给学习率过大，或者初始化合理的化，最终导致梯度变化的很大，所以产生梯度爆炸现象，即饱死。

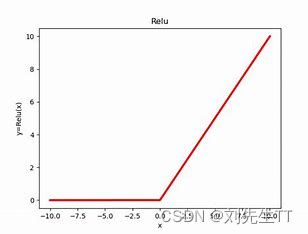
为什么会产生梯度消失呢?

我们通过观察Relu的激活函数的图像我们可以发现当自变量的值小于0时候，激活函数的值为0，激活函数的导数也为0，所以会出现梯度消失现象。

怎么解决梯度消失和梯度爆炸？

1、减小学习率
2、.使用ELU、PReLU、LeakyRelu等激活函数代替 Relu
ELU、PReLU、LeakyRelu都是让Relu在自变量小于0时函数值也是一个小于0的值，从而让w小于令0在后期有机会更新为正值。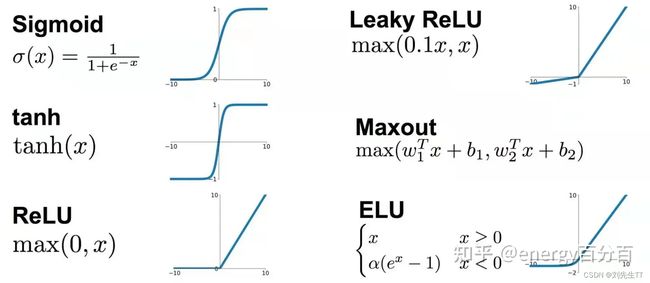

习题4-7 为什么在神经网络模型的结构化 风险函数中不对偏置b进行正则化？

一步一步分析。
通俗解释（我的理解）：
首先为什么我们需要正则化，是不是为了防止过拟合，答案是是的，而现在我们要防止过拟合，主要是防止其主要因素。线性层$y=wx+b$我们可以发现，进行大幅度仿射变换的主要是参数$w$,而$b$仅仅起到了偏移的作用。所以我们在风险函数中并未对偏置b进行正则化。
专业解释：

** 拓展 ** 神经网络常用的正则化
机器学习中正则化项常用的有L1范数、L2范数，这里我们得先了解下什么是范数（norm）。
在线性代数，函数分析等数学分支中，范数（Norm）是一个函数，代表某个向量空间（或矩阵）中的每个向量的长度或大小，使每个向量具有量化的可比较性。对于零向量，规定其长度为零。直观的说，向量或矩阵的范数越大，则我们可以说这个向量或矩阵也就越大。范数的不同计算方法使其产生了很多不同的叫法，如绝对值其实便是一维向量空间中实数或复数的范数，而Euclidean距离也是一种范数。
范数的通用定义：
设p≥0的实数,W WW为n维向量，p-norm定义为：

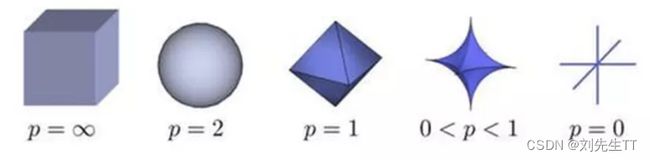
当p从∞ \infty∞到0变化时，设x为三维向量，则p-norm的三维可视化图形如下所示：

其中，当p=1时，我们称之为taxicab Norm，也叫Manhattan Norm。其来源是曼哈顿的出租车司机在四四方方的曼哈顿街道中从一点到另一点所需要走过的距离，也称为曼哈顿距离。也即我们所要讨论的L1范数，其表示某个向量中所有元素绝对值的和。
当p=2时，则是我们最为常见的Euclidean norm。也称为欧氏距离（Euclidean distance）。也即我们要讨论的L2范数。
特殊地，当p=0时，因其不再满足三角不等性，严格的说此时p已不算是范数了，但很多人仍然称之为L0范数。
这三个范数有很多非常有意思的特征，尤其是在机器学习中的正则化（Regularization）以及稀疏编码（Sparse Coding）有非常有趣的应用。 下面我们专门说一说这三个范数。
L0范数
虽然L0严格说不属于范数，我们仍然可以形式化地给出L0-norm的定义：

其表示x xx向量中所有非零元素的个数。正是L0范数的这个属性，使得其非常适合机器学习中稀疏编码，特征选择的应用。通过最小化L0范数，来寻找最少最优的稀疏特征项。但不幸的是，L0范数的最小化问题在实际应用中是NP-hard问题。因此很多情况下，L0优化问题就会被转化为更高维度的范数问题，如L1范数，L2范数最小化问题。
L1范数
当然范数中最常见，也最著名的非L2范数莫属。其应用也几乎包括科学和工程的各个领域。定义公式如下：

其应用范围非常的广泛，如在计算机视觉中的Sum of Absolute Differents，Mean Absolute Error，都是利用L1范数的定义。
L2范数当然范数中最常见，也最著名的非L2范数莫属。其应用也几乎包括科学和工程的各个领域。定义公式如下：

问题4-8 为什么在用反向传播算法进行参数学习时要采用随机参数初始化的方式而不是直接令$W=0,b=0$?

因为如果参数都设为0，在第一遍前向计算的过程中所有的隐藏层神经元的激活值都相同。在反向传播时，所有权重更新也都相同，这样会导致隐藏层神经元没有区分性。这种现象称为对称权重现象。

拓展：参数初始化的常用方法 ：
高斯分布初始化：torch.normal(means, std, out=None)生成一个以means为均值，std为标准差的正态分布。
均匀分布初始化：在一个给定的区间[-r,r]内采用均匀分布来初始化参数。超参数r的设置可以按照神经元的连接数量进行自适应的调整。

问题4-9 梯度消失问题是否可以通过增加学习率来缓解？

梯度消失问题是由于激活函数为类似于sigmoid与tanh，由于其双饱和的性质，其值太大或太小时导数都趋于0；并且在深层神经网络中，误差反向传播时，传播到前几层时梯度信息也会很小。问题是可否通过增大学习率来增大梯度，以至于梯度信息可以在更新时变大。
答案是不行，增大学习率带来的缺陷会比梯度消失问题更加严重，学习率变大时，很容易使得参数跳过最优值点，然后梯度方向改变，导致参数优化时无法收敛。

** 拓展 ** 梯度消失问题的解决方法(在前馈神经网络已经介绍了一遍，这里就当回顾了)
（1） pre-training+fine-tunning
此方法来自Hinton在2006年发表的一篇论文，Hinton为了解决梯度的问题，提出采取无监督逐层训练方法，其基本思想是每次训练一层隐节点，训练时将上一层隐节点的输出作为输入，而本层隐节点的输出作为下一层隐节点的输入，此过程就是逐层“预训练”（pre-training）；在预训练完成后，再对整个网络进行“微调”（fine-tunning）。此思想相当于是先寻找局部最优，然后整合起来寻找全局最优，此方法有一定的好处，但是目前应用的不是很多了。
（2） 梯度剪切：对梯度设定阈值
梯度剪切这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。
（3） 权重正则化
另外一种解决梯度爆炸的手段是采用权重正则化（weithts regularization），正则化主要是通过对网络权重做正则来限制过拟合。如果发生梯度爆炸，那么权值就会变的非常大，反过来，通过正则化项来限制权重的大小，也可以在一定程度上防止梯度爆炸的发生。比较常见的是 L1 正则和 L2 正则，在各个深度框架中都有相应的API可以使用正则化。
关于 L1 和 L2 正则化的详细内容可以参考我之前的文章——欠拟合、过拟合及如何防止过拟合
（4） 选择relu等梯度大部分落在常数上的激活函数
relu函数的导数在正数部分是恒等于1的，因此在深层网络中使用relu激活函数就不会导致梯度消失和爆炸的问题。
关于relu等激活函数的详细内容可以参考我之前的文章——温故知新——激活函数及其各自的优缺点（5） batch normalization
BN就是通过对每一层的输出规范为均值和方差一致的方法，消除了权重参数放大缩小带来的影响，进而解决梯度消失和爆炸的问题，或者可以理解为BN将输出从饱和区拉倒了非饱和区。

参考：

如何更快的高效的寻找最优超参数

梯度消失和梯度爆炸的解决办法

机器学习中初始化常用的方法

总结：

这次的问题相对于上次来说比较简单，大部分时间都用在了自己的拓展知识面上，对L0、L1、L2正则化系数的了解，上课讲的一下常用的激活函数的了解，例如ELU等。这次4-2问题费了我较多的时间，使用ReLU激活函数，出现了梯度消失的现象，，后来经过同学的指点迷津，我才发现。