谱聚类（Spectral Clustering）1——算法原理

简介

聚类（Clustering）是数据分析中最为广泛使用的技术之一，其广泛应用于统计学、计算机科学、生物、社会科学等。本文主要介绍一类重要的聚类算法，谱聚类（Spectral Clustering）。

谱聚类的主要思想是把所有的数据看做空间中的点。给定这些数据点之间的相似性度量，那么我们就可以构造一张相似图：如果两个点之间相似度为正（或者大于一定门限），那么它们之间就有边相连，且将其设置为边的权重。通过对相似图进行切割，让切割后不同子图之间边的权重之和尽可能低（意味着分属不同簇的点之间尽可能地不相似），而子图内边的权重之和尽可能地高（意味着同属同一簇的点之间尽可能地相似），从而达到聚类的目的。

相比传统的聚类算法，如k-means，谱聚类更容易实现，可以利用标准的线性代数软件高效求解，且往往效果更好。

 

1. 准备工作

在正式介绍谱聚类算法之前，我们需要一些必要的准备工作，以帮助我们更好地理解谱聚类算法及其背后的原理。我们先介绍图相关的一些基本概念和重要性质，然后介绍如何将数据点与图结合起来。

1.1 邻接矩阵

给定一个无向图$G=(V,E)$，其中$V=\left\{v_1,\cdots ,v_n\right\}$是顶点的集合。我们用$W$表示其邻接矩阵（Adjacency Matrix），其中
$$w_{i,j}=\{\begin{array}{rlrl}& 1\text{或权值}& ,& \text{if}(v_i,v_j)\in E\\ & 0& ,& \text{otherwise}\end{array}\text{\hspace{1em}(1-1-1)}$$
也就是说，如果顶点$v_i$和顶点$v_j$之间有边连接，$w_{i,j}$等于1（不加权的图）或者等于该边上的权值（加权图）；反之，如果顶点$v_i$和顶点$v_j$之间没有边连接，$w_{i,j}$等于0。需要注意的是，因为图$G$是一个无向图，所以$w_{i,j}=w_{j,i}$，即$W$是一个对称矩阵。

1.2 度矩阵

给定一个无向图$G=(V,E)$，我们用$D$表示其度矩阵（Degree Matrix），其中
$$d_{i,j}=\{\begin{array}{rlrl}& \sum _{j=1}^n{w}_{i,j}& ,& \text{if}i=j\\ & 0& ,& \text{otherwise}\end{array}\text{\hspace{1em}(1-2-1)}$$
为方便起见，我们将$d_{i,i}$记作$d_i$。从上式可以看出，度矩阵$D$是一个对角矩阵，即
$$D=\left[\begin{array}{cccc}{d}_1& 0& \cdots & 0\\ 0& d_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & d_n\end{array}\right]\text{\hspace{1em}(1-2-2)}$$

1.3 拉普拉斯矩阵

1.3.1 非归一化拉普拉斯矩阵

非归一化拉普拉斯矩阵（Unnormalized Laplacian Matrix）的定义为$$L=D-W\text{\hspace{1em}(1-3-1)}$$非归一化拉普拉斯矩阵$L$有很多重要的性质：
（1）对任意向量$f\in {\mathbb{R}}^n$， 我们有$$f^{T}Lf=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}(f_i-f_j{)}^2\text{\hspace{1em}(1-3-2)}$$（2）$L$是对称半正定矩阵
（3）$L$的最小特征值为0，其对应的特征向量为向量$1=[1,\cdots ,1{]}^T$
（4）$L$有$n$个非负的实数值特征值，即$0={\lambda }_1\le {\lambda }_2\le \cdots {\lambda }_n$

---

证明：
（1）
$$\begin{array}{rl}{f}^{T}Lf& =f^{T}Df-f^{T}Wf\\ & =\sum _{i=1}^n{d}_i{f}_i^2-\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{f}_i{f}_j\\ & =\frac{1}{2}\left(\sum _{i=1}^n{d}_i{f}_i^2-2\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{f}_i{f}_j+\sum _{j=1}^n{d}_j{f}_j^2\right)\\ & =\frac{1}{2}\left(\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{f}_i^2-2\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{f}_i{f}_j+\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{f}_j^2\right)\\ & =\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}(f_i-f_j{)}^2\end{array}\text{\hspace{1em}(1-3-3)}$$

（2）因为$D$和$W$都是对称矩阵，所以$L$也是对称矩阵。因为对于任意的向量$f\in {\mathbb{R}}^n$，我们都有$f^{T}Lf=\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{i,j}(f_i-f_j{)}^2\ge 0$，所以$L$是半正定矩阵。

（3）：因为$L$是对称半正定矩阵，所以其特征值非负。很显然，$L1=D1-W1=01$，所以0是$L$的最小特征值，$1$为其对应的特征向量。
（4）：由（1）-（3）可得。

---

1.3.2 归一化拉普拉斯矩阵

归一化拉普拉斯矩阵（Normalized Laplacian Matrix）的定义一般有两种：
$$L_{\mathrm{s}\mathrm{y}\mathrm{m}}=D^{-1/2}L{D}^{-1/2}=I-D^{-1/2}W{D}^{-1/2}\text{\hspace{1em}(1-3-4)}$$$$L_{\mathrm{r}\mathrm{w}}=D^{-1}L=I-D^{-1}W\text{\hspace{1em}(1-3-5)}$$其中$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$是一个对称矩阵，$L_{\mathrm{r}\mathrm{w}}$和随机游走（Random Walk）密切相关（$L_{\mathrm{r}\mathrm{w}}$不再是一个对称阵）。

和非归一化拉普拉斯矩阵$L$一样，归一化拉普拉斯矩阵$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$和$L_{\mathrm{r}\mathrm{w}}$有着和非归一化拉普拉斯矩阵$L$类似的重要性质：
（1）：对任意向量$f\in {\mathbb{R}}^n$， 我们有$$f^T{L}_{\mathrm{s}\mathrm{y}\mathrm{m}}f=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{\left(\frac{f_i}{\sqrt{d_i}}-\frac{f_j}{\sqrt{d_j}}\right)}^2\text{\hspace{1em}(1-3-6)}$$（2）：$\lambda$和$v$是$L_{\mathrm{r}\mathrm{w}}$的特征值及其对应的特征向量，当且仅当$\lambda$是$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$的特征值，且其对应的特征向量为$w=D^{1/2}v$。特别地，$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$的最小特征值为0，其对应的特征向量为向量$1=[1,\cdots ,1{]}^T$；相应的，$L_{\mathrm{r}\mathrm{w}}$最小特征值0对应的特征向量为$D^{1/2}1$。
（3）：$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$和$L_{\mathrm{r}\mathrm{w}}$是半正定矩阵（$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$是对称矩阵，$L_{\mathrm{r}\mathrm{w}}$为非对称矩阵），并且它们有$n$个非负的实数值特征值，即$0={\lambda }_1\le {\lambda }_2\le \cdots {\lambda }_n$

---

证明
（1）
$$\begin{array}{rl}{f}^T{L}_{\mathrm{s}\mathrm{y}\mathrm{m}}f& =f^{T}f-f^T{D}^{-1/2}W{D}^{-1/2}f\\ & =\sum _{i=1}^n{f}_i^2-\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}\left(\frac{f_i}{\sqrt{d_i}}\right)\left(\frac{f_j}{\sqrt{d_j}}\right)\\ & =\frac{1}{2}\left(\sum _{i=1}^n{f}_i^2-2\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}\left(\frac{f_i}{\sqrt{d_i}}\right)\left(\frac{f_j}{\sqrt{d_j}}\right)+\sum _{j=1}^n{f}_j^2\right)\\ & =\frac{1}{2}\left(\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}\frac{f_i^2}{d_i}-2\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}\left(\frac{f_i}{\sqrt{d_i}}\right)\left(\frac{f_j}{\sqrt{d_j}}\right)+\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}\frac{f_j^2}{d_j}\right)\\ & =\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{\left(\frac{f_i}{\sqrt{d_i}}-\frac{f_j}{\sqrt{d_j}}\right)}^2\end{array}\text{\hspace{1em}(1-3-7)}$$

（2）直接代入$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$和$L_{\mathrm{r}\mathrm{w}}$的定义验证即可。
（3）由（1）-（2）可得

---

1.4 相似图

上面，我们介绍了图相关的一些基本概念和重要性质。那么，如何在给定数据点及其相似性度量的前提下，得到邻接矩阵、拉普拉斯矩阵等信息呢？答案是相似图。相似图的目的在于建模数据点之间的局部邻域关系并编码点之间的相似性。一般，有三种构建相似图的方式，它们的主要区别在于如何确定数据点之间的连接关系。

1.4.1 $ϵ$-近邻图

$ϵ$-近邻图（$ϵ$-neighborhood graph），顾名思义，如果点$x_i$和$x_j$之间的距离$d_{i,j}=\Vert x_i-x_j{\Vert }_2^2$小于等于$ϵ$，则它们之间有边相连。因此，邻接矩阵$W$如下：

$$w_{i,j}=\{\begin{array}{rlrl}& ϵ& ,& \text{if}{d}_{i,j}\le ϵ\\ & 0& ,& \text{otherwise}\end{array}\text{\hspace{1em}(1-4-1)}$$

1.4.2 $k$-近邻图

直观地，如果点$x_i$在点$x_j$的$k$-近邻内，则它们之间有边相连。但是，这样得到的是一个有向图（点$x_i$在点$x_j$的$k$-近邻内不代表点$x_j$也在点$x_i$的$k$-近邻内），但是谱聚类算法针对的是无向图。一般有两种解决方式：
(1) $k$-近邻图（$k$-nearest neighbor graph）：
顾名思义，如果点$x_i$在点$x_j$的$k$-近邻内，或者点$x_j$在点$x_i$的$k$-近邻内，那么它们之间就有边相连。因此，邻接矩阵$W$如下：

$$w_{i,j}=\{\begin{array}{rlrl}& s_{i,j}& ,& \text{if}{x}_i\in KNN(x_j)\text{or}{x}_j\in KNN(x_i)\\ & 0& ,& \text{otherwise}\end{array}\text{\hspace{1em}(1-4-2)}$$

(2) 相互$k$-近邻图（mutual k-nearest neighbor graph）：
顾名思义，如果点$x_i$在点$x_j$的$k$-近邻内，同时点$x_j$在点$x_i$的$k$-近邻内，那么它们之间就有边相连。因此，邻接矩阵$W$如下：

$$w_{i,j}=\{\begin{array}{rlrl}& s_{i,j}& ,& \text{if}{x}_i\in KNN(x_j)\text{and}{x}_j\in KNN(x_i)\\ & 0& ,& \text{otherwise}\end{array}\text{\hspace{1em}(1-4-3)}$$

1.4.3 全连接图

全连接图（fully connected graph），顾名思义，在该方法下，图中的任意两点之间都有边连接。因此，邻接矩阵$W$如下：
$$w_{i,j}=s_{i,j}\text{\hspace{1em}(1-4-4)}$$由于相似图应该建模局部邻域关系，因此通常只有在相似函数本身已经编码了主要局部邻域时才选择这种构造，如高斯相似函数（高斯核函数RBF）$$s_{i,j}=\text{exp}\left(-\frac{\Vert x_i-x_j{\Vert }_2^2}{2{\sigma }^2}\right)\text{\hspace{1em}(1-4-5)}$$这里，参数$\sigma$相当于$ϵ$-近邻图中的$ϵ$，控制邻域的宽度。显然，彼此距离较近的点之间边的权重较大，而彼此距离较远的点之间边的权重较小。

---

注释：谱聚类算法对相似函数的选择，相似图的选取及其参数设置非常敏感。但是目前还没有系统性的研究，也没有一些经验规则。

---

 

2. 谱聚类算法

这部分，我们将介绍三类最常见的谱聚类算法。给定数据点$x_1,\cdots ,x_n$以及它们之间的相似性矩阵$S=(s_{i,j}{)}_{i,j=1,\cdots ,n}$，三类谱聚类算法的伪代码如下：

---

算法1：非归一化谱聚类

输入：相似性矩阵$S$，簇的数目$k$
Step1：根据1.4节方法构建相似图及邻接矩阵$W$
Step2：计算非归一化拉普拉斯矩阵$L$
Step3：计算$L$的前$k$个最小特征向量$v_1,\cdots ,v_k$
Step4：将$v_1,\cdots ,v_k$组成矩阵$V=[v_1,\cdots ,v_k]\in {\mathbb{R}}^{n\times k}$
Step5: 将$V$中的每一行向量$y_i$作为一个数据点，用k-means方法将$(y_i{)}_{i=1,\cdots ,n}$聚类成$k$簇$C_1,\cdots ,C_k$
输出：簇$A_1,\cdots ,A_k$，$A_i=\{x_j|y_j\in C_i\}$

---

算法2：归一化谱聚类
输入：相似性矩阵$S$，簇的数目$k$
Step1：根据1.4节方法构建相似图及邻接矩阵$W$
Step2：计算非归一化拉普拉斯矩阵$L$
Step3：计算广义特征值问题$Lv=\lambda Dv$的前$k$个最小特征向量$v_1,\cdots ,v_k$
Step4：将$v_1,\cdots ,v_k$组成矩阵$V=[v_1,\cdots ,v_k]\in {\mathbb{R}}^{n\times k}$
Step5: 将$V$中的每一行向量$y_i$作为一个数据点，用k-means方法将$(y_i{)}_{i=1,\cdots ,n}$聚类成$k$簇$C_1,\cdots ,C_k$
输出：簇$A_1,\cdots ,A_k$，$A_i=\{x_j|y_j\in C_i\}$

---

算法3：归一化谱聚类
输入：相似性矩阵$S$，簇的数目$k$
Step1：根据1.4节方法构建相似图及邻接矩阵$W$
Step2：计算归一化拉普拉斯矩阵$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$
Step3：计算$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$的前$k$个最小特征向量$v_1,\cdots ,v_k$
Step4：将$v_1,\cdots ,v_k$组成矩阵$V=[v_1,\cdots ,v_k]\in {\mathbb{R}}^{n\times k}$
Step5：对$V$进行归一化，使得$V$的每一行范数为1，即$v_{i,j}=\frac{v_{i,j}}{{\left({\sum }_k{v}_{i,k}\right)}^{1/2}}$
Step6: 将$V$中的每一行向量$y_i$作为一个数据点，用k-means方法将$(y_i{)}_{i=1,\cdots ,n}$聚类成$k$簇$C_1,\cdots ,C_k$
输出：簇$A_1,\cdots ,A_k$，$A_i=\{x_j|y_j\in C_i\}$

---

通过仔细观察，我们可以发现，上述三类算法基本相同，它们的主要区别在于是它们使用的拉普拉斯矩阵不同：算法1使用的是非归一化拉普拉斯矩阵$L$，算法2使用的是归一化拉普拉斯矩阵$L_{\mathrm{r}\mathrm{w}}$，而算法3使用的是归一化拉普拉斯矩阵$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$。另外，算法3多了归一化的步骤，算法1和2则不需要（目的是让结果更鲁棒，具体可以参考参考文献[1]中第7部分的内容）。我们将在下面内容解释这三个算法的区别和联系。

 

3. 从图形切割的角度去理解谱聚类算法

这部分，我们将从图形切割的角度去解释并理解谱聚类算法背后的原理。

3.1 一般的图形切割问题

如上所述，谱聚类的主要思想是把所有的数据看做空间中的点，通过对相似图进行切割，让切割后不同子图之间边的权重之和尽可能低（意味着分属不同簇的点之间尽可能地不相似），而子图内边的权重之和尽可能地高（意味着同属同一簇的点之间尽可能地相似），从而将样本点聚类为不同的簇。

我们用数学化的语言来描述该问题。假设由样本点$x_1,\cdots ,x_n$构建的相似图为$G=(V,E)$，其对应的邻接矩阵为$W$。对于任意两个不相交的顶点子集$A,B\in V$，我们定义$$\text{cut}(A,B)=\sum _{v_i\in A,v_j\in B}{w}_{i,j}\text{\hspace{1em}(3-1-1)}$$，即子集/图$A$和子集/图$B$之间边的权重之和。

因此，对于$k$-聚类问题，我们希望将图$G$划分为$k$个子集/图$A_1,\cdots ,A_k$，$A_i\cap A_j=\varnothing$，$A_1\cup \cdots \cup A_k=V$，使得$$\text{cut}(A_1,\cdots ,A_k)=\sum _{i=1}^k\text{cut}(A_i,\overline{A_i})\text{\hspace{1em}(3-1-2)}$$最小，其中$\overline{A_i}$表示子集$A_i$在集合$V$中的补集。该问题称为最小$k$-割问题。

---

注释：实际上$\text{min cut}(A_1,\cdots ,A_k)$只显式地要求不同集合之间边的权重之和尽可能低，而没有显式地要求每个子集内边的权重之和也尽可能地高。

---

对于$k=2$的情况，该最小割问题是个相对简单的问题，存在高效的解决方法。但是，实际上，这些方法往往得不到一个令人满意的结果。问题就在于该方法倾向于将一个独立的顶点与剩余顶点切分开来，如下图所示。

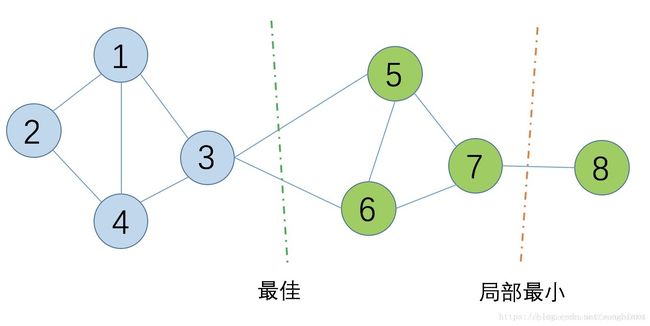
为解决该问题，直观地，我们可以在切割图形的时候将每个子集的大小考虑在内，要求每个子集的大小相对较大。

一般有两种衡量子集$A$大小的方式：

• $|A|$：$A$中点的数目
• $\text{vol}(A)$：$A$中所有边的权重之和（2倍），即$\text{vol}(A)={\sum }_{i\in A}{d}_i$

分别对应
$$\text{RatioCut}(A_1,\cdots ,A_k)=\sum _{i=1}^k\frac{\text{cut}(A_i,\overline{A_i})}{|A_i|}\text{\hspace{1em}(3-1-3)}$$$$\text{Ncut}(A_1,\cdots ,A_k)=\sum _{i=1}^k\frac{\text{cut}(A_i,\overline{A_i})}{\text{vol}(A_i)}\text{\hspace{1em}(3-1-4)}$$

值得注意的是，当所有$|A_i|$相等时，${\sum }_{i=1}^k\left(1/|A_i|\right)$取得最小值；同理，当所有$\text{vol}(A_i)$相等时，${\sum }_{i=1}^k\left(1/\text{vol}(A_i)\right)$取得最小值。因此，无论是$\text{RatioCut}$还是$\text{NCut}$，都倾向于将图划分为大小“平衡”的子图。

我们下面会看到，对$\text{RatioCut}$问题松弛就可以得到非归一化的谱聚类，对$\text{NCut}$问题松弛就可以得到归一化的谱聚类。

3.2 RatioCu问题

给定$A_1,\cdots ,A_k$，我们定义$k$个$n$维指示向量$\left\{h_1,\cdots ,h_k\right\}$，其中$h_i=[h_{i,1},\cdots ,h_{i,n}{]}^T$，来指示每个子集$A_i$由哪些点构成。具体地，
$$h_{i,j}=\{\begin{array}{rlrl}& 1/\sqrt{|A_i|}& ,& \text{if}j\in A_i\\ & 0& ,& \text{otherwise}\end{array}\text{\hspace{1em}(3-2-1)}$$
也就是说，如果第$j$个点属于子集$A_i$，那么$h_{i,j}=1/\sqrt{|A_i|}$；否则，$h_{i,j}=0$。值得注意的是，$h_i^T{h}_i=1$，而$h_i^T{h}_j=0,\forall i\ne j$，即$\{h_i{\}}_{i=1,\cdots ,k}$之间彼此正交。

由式(1-3-3)可知，
$$\begin{array}{rl}{h}_i^{T}L{h}_i& =\frac{1}{2}\sum _m\sum _n{w}_{m,n}{\left(h_{i,m}-h_{i,n}\right)}^2\\ & =\frac{1}{2}\left[\sum _{m\in A_i}\sum _{n\in \overline{A_i}}{w}_{m,n}{\left(\frac{1}{\sqrt{|A_i|}}-0\right)}^2+\sum _{m\in \overline{A_i}}\sum _{n\in A_i}{w}_{m,n}{\left(0-\frac{1}{\sqrt{|A_i|}}\right)}^2\right]\\ & =\frac{1}{2}\left(\sum _{m\in A_i}\sum _{n\in \overline{A_i}}{w}_{m,n}\frac{1}{|A_i|}+\sum _{m\in \overline{A_i}}\sum _{n\in A_i}{w}_{m,n}\frac{1}{|A_i|}\right)\\ & =\frac{1}{2}\left(\frac{\text{cut}(A_i,\overline{A_i})}{|A_i|}+\frac{\text{cut}(A_i,\overline{A_i})}{|A_i|}\right)\\ & =\frac{\text{cut}(A_i,\overline{A_i})}{|A_i|}\end{array}\text{\hspace{1em}(3-2-2)}$$
我们将其扩展成矩阵的形式。令$H=[h_1,\cdots ,h_k]\in {\mathbb{R}}^{n\times k}$，
$$\begin{array}{rl}{\left(H^{T}LH\right)}_{i,i}& =h_i^{T}L{h}_i\end{array}\text{\hspace{1em}(3-2-3)}$$因此，
$$\begin{array}{rl}\text{RatioCut}(A_1,\cdots ,A_k)& =\sum _{i=1}^k\frac{\text{cut}(A_i,\overline{A_i})}{|A_i|}\\ & =\sum _{i=1}^k{h}_i^{T}L{h}_i\\ & =\sum _{i=1}^k{\left(H^{T}LH\right)}_{i,i}\\ & =Tr\left(H^{T}LH\right)\end{array}\text{\hspace{1em}(3-2-4)}$$
其中$Tr$表示矩阵的迹（Trace）。

因此，原最小化$\text{RatioCut}(A_1,\cdots ,A_k)$问题等价于下述问题：
$$\begin{array}{rl}\underset{H}{\min }& Tr\left(H^{T}LH\right)\\ s.t.& H^{T}H=I\end{array}\text{\hspace{1em}(3-2-5)}$$由于$H$满足式(3-1-1)，其每个元素的取值只能为0或者$1/\sqrt{|A_i|}$，因此上述问题(3-2-5)是一个NP-hard问题。

幸运的是，我们可以对上述问题(3-2-5)进行松弛，即允许矩阵$H$可以为任意实数矩阵，从而将其转化为标准的迹最小化问题。Rayleigh-Ritz定理告诉我们，$Tr\left(H^{T}LH\right)$的最小值为$L$的$k$个最小特征值之和，相应的最优解$H$为$L$的$k$个特征向量组成的矩阵（每个特征向量为$H$的每一列，即第2部分谱聚类算法1中的$V$）。

但是，松弛后求解得到的$H$并不能直接指示聚类的结果，因为此时的$H$是实数值，而不是离散值。所以谱聚类算法在最后一步会对$H$（伪代码中的$V$）做一个$k$-means聚类：将$H$（$V$）中的每一行看作一个点，这样一共有$n$个点。我们对这$n$个点做一个$k$-means聚类，就可以得到最终的聚类结果。如何理解？其实计算$H$（$V$）就像PCA中的降维操作，我们将原本$n$维空间中的$n$个点降维成了$k$维空间中$n$个点，但是保留了这些数据点最重要的特征。这也是为什么谱聚类比一般的$k$-means效果好的原因所在。可能还有人问，$k$-means之外的聚类算法可不可以。答案是肯定的。

3.3 Ncut问题

和RatioCut类似，我们定义$k$个$n$维指示向量$\left\{h_1,\cdots ,h_k\right\}$来指示$A_1,\cdots ,A_k$，其中$h_i=[h_{i,1},\cdots ,h_{i,n}{]}^T$。不同的是，
$$h_{i,j}=\{\begin{array}{rlrl}& 1/\sqrt{\text{vol}(A_i)}& ,& \text{if}j\in A_i\\ & 0& ,& \text{otherwise}\end{array}\text{\hspace{1em}(3-3-1)}$$
参照公式(3-2-2)-公式(3-2-4)的推导，我们可以得到类似的结果
$$h_i^{T}L{h}_i==\frac{\text{cut}(A_i,\overline{A_i})}{\text{vol}(A_i)}\text{\hspace{1em}(3-3-2)}$$$$\text{NCut}(A_1,\cdots ,A_k)=Tr\left(H^{T}LH\right)\text{\hspace{1em}(3-3-3)}$$
因此，我们的优化目标还是$Tr\left(H^{T}LH\right)$，但是现在$H^{T}H\ne I$，而是$H^{T}DH=I$。
$$\begin{array}{r}(H^{T}DH{)}_{i,i}=h_i^{T}D{h}_i=\sum _{j\in A_i}{d}_j{h}_{i,j}^2=\sum _{j\in A_i}{d}_j\frac{1}{\text{vol}(A_i)}=\frac{\text{vol}(A_i)}{\text{vol}(A_i)}=1\end{array}\text{\hspace{1em}(3-3-4)}$$$$\begin{array}{r}(H^{T}DH{)}_{i,j}=h_i^{T}D{h}_j=\sum _{l=1}^n{d}_l{h}_{i,l}{h}_{j,l}=0\end{array}\text{\hspace{1em}(3-3-5)}$$
我们令$H=D^{-1/2}F$，显然有$F^{T}F=I$。

所以，原最小化$\text{NCut}(A_1,\cdots ,A_k)$问题等价于下述问题：
$$\begin{array}{rl}\underset{F}{\min }& Tr\left(F^T{D}^{-1/2}L{D}^{-1/2}F\right)\\ s.t.& F^{T}F=I\end{array}\text{\hspace{1em}(3-3-6)}$$忽略$F$的约束，上述问题(3-3-6)相当于求解$D^{-1/2}L{D}^{-1/2}$（即$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$）的$k$个最小特征值及其对应的特征向量（第2部分谱聚类算法3中的$V$）。实际上，如果我们回顾一下1.3.2节$L_{\mathrm{s}\mathrm{y}\mathrm{m}}$和$L_{\mathrm{r}\mathrm{w}}$的关系我们可以发现，$H$对应的是$L_{\mathrm{r}\mathrm{w}}$的$k$个最小特征值对应的特征向量组成的矩阵（第2部分谱聚类算法2中的$V$）。

最后，再对$H$进行$k$-means聚类或其他聚类即可。

3.4 总结及拓展

最后，对这一部分做个总结及拓展。

3.4.1 与最优解的差？

如上所述，谱聚类算法相当于RatioCut或Ncut问题的松弛解，我们希望该松弛解足够地好，即与最优解之间的gap能被bound住。可惜的是，不存在这样的一个bound。

我们看下图一个例子。假设我们要对下图进行2割以最小化RatioCut。最优解应该是$A=\{V_1,\cdots ,V_k,V_{2k+1},\cdots ,V_{3k}\}$，$\bar{A}=\{V_{k+1},\cdots ,V_{2k},V_{3k+1},\cdots ,V_{4k}\}$，此时$\text{RatioCut}=\{A,\bar{A}\}=2/k$。但是谱聚类算法得到的解为$B=\{V_1,\cdots ,V_k,V_{k+1},\cdots ,V_{2k}\}$，$\bar{B}=\{V_{2k+1},\cdots ,V_{3k},V_{3k+1},\cdots ,V_{4k}\}$，此时$\text{RatioCut}=\{B,\bar{B}\}=1$，足足是最优解的$k/2$倍。

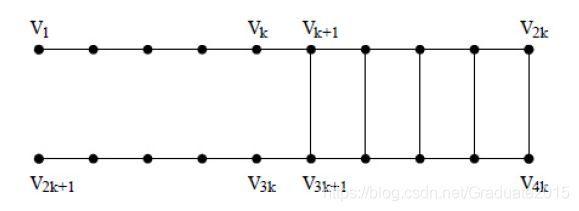
谱聚类算法吸引我们的在于其简单、高效。

3.4.2 RatioCut or Ncut？

参考文献[1]推荐Ncut，或者说推荐使用归一化的拉普拉斯矩阵，而且更推荐使用$L_{\mathrm{r}\mathrm{w}}$。

为什么推荐使用Ncut或者说归一化的拉普拉斯矩阵？理由也很直接明白。我们以$k=2$来进行说明。我们在第3部分的最开始曾提到，我们希望让切割后不同子图之间边的权重之和尽可能低（意味着分属不同簇的点之间尽可能地不相似），而子图内边的权重之和尽可能地高（意味着同属同一簇的点之间尽可能地相似）。其实，我们是有两个目标的：
（1）分属不同簇的点之间尽可能地不相似，也就是不同子图之间边的权重之和尽可能低，即${\sum }_{i\in A,j\in \bar{A}}{w}_{i,j}$尽可能地小；
（2）同属同一簇的点之间尽可能地相似，也就是同一子图内边的权重之和尽可能地高，即${\sum }_{i,j\in A}{w}_{i,j}$和${\sum }_{i,j\in \bar{A}}{w}_{i,j}$都尽可能地大。

毋庸置疑，RatioCut和Ncut都有直接包含目标（1）。差别在于Ncut也直接包含了目标（2）。我们可以发现：
$$\begin{array}{rl}\sum _{i,j\in A}{w}_{i,j}& =\sum _{i\in A,j\in A\cup \bar{A}}{w}_{i,j}-\sum _{i\in A,j\in \bar{A}}{w}_{i,j}\\ & =\text{vol}(A)-\text{cut}(A,\bar{A})\end{array}\text{\hspace{1em}(3-4-1)}$$我们发现，Ncut是希望$\text{cut}(A,\bar{A})$尽可能小，而$\text{vol}(A)$尽可能大，此时${\sum }_{i,j\in A}{w}_{i,j}$也是尽可能大的。${\sum }_{i,j\in \bar{A}}{w}_{i,j}$同理。

所以，从上述这点来说，我们更倾向使用Ncut或者说归一化的拉普拉斯矩阵。另外，从一致性问题考虑，也是支持这一结论。

---

注释：另一种MinMaxCut问题则直接在其优化目标中体现了上述目标（2）
$$\text{MinMaxCut}(A_1,\cdots ,A_k)=\sum _{i=1}^k\frac{\text{Cut}(A_i,\overline{A_i})}{{\sum }_{i,j\in A}{w}_{i,j}}\text{\hspace{1em}(3-4-2)}$$

---

为什么推荐使用$L_{\mathrm{r}\mathrm{w}}$？原因在于$L_{\mathrm{r}\mathrm{w}}$的特征值在计算上更鲁棒。

Reference

[1]: Luxburg, U. V. . “A Tutorial on Spectral Clustering.” Statistics and Computing 17.4(2004):395-416.
[2]: https://www.cnblogs.com/pinard/p/6221564.html