量子笔记：全局相位、相对相位、布洛赫球面
目录
0. 概要
1. 全局相位
2. 相对相位
3. 布洛赫球面
4. 布洛赫球面坐标与笛卡尔坐标的转换
5. 3种基底
6. 布洛赫球、纯态与混合态
0. 概要
量子计算、量子信息、量子编程自学笔记系列。
用自己能看懂的方式来表述对于量子计算基础知识的理解。
不求体系完备和逻辑严谨、但求通俗易懂。或能顺便给路过的小伙伴一些参考和启发那是纯属巧合概不认账^-^。当然，这里仅限于轮廓的勾勒和要点的连接，对细节感兴趣的话还是要找正经的参考书。
本节介绍全局相位以及量子态的等价性，相对相位，以及基于布洛赫球面的量子态的表示。
1. 全局相位
任意一个量子比特的状态可以表达为两个基态（通常取计算基底的两个基向量）的叠加态，如下所示：
考虑另一个量子态 
，对
进行观测我们会发现，它坍缩到
和坍缩到
的概率仍然分别是
和
，与对
进行观测的坍缩概率是相同的！
换句话说，从观测的角度来说，和是不可区分的。或者说，
是不可观测的。被称为全局相位因子（global phase factor），相应地
被称为全局相位。
当两个量子态之间只相差一个全局相位因子（比如说上述 和），（因为它们从观测上是不可区分的），它们被认为是相同的或者说等价的。
2. 相对相位
仍然考虑，由于a和b均为复数，它们分别可以表示为
，
，其中，
。
进一步，由上一节的结论可知（用
表示量子态的等价）：
其中，
被称为相对相位。目前我们还不知道相对相位有什么意义，到讨论干涉（interference）的时候就能看出相对相位的重要性了。
3. 布洛赫球面
到目前为止所讨论的量子比特的叠加态表示是在复希尔伯特空间
中的表示，（可视为
)相当于4维空间。对于生活在3维空间的我们来说，这种表示法的一个不好的地方是难以进行可视化处理。但是这个当然难不住科学家们。。。
基于以上两节的讨论，我们知道，量子态表示的自由度并不是4。由于
的约束，量子态可视为分布在 （可视为)中单位超球面上的点，因此可以通过非线性投影的方式映射到
中的单位球面上来。其中的关键要点是：忽视全局相位；换句话说，将所有相差
倍的量子态视为同一的量子态。
基于上一节的讨论，我们知道了量子态可以表示为
由于 
，所以总能找到某个
，使得：
这样，我们就可以得到另一种量子态的表示方式：
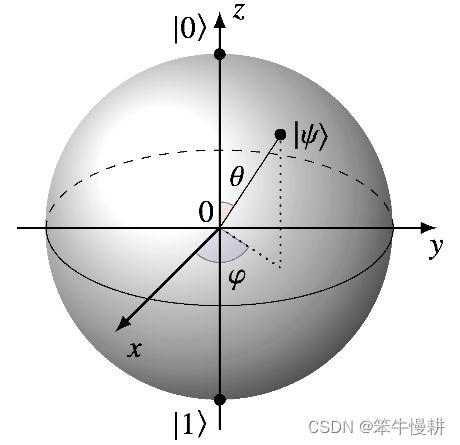
这样，每一个由
决定的量子态可以映射到三维空间的单位球面的一个点。如下图所示，这样的单位球面称为布洛赫球面，得名于物理学家利克斯.布洛赫（因为核磁共振方面的研究而获得1962年的诺贝尔物理学奖）。
图1 布洛赫球面
By convention, 以单位球面与z轴正向交点（俗称北极点）代表，以另一端的交点（南极点）代表。
4. 布洛赫球面坐标与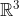笛卡尔坐标的转换
如上所示，表示量子态的点（向量）落在布洛赫球面上，由表示，球面到远点的距离为1，因此可以视为由球坐标
表示的点，对应的笛卡尔坐标如下所示：
对应的布洛赫球面坐标为
，笛卡尔坐标为
.
对应的布洛赫球面坐标为
，笛卡尔坐标为
.
5. 3种基底
由上面两节讨论可知，计算基底
的两个基向量分别对应布洛赫球面的北极点和南极点。
同样的，
球面与x轴的两个交点所代表的向量也构成一组标准正交基，记为
，称为阿达马（或哈达玛，Hadamard）基底
球面与y轴的两个交点所代表的向量也构成一组标准正交基，记为
，称为圆基底
这是量子计算中常用的三种基底，它们的各种表示汇总如下所示：
6. 布洛赫球、纯态与混合态
布洛赫球（Bloch ball）是布洛赫球面的扩充。
在布洛赫球面上的点表示的量子态称为纯态，而出现在球内的点（离球心距离<1的点）所表示的量子态称为混合态（mixed state）。球心该点所代表的量子状态是最大混合态（maximally mixed state）。
混合态相关不甚了解。。。就不瞎装了。。。先补课后再来补充。
相关博文：
量子笔记：酉矩阵（幺正矩阵）、量子门的可逆性
量子笔记：量子比特的表示
参考文献：
[1] 罗伯特.S.苏托尔 著，吴攀译：与量子比特共舞，人民邮电出版社
[2] 克里斯.伯恩哈特 著，邱道文 周旭 等译：人人可懂的量子计算
[3] 布洛赫球面_百度百科 (baidu.com)