机器学习学习笔记——以波士顿房价问题为例

前言

说起入坑机器学习，还是因为在学校一个偶然的机会：那时候在我们教三楼验收数据库课设，然后去学办逛了逛，就看到了有一个百度菁英俱乐部的创立请求书，然后觉得百度这个头衔听牛批的，并且主席刚好是我的一个朋友，然后就找到了他，当天中午去参加了面试（没有走后门嗷），还是正经的写了简历和做了题目的，然后一个研究生学长面试我们（我也比较熟），由于想学技术，就选了技术部，刚好他问的问题我都有所了解，然后就顺利通过了面试。（难道这个俱乐部就是为我准备的？哈哈哈）。后面就开始学了，部门里每周都会安排培训，讲解一些学习过程中的核心内容，然后平时的课余时间就是看书，看视频入门，总之刚开始的时候是极其的枯燥乏味，并且有的书会经常讲一些数学公式啥的，由于之前学的高数、概率论、线代啥的忘得差不多了，理解起来非常的吃力。后面逛了逛知乎和一些前辈的博客，我了解到，刚入门的时候是没有必要一下子搞懂所有数学推导公示的，就算你懂了，花费了大量的时间不说，不能实时应用，学了没多一会儿就容易忘了，这不是在做无用功。所以我们只需要了解机器学习是干啥的，有哪些方法/算法可以用于实现机器学习，这些方法的思想是什么，这么多方法，我们应该怎么选择合适的算法去实现，如何评价机器学习算法模型的优劣等等知识，让你的脑子里有一个大体的运用机器学习解决一些问题的框架就行，并且你还不用了解的特别深入，毕竟这只是入门而已，刚开始学的太多，不然就是“机器学习从入门到放弃”了。

什么是机器学习？

以下是百度百科里面对机器学习的定义：

机器学习是一门多学科交叉专业，涵盖概率论知识，统计学知识，近似理论知识和复杂算法知识，使用计算机作为工具并致力于真实实时的模拟人类学习方式， 并将现有内容进行知识结构划分来有效提高学习效率。

简单来说，机器学习是从现有的数据中自动分析获得一个或多个模型，再通过这个模型对未知的数据进行预测。这很像我们人类学习知识的过程，先在一堆乱七八糟的数据里面寻找一些规律，通过这些规律去解决其他问题，就是老师经常说的“举一反三”，包括你解数学题，先跟着老师解一个题，后面你再去做家庭作业做其他类似的题。

机器学习分类

一般分为两类：监督学习和无监督学习
而监督学习又分为回归和分类问题
无监督学习分为聚类和关联分析

监督学习

百度百科定义：

利用一组已知类别的样本调整分类器的参数，使其达到所要求性能的过程，也称为监督训练或有教师学习。
监督学习是从标记的训练数据来推断一个功能的机器学习任务。训练数据包括一套训练示例。在监督学习中，每个实例都是由一个输入对象（通常为矢量）和一个期望的输出值（也称为监督信号）组成。监督学习算法是分析该训练数据，并产生一个推断的功能，其可以用于映射出新的实例。一个最佳的方案将允许该算法来正确地决定那些看不见的实例的类标签。这就要求学习算法是在一种“合理”的方式从一种从训练数据到看不见的情况下形成。

监督学习需要人为的操作，为我们的数据添加标记，通过这些标记来训练我们的模型，标记的选择和添加对模型的好坏有着很大的影响。说白了就是我们教机器怎么做事，他根据我们给出的解决问题方法（模型）来解决其他的问题。

回归

回归：从一组数据出发，确定某些变量之间的定量关系式；即建立数学模型并估计未知参数。
回归的目的是预测数值型的目标值，它的目标是接受连续数据，寻找最适合数据的方程，并能够对特定值进行预测。这个方程称为回归方程，而求回归方程显然就是求该方程的回归系数，求这些回归系数的过程就是回归。

回归问题的目标值是连续的数据，这跟我们高中所学习的回归问题有异曲同工之妙。不过高中所学习的回归问题大都比较简单，一般都是线性的。机器学习中的回归问题不只是普通的求解一个回归方程而已，后面还需要大量的工作来实现模型的优化检验等一系列问题。

分类

分类就是在已有数据的基础上学习出一个分类函数或构造出一个分类模型，这就是通常所说的分类器。该函数或者模型能够把数据集中的样本x映射到某个给定的类别y，从而用于数据预测。

分类问题的预测值（目标值）是离散的数据。就是把一组数据值归类嘛，像是识别某个图片是不是猫，一组图片是、一组不是，不就是分类问题嘛。分类有两步：第一步，分析数据集特点创建分类模型（选用适合的算法）；第二步，使用构建好的模型测试数据集，评估这个模型的好坏，选择分类效果好的模型。
监督学习常用算法有：线性回归、逻辑回归、高斯判别分析、朴素贝叶斯、决策树、神经网络、支持向量机、协同过滤等。

无监督学习

百度百科定义：

现实生活中常常会有这样的问题：缺乏足够的先验知识，因此难以人工标注类别或进行人工类别标注的成本太高。很自然地，我们希望计算机能代我们完成这些工作，或至少提供一些帮助。根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题，称之为无监督学习。

无监督学习就跟监督学习相反，很多情况下，我们也不知道这个问题应该有一种什么模型来解决，也不知道这类问题之间的数据有什么关联或者说他们之间的关联很难表示出来，这时候我们就希望通过某一种或几种特定的模型来让计算机得到其中的关系。这更像是自学，没有老师教。
这跟我们平时考试做题差不多，监督学习像是那些有标准答案的科目，我们通过答案来分析解决这一类问题；而无监督学习则像是没有标准答案，我们根据自己的知识储备来解决这些问题，可能效果很好，也可能不尽如人意。

聚类

聚类就是将数据集划分为由若干相似实例组成的簇的过程，使得同一个簇中实例间的相似度最大化，不同簇中实例间的相似度最小化。也就是说，一个簇就是由彼此相似的一组对象所构成的集合，不同簇中的实例通常不相似或相似度很低。聚类是由样本间相似性的度量标准将数据集自动划分为几个簇，簇是怎么样的没有事先的定义，而是根据实际数据的特征按照数据之间的相似性来定义的。就像是老话说的“物以类聚，人以群分”。聚类分析算法的输入是一组样本及一个度量样本间相似度的标准，输出是簇的集合。

一个小例子

波士顿房价预测

我们借助sklearn这么一个基于python语言的机器学习工具，用机器学习方法来简单的预测一下波士顿房价的走向。

1.导入数据

sklearn.datasets

• 加载获取流行数据集
  • datasets.load_*()
    获取小规模数据集，数据包含在datasets里
  • datasets.fetch_*(data_home=None)
    获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录,默认是 ~/scikit_learn_data/
  • load和fetch返回的数据类型datasets.base.Bunch(字典格式)

其中一般：

• data：特征数据数组，是 [n_samples * n_features] 的二维 numpy.ndarray 数组
• target：标签数组，是 n_samples 的一维 numpy.ndarray 数组
• DESCR：数据描述
• feature_names：特征名,新闻数据，手写数字、回归数据集没有
• target_names：标签名
  首先我们从sklearn中导入有关波士顿房价的数据

from sklearn.datasets import load_boston
data = load_boston()
print("data\n",data)

这里截图了一小部分数据：

其中data是数据集，target是目标值。
然后我们通过查找data里面的feature值也就是影响房价的特征值’CRIM’, ‘ZN’, ‘INDUS’, ‘CHAS’, ‘NOX’, ‘RM’, ‘AGE’, ‘DIS’, ‘RAD’,‘TAX’, ‘PTRATIO’, ‘B’, 'LSTAT’房价是由这么几个因素控制的，其中的RM可能指的是房间数，然后我们就先以一个影响因素来模拟房间数对波士顿房价的变化趋势并进行预测。

2.绘制散点图

代码如下：

room_index = 5
X, y = data['data'], data['target']
X_rm = X[:, room_index]
plt.scatter(X_rm, y)
plt.show()

由于我们是研究房间数这一个影响因素，所以在target中选择第六个变量RM，然后再列表中他的下标是5，我们分别用x和y提取出data中的具体数据，总的数据都是以字典的形式储存的，然后每一个键值里面是数组，我们将数组中的RM值作为x轴坐标，target目标值作为y轴绘制散点图如下所示：

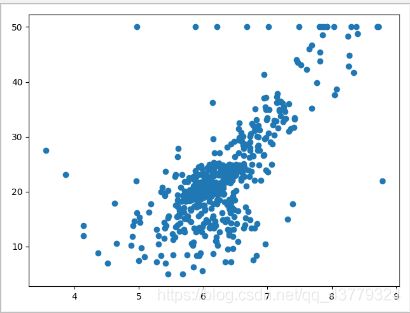
3.回归分析

通过这一系列散点图，我们的目标是找到一条能更好的预测房间数与房屋价格之间关系的线性函数。
首先我们能想到的方法是随便找到一条直线，通过计算机的matplotlib库来绘制散点图和所给直线之间的拟合程度。

import random
def f(x):
    k = random.randint(-50, 50)
    b = random.randint(-50, 50)
    return k * x + b
plt.scatter(X_rm, y)
plt.plot(X_rm, f(X_rm), color='red')

通过python中的random函数在一定范围内随机生成直线方程的k、b值，然后构造直线并在图中绘制出来，以下就是一条随机生成的直线。

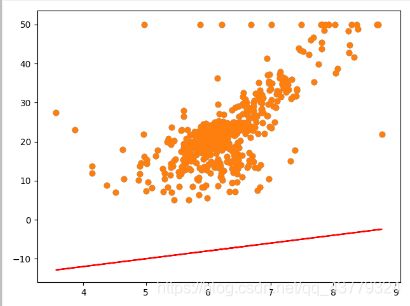
这种方法可以是可以，但是你肯定会觉得他好呆，随机找直线的各种组合实在是太多了，并且当中的很多直线完全不沾边，虽然计算机的计算能力很强，但是如果数据太多的话，这样是非常的浪费资源的。如果我们有一个方法能够实时的显示这个kb值所表示的直线与已知数据的契合程度的话就很方便了，这个时候就有了损失函数这个东东，用于定量的计算kb值所表示的函数的预测结果好不好。这里我们就用到了平方损失函数：

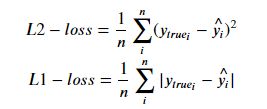
其中y_true表示数据集里面真实的数据，y^表示通过这个模型模拟出来的函数所预测出来的数据，真实数据-预测数据平方之后求和，然后求平均值，用于检验这个函数的预测效果好不好，如果这个值比较小的话就表示预测效果好，反之不好。

4.减小误差

上面已经提到了使用损失函数来定量的表示我们生成的函数的误差，从而找到更好的模型能够预测房价随房间数的变化。虽然已经找到了评价方式，但是还有一个问题就是，目前我们还是使用随机数的方法找到一个k、b值，然后带入参加计算，这显得有点呆，毕竟我们是在学人工智能哎！所以该用怎样的方式来让计算机更好的选取k、b的值呢？
这里我们用到了数学上面的一个方法，首先我们观察上面给出的L₂_loss这个损失函数，我们的目的就是要让k、b着两个变量的变化不是每次都随机的产生，而是根据当前的情况做出一个判断，然后科学的改变k、b的值，使之每次都能使损失值减少。那么应该用怎样的标准去判断呢？看这个式子，他是一个二次函数，我们的目的是取得这个函数的极小值，图像上每一点切线的斜率表示的就是k，在对称轴的左边，我们要增大k使之接近极值点；反之要减小k接近极值点。运用数学里面的知识，我们就可以选择求k的偏导数，找到k的变化情况，求取k的合适取值，同理求b。以下的公式我列举了几个主要的公式分别求取k和b的偏导。

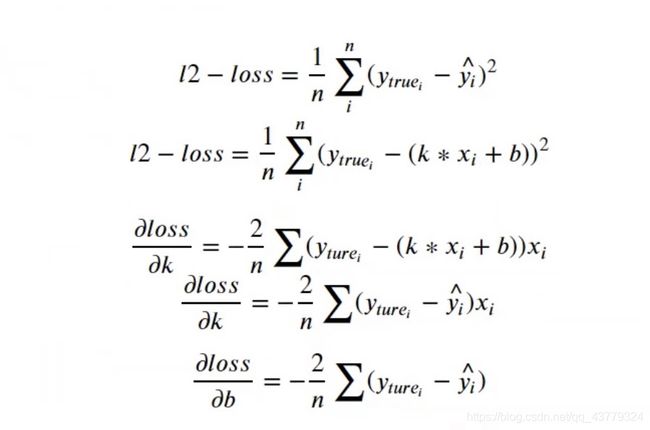
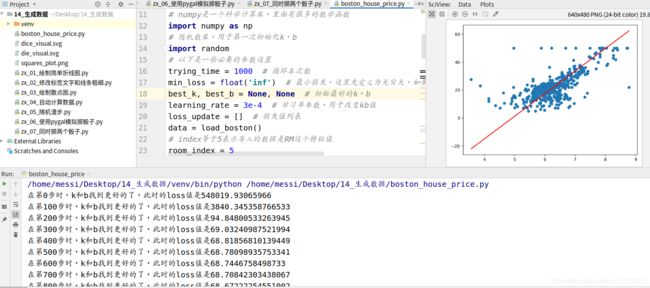
具体代码如下，已经详细给出了每一步的注释，应该看的懂。

# 从sklearn中导入boston房价数据集
from sklearn.datasets import load_boston
# 导入matplotlib库用于画图
import matplotlib.pyplot as plt
# numpy是一个科学计算库，里面有很多的数学函数
import numpy as np
# 随机数库，用于第一次初始化k，b
import random
# 以下是一些必要的参数设置
trying_time = 10000  # 循环车次数
min_loss = float('inf')  # 最小损失，这里先定义为无穷大，如果后面计算的损失比这个小就赋值给这个
best_k, best_b = None, None  # 初始最好的k，b
learning_rate = 3e-4  # 学习率参数，用于改变kb值
loss_update = []  # 损失值列表
data = load_boston()
# index等于5表示导入的数据是RM这个特征值
room_index = 5
X, y = data['data'], data['target']
X_rm = X[:, room_index]
# 初始化k，b的值
k = random.randint(-100, 100)
b = random.randint(-100, 100)
# 计算预测房价
def f(x):
    return random.randint(-100, 100) * x + random.randint(-100, 100)
# 计算预测房价
def price(x, k, b):
    return k * x + b
# 求k的偏导
def partial_k(ytrue,yhat,x):
    return -2 * np.mean((np.array(ytrue) - np.array(yhat)) * np.array(x))
# 求b的偏导
def partial_b(ytrue, yhat):
    return -2 * np.mean(np.array(ytrue) - np.array(yhat))
# 计算损失值
def l2_lose(y, yhat):
    return np.mean((np.array(y)-np.array(yhat))**2)
# 循环计算找到更好的k，b值
for i in range(trying_time):
    # learning_rate = np.exp(-i)
    # 求出预测值
    yhat = price(X_rm, k, b)
    # 求出损失值
    l2 = l2_lose(y=y, yhat=yhat)
    # 判断当前损失值是否小于最小损失
    if l2 < min_loss:
        # 更新最小损失
        min_loss = l2
        # 更新更好的k，b值
        best_k, best_b = k, b
        loss_update.append([i, l2])
        if i % 100 == 0:
            print('在第{}步时，k和b找到更好的了，此时的loss值是{}'.format(i,l2))
    # 求偏导用于计算更好的k，b值
    gradient_k = partial_k(ytrue=y,yhat=yhat,x=X_rm)
    gradient_b = partial_b(ytrue=y,yhat=yhat)
    k = k + (-1) * gradient_k * learning_rate
    b = b + (-1) * gradient_b * learning_rate
# 将得到的数据集和线性回归图像输出到一个图片里
plt.scatter(X_rm, y)
plt.plot(X_rm, price(X_rm, best_k, best_b), color='red')
plt.show()

下面是输出，可以看到模拟出来还是比较好的。

最小二乘法

还有一种常用的方法就是最小二乘法：
最小二乘法是一种常用的数学优化技术，它通过最小化误差的平方和来求取目标函数的最优值。
根据上面的损失函数可以发现，在损失函数取最小值时，关于k和b的偏导值一定为0，至于为什么这涉及到高数的知识，我就不具体阐述了，通过对k和b分别求偏导，并令其结果为0，求解方程组可以得到y^-=k*x^-+b^ ，其中y^-表示y的平均值，b^表示参数的估计值。在最小二乘法来看，房价是房间数的线性函数
需要注意的是，最小二乘法通过对已知数据的计算，一步就得到线性回归的参数，给人的感觉是没有经过什么学习，但是需要看到的是，其中的计算也是用数学知识得到的，任然属于机器学习范畴，只不过大多数的工作我们已经帮计算机完成了。

后记

花了好几天总算是把这篇博文写完了，算是大概搞懂了这其中的意思，我滴妈，没有好一点的数学功底和知识学起来是真滴困难，我花了好久都没搞懂那个偏导的意思（留下了悔恨的泪水），最后算是搞懂了，还是有点成就感的，也算是开启了我的秃头生涯。