滤波算法知识点汇总

作者 | 沙悟净
编辑 | 3D视觉开发者社区
✨如果觉得文章内容不错，别忘了三连支持下哦~

一、平均值滤波算法

1、算法介绍

平均值滤波算法是比较常用，也比较简单的滤波算法。在滤波时，将N个周期的采样值计算平均值，算法非常简单。当N取值较大时，滤波后的信号比较平滑，但是灵敏度差；相反N取值较小时，滤波平滑效果差，但灵敏度好。
优点：算法简单，对周期性干扰有良好的抑制作用，平滑度高，适用于高频振动的系统。
缺点：对异常信号的抑制作用差，无法消除脉冲干扰的影响。

2、实现代码

下面的代码是平均值滤波的示例代码。

float data[10];

float averageFilter(float in_data)
{
    float sum = 0;
    for(int i=0; i<9; i++)
    {
        data[i]=data[i+1];
        sum = sum + data[i];
    }
    data[9] = in_data;
    sum = sum + data[9];

    return(sum/10);

}

在代码中，data[]为全局变量，它用来记录10个周期的采样值。

averageFilter()为滤波函数，它的输入为新采集到的数据。

函数中，首先将data[]中的数据进行移位，并将新采集到的数据保存到data[]中，同时计算data[]中10个数据的和，最后返回10个数据和的平均值。

在代码中，data[]为全局变量，它用来记录10个周期的采样值。

averageFilter()为滤波函数，它的输入为新采集到的数据。

函数中，首先将data[]中的数据进行移位，并将新采集到的数据保存到data[]中，同时计算data[]中10个数据的和，最后返回10个数据和的平均值。

3、示例

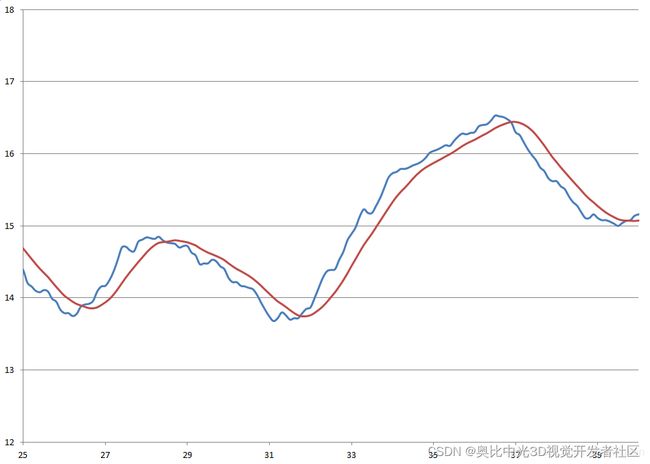
下面我们通过一个示例来体会平均值滤波的作用，滤波对象为车速信号，滤波效果如下图所示。图中，横轴为时间，单位：秒，纵轴为速度，单位km/h。

其中，蓝色为滤波前的数据，红色为滤波后的数据。可见，平均值滤波对数据进行了很大程度的平滑，但是，数据存在滞后。

参考链接：
https://blog.csdn.net/bhniunan/article/details/104589214

二、中位值滤波算法

1、算法介绍

中位值滤波算法的实现方法是采集N个周期的数据，去掉N个周期数据中的最大值和最小值，取剩下的数据的平均值。中位值滤波算法特别适用于会偶然出现异常值的系统。

中位值滤波算法应用比较广泛，比如用于一些比赛的评分，经常是去掉一个最高分去掉一个最低分，将其他评分取平均值作为选手的最终得分。

优点：相比于平均值滤波算法，中位值滤波算法能够有效滤除偶然的脉冲干扰。

缺点：与平均值滤波算法相同，中位值滤波算法也存在反应速度慢、滞后的问题。

2、实现代码

下面的代码是中位值滤波的示例代码。

float data[10];

float middleFilter(float in_data)
{
    float sum = 0;
    float temp[10];
    float change;
    int i,j;
    //记录数据
    for(i=0; i<9; i++)
    {
        data[i]=data[i+1];
    }
    data[9] = in_data;
    //复制数据
    for(i=0; i<10; i++)
        temp[i] = data[i];
    //冒泡法排序
    for(i=1; i<10; i++)
        for(j=0; j<10-i; j++)
        {
            if(temp[i] > temp[i+1])
            {
                change = temp[i];
                temp[i] = temp[i+1];
                temp[i+1] = change;
            }
        }
    //求和
    for(i=1; i<9; i++)
        sum = sum + temp[i];
    //返回平均值
    return(sum/8);

}

在上面的代码中，分为几个步骤：

步骤1：读取新数据，并更新数据数组；

步骤2：复制数据到临时数组，以便保持原始数据的顺序不变；

步骤3：对临时数组进行排序；

步骤4：计算中位平均值。

3、示例

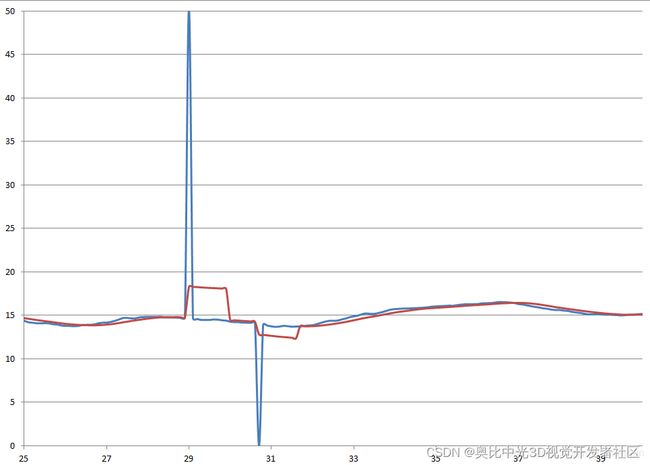
下面我们通过一个示例来体会中位值滤波的作用，滤波对象为车速信号，滤波效果如下图所示。

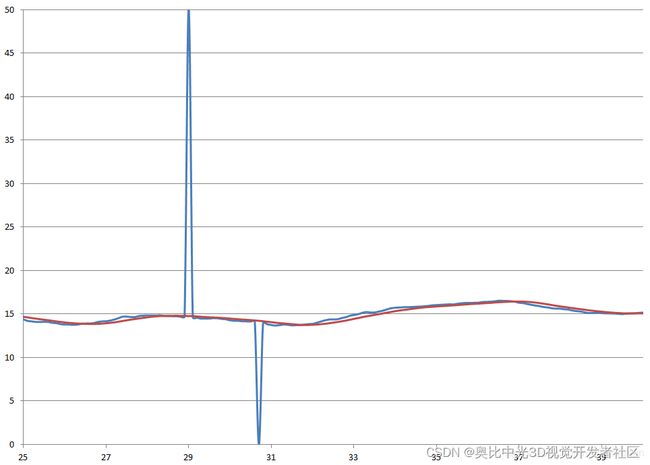
图中，横轴为时间，单位：秒，纵轴为速度，单位km/h。其中，蓝色为滤波前的数据，红色为滤波后的数据。

由图中可以看出，原始数据存在两个异常值，可能是采集过程的数据干扰或数据处理时的异常等原因造成的。

采用中位值滤波算法可以有效滤波这种异常值造成的影响。

相对于中位值滤波算法，平均值滤波算法则无法解决这个问题。如下图所示，为采用平均值滤波算法对相同的原始数据进行处理的效果，可以看到平均值滤波无法滤波异常值，而且异常值影响的时间比较长。

参考链接：
https://blog.csdn.net/bhniunan/article/details/104591123

三、 一阶滤波算法

1、算法介绍

一阶滤波算法是比较常用的滤波算法，它的滤波结果=a本次采样值+（1-a）上次滤波结果，其中，a为0~1之间的数。

一阶滤波相当于是将新的采样值与上次的滤波结果计算一个加权平均值。

a的取值决定了算法的灵敏度，a越大，新采集的值占的权重越大，算法越灵敏，但平顺性差；相反，a越小，新采集的值占的权重越小，灵敏度差，但平顺性好。

优点：对周期干扰有良好的抑制作用，适用于波动频率比较高的场合，它不用记录历史数据。

缺点：滞后、灵敏度低。

2、实现代码

下面的代码是一阶滤波的示例代码。

float final=0;
float a=0.25;

float firstOrderFilter(float in_data)
{
    final = a*in_data + (1-a)*final;    
    return(final);
}

3、示例

下面我们通过一个示例来体会一阶滤波的作用，滤波对象为车速信号，滤波效果如下图所示。

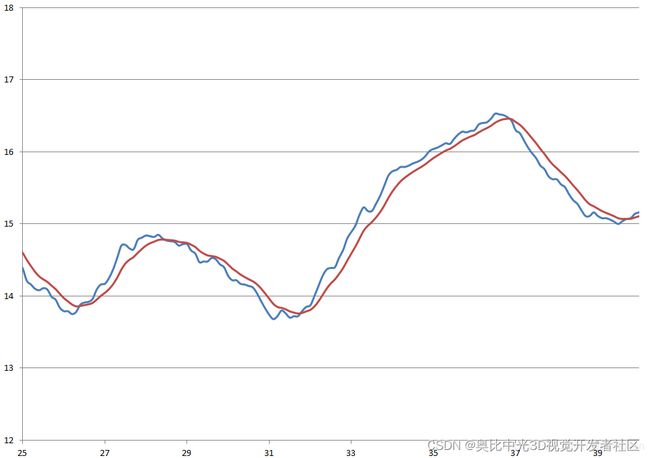
图中，横轴为时间，单位：秒，纵轴为速度，单位km/h。其中，蓝色为滤波前的数据，红色为滤波后的数据。

由图中可以看出，滤波算法使原始信号变得平滑，但是带来了滞后。

原文链接：
https://blog.csdn.net/bhniunan/article/details/104592806

四、卡尔曼滤波算法

一、算法介绍

卡尔曼滤波是一个神奇的滤波算法，应用非常广泛，它是一种结合先验经验、测量更新的状态估计算法。

1、状态估计
首先，对于一个我们关心的物理量，我们假设它符合下面的规律

其中，为该物理量本周期的实际值，为该物理量上一个周期的实际值，当然这个物理量可能不符合这个规律，我们只是做了一个假设。不同的物理量符合的规律不同，是我们的经验，我们根据这个规律可以预测我们关心的物理量。比如，我们关心的物理量是车速，如果车辆接近匀速运动时，则的取值为1，也就是这个周期与上个周期的速度相同。

下面我们再来看一下这个物理量的测量公式

其中，是这个物理量的测量值，是测量噪声。我们对一个物理进行预测，测量是一个必不可少的手段，虽然测量的不一定准，但是在很大程度上体现了物理量的实际值。这个公式体现的就是实际值与测量值的关系。还是以车速为例，是通过车速传感器得到的测量值。

实际中，物理量一般不会像我们上面的公式那样简单，一般我们用下面的公式来表示

其中，bu{k} 代表了处理噪声，这个噪声是处理模型与实际情况的差异，比如车速，他会受到人为加速、减速、路面不平等外界因素的影响。

卡尔曼滤波的基本思想是综合利用上一次的状态和测量值来对物理量的状态进行预测估计。我们用\hat{x{k}}来表示x_{k}的估计值，则有下面的公式

在这个公式中，综合利用了上一个周期的估计值和这个周期的测量值来对进行估计。其中，叫做卡尔曼增益，这个公式与一阶滤波很相似，只不过卡尔曼增益是会变的，每个周期都会更新，一阶滤波的系数则是固定值。

考虑极端的情况来分析增益的作用，当时，增益为0，这时，这表示我们这个周期的估计值与上个周期是相同的，不信任当前的测量值；当时，增益为1，这时，这表示我们这个周期的估计值与测量值是相同的，不信任上个周期的估计值，在实际应用时，介于0~1之间，它代表了对测量值的信任程度。

2、卡尔曼增益
上面我们通过卡尔曼增益来估计物理量的值，那卡尔曼增益又是如何取值的呢？我们通过下面两个公式来计算并在每个周期进行迭代更新。

在上述公式中，是测量噪声的平均值，测量噪声是符合高斯分布的，一般可以从传感器厂商那里获得测量噪声的均值，如果无法获得可以根据采集到的数据给出一个经验值。的大小对最终滤波效果的影响是比较大的。

为本周期的预测误差。我们采用分析卡尔曼增益的方法来分析预测误差的作用，即采用假设极端情况的方法。假设前一次的预测误差，根据第一个公式则，根据上面的分析，这种情况估计值为上个周期的估计值；如果前一次的预测误差，则增益变为，一般取值很小，所以，这种情况以新测量的值作为估计值。

对于第二个公式，当卡尔曼增益为0时，即采用上一个周期的预测误差；当增益为1时。

3、完整卡尔曼滤波算法
有了上面的推导，我们在下面列出来完成卡尔曼滤波的公式，卡尔曼滤波分为预测过程和更新过程两个过程，在公式中，我们又引入了缩放系数h，和协方差q。

预测过程：

更新过程：

上面的公式适合一维变量的卡尔曼滤波，将变量扩展到多维，用向量和矩阵替换上面的变量，就可以实现多维变量的卡尔曼滤波，下面的公式适用于多维变量。

预测过程：

更新过程：

二、实现代码

下面我们通过c++代码来实现卡尔曼滤波算法，所实现的算法为一维滤波算法。首先定义卡尔曼滤波的参数

typedef struct{
    float filterValue;//滤波后的值
    float kalmanGain;//Kalamn增益
    float A;//状态矩阵
    float H;//观测矩阵
    float Q;//状态矩阵的方差
    float R;//观测矩阵的方差
    float P;//预测误差
    float B;
    float u;
}KalmanInfo;

下面是卡尔曼滤波器的初始化函数，在这个函数中，info为卡尔曼滤波参数的指针。初始化的参数是针对一个车速滤波过程的设置。

void Kalm::initKalmanFilter(KalmanInfo *info)
{
    info->A = 1;
    info->H = 1;
    info->P = 0.1;
    info->Q = 0.05;
    info->R = 0.1;
    info->B = 0.1;
    info->u = 0;
    info->filterValue = 0;
}

卡尔曼滤波过程函数，函数的输入info为卡尔曼滤波参数的指针，new_value为新的测量值，函数返回滤波后的估计值。

float Kalm::kalmanFilterFun(KalmanInfo *info, float new_value)
{
    float predictValue = info->A*info->filterValue+info->B*info->u;//计算预测值
    info->P = info->A*info->A*info->P + info->Q;//求协方差
    info->kalmanGain = info->P * info->H /(info->P * info->H * info->H + info->R);//计算卡尔曼增益
    info->filterValue = predictValue + (new_value - predictValue)*info->kalmanGain;//计算输出的值
    info->P = (1 - info->kalmanGain* info->H)*info->P;//更新协方差
    return info->filterValue;
}

三、示例

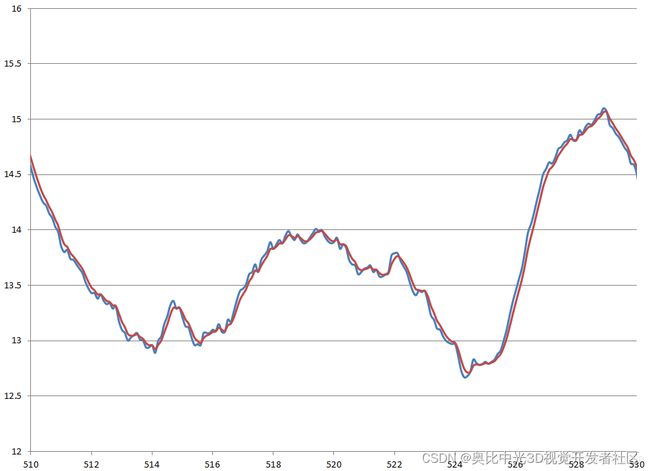
下面我们通过是一个车速滤波的示例来体验卡尔曼滤波的效果。通过上面的介绍，R对滤波效果的影响比较大，在这个示例中，我们分别将R取为0.1和0.5，来看一下车速的滤波效果。

首先，R取为0.1时，滤波效果如下图所示。其中，蓝色线为滤波前的车速，红色线为滤波后的车速。从图中可以看到滤波后的信号与滤波前的信号跟随很好，滞后很小。基本波动被滤掉了，但也带入了一些波动。

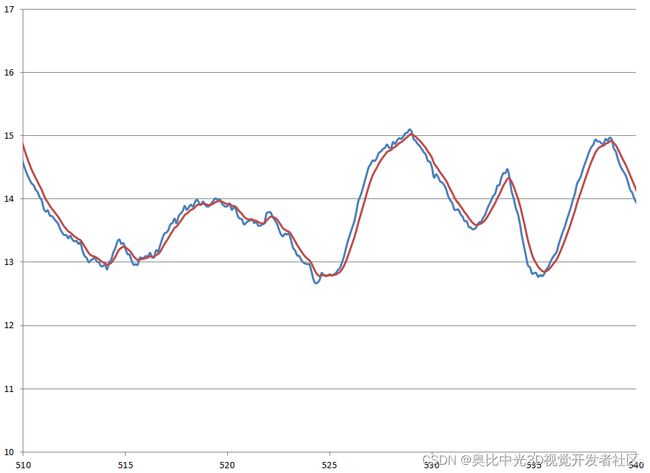
下图为R取为0.5时的滤波效果，很明显，这张图信号的跟随效果比上图要差，滞后也多，但是滤波后曲线更平滑。

原文链接：
https://blog.csdn.net/bhniunan/article/details/104607668

图像滤波算法总结

该篇主要是对图像滤波算法一个整理，主要参考的大神博客：
https://blog.csdn.net/qq_15606489/article/details/52755444

1：图像滤波
既可以在实域进行，也可以在频域进行。

图像滤波可以更改或者增强图像。通过滤波，可以强调一些特征或者去除图像中一些不需要的部分。滤波是一个邻域操作算子，利用给定像素周围的像素的值决定此像素的最终的输出值。

图像滤波可以通过公式

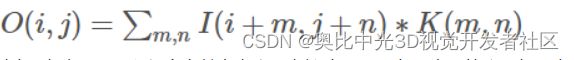
其中，K为滤波器，在很多文献中也称之为核（kernel）。常见的应用包括去噪、图像增强、检测边缘、检测角点、模板匹配等。

2：均值滤波
用其像素点周围像素的平均值代替元像素值，在滤除噪声的同时也会滤掉图像的边缘信息。在OpenCV中，可以使用boxFilter和blur函数进行均值滤波。均值滤波的核为：

3：中值滤波
中值滤波用测试像素周围邻域像素集中的中值代替原像素。中值滤波去除椒盐噪声和斑块噪声时，效果非常明显。在OpenCV中，可以使用函数medianBlur进行操作。

4：高斯滤波
这里参考一位大神的博客写的很细很好明白：https://blog.csdn.net/nima1994/article/details/79776802

总结一下：
像均值滤波，是简单的取平均值，模板系数都是1。而图像上的像素实际上是坐标离散但是值却连续的，因为越靠近的点关系越密切，越远离的点关系越疏远。因此，加权平均更合理，距离越近的点权重越大，距离越远的点权重越小。

既然是依据距离来加权平均，那么很容易想到高斯函数
如图所示：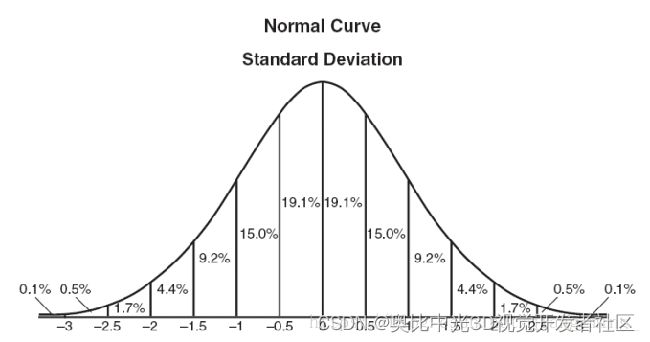

从高斯函数来看，离原点距离越近，得到的权重越高，越远离原点，得到的权重越小。

上边是一维的高斯函数，当中心点为原地时，x的均值μ=0，此时

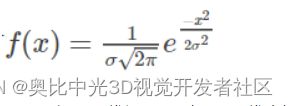
由于图像是二维矩阵，则采用二维高斯函数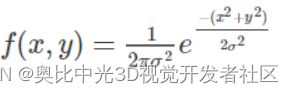
有了这个函数就可以计算滤波模板中每个点的权重了。

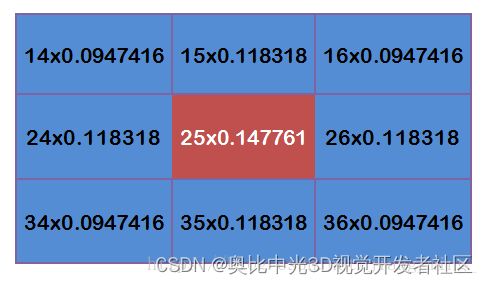
权重矩阵：
假定中心点是（0，0），那么距离它最近的8个点的坐标如下：

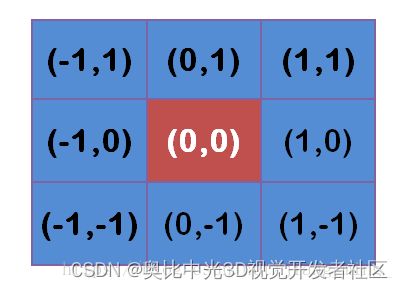
更远的点以此类推。

将这模板中的坐标x,y代入到二维高斯函数中，假定μ=0，σ为1.5,则模糊半径为1的权重矩阵如下:

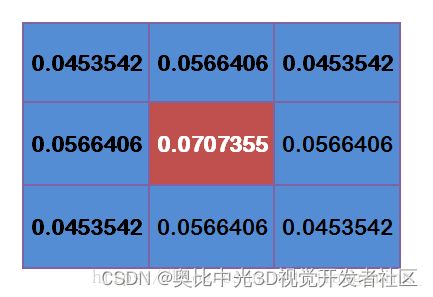
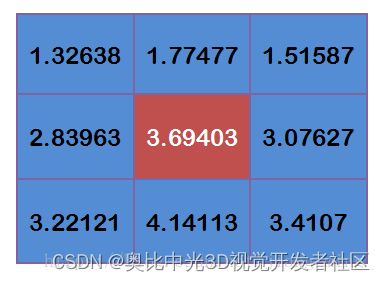
这9个点的权重总和等于0.4787147，如果只计算这9个点的加权平均，还必须让它们的权重之和等于1，因此上面9个值还要分别除以0.4787147，得到最终的权重矩阵。

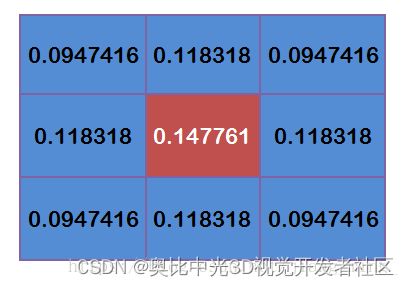
计算高斯滤波的结果
假设现在3*3高斯滤波器覆盖的图像的像素灰度值为：

每个点与上边计算得到的9个权重值相乘：

得到：

将这9个值加起来，就是中心点的高斯模糊的值。
对所有点重复这个过程，就得到了高斯模糊后的图像。如果原图是彩色图片，可以对RGB三个通道分别做高斯模糊。

边界处理
如果一个点处于边界，周边没有足够的点，怎么办？
一个变通方法，就是把已有的点拷贝到另一面的对应位置，模拟出完整的矩阵。

5：双边滤波
参考了大神的博客：http://www.360doc.com/content/17/0306/14/28838452_634420847.shtml

高斯滤波只考虑了周边点与中心点的空间距离来计算得到权重。

首先，对于图像滤波来说，一个通常的intuition是：（自然）图像在空间中变化缓慢，因此相邻的像素点会更相近。但是这个假设在图像的边缘处变得不成立。如果在边缘处也用这种思路来进行滤波的话，即认为相邻相近，则得到的结果必然会模糊掉边缘，这是不合理的，因此考虑再利用像素点的值的大小进行补充，因为边缘两侧的点的像素值差别很大，因此会使得其加权的时候权重具有很大的差别。可以理解成先根据像素值对要用来进行滤波的邻域做一个分割或分类，再给该点所属的类别相对较高的权重，然后进行邻域加权求和，得到最终结果。

双边滤波与高斯滤波相比，对于图像的边缘信息能够更好的保留，其原理为一个与空间距离相关的高斯核函数与一个灰度距离相关的高斯函数相乘。

空间距离：

其中，(xc,yc)是中心点坐标，比如为(0,0)，(xi,yi)为当前点的坐标，σ为空间域标准差。

灰度距离：

其中，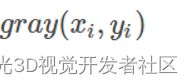
是当前像素点的灰度值，

是模板中覆盖图片区域的中心点像素的灰度值，也就是(0,0)处的灰度值，σ为值域标准差。

对于高斯滤波，仅用空间距离的权值系数核与图像卷积后确定中心点的灰度值。即认为离中心点越近，其权值系数越大。

双边滤波中加入了对灰度信息的权重，即在领域内，灰度值越接近中心点灰度值的点的权值更大，灰度值相差大的点权重越小。其权重大小则由值域高斯函数确定。

两者权重系数相乘，得到最终的卷积模板，由于双边滤波需要每个中心点领域的灰度信息来确定其系数，所以速度比一般的滤波慢得多，而且计算量增长速度为核的大小的平方。

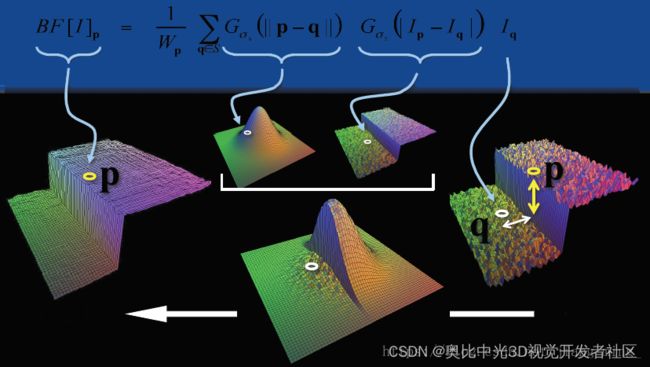
参数的选择：空间域σ的选取，和值域σ的选取。
结论：σ越大，边缘越模糊；σ越小，边缘越清晰。

版权声明：本文为奥比中光3D视觉开发者社区特约作者授权原创发布，未经授权不得转载，本文仅做学术分享，版权归原作者所有，若涉及侵权内容请联系删文

3D视觉开发者社区是由奥比中光给所有开发者打造的分享与交流平台，旨在将3D视觉技术开放给开发者。平台为开发者提供3D视觉领域免费课程、奥比中光独家资源与专业技术支持。

点击加入3D视觉开发者社区，和开发者们一起讨论分享吧~
也可移步微信关注官方公众号：3D视觉开发者社区 ，获取更多干货知识哦~