R语言实战:个人贷款违约预测模型
作者:花花_Angel
R语言爱好者,R语言中文社区原创作者
一、项目背景
本项目使用R语言对银行的个人金融业务数据进行分析,以对个人贷款是否违约进行预测。帮助业务部门及时发现问题,以避免损失。
二、数据说明
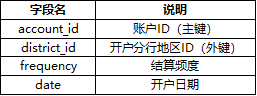
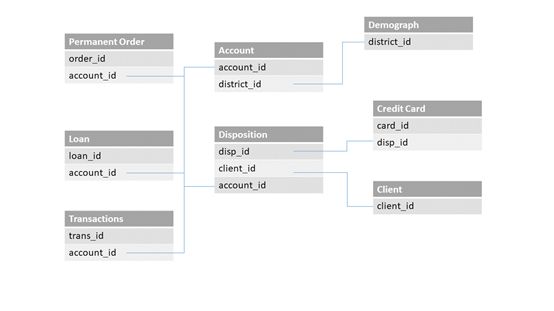
本项目数据集来自《数据科学实战:Python篇》。数据集包含8个表:账户表accounts、信用卡表card、客户信息表clients、权限分配表disp、人口地区统计表district、贷款表loans、支付订单表order、交易表trans。此数据集数据较为丰富,通过分析这份数据可以获取与银行服务相关的业务知识。
账户表(Accounts):4500条记录
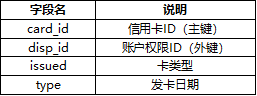
信用卡表(card):892条记录
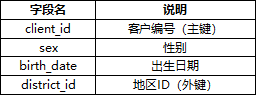
顾客信息表(clients):5369条记录
权限分配表(Disp):5369条记录
地区表(district):77条记录
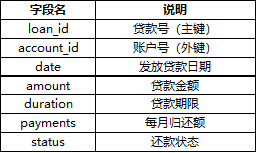
贷款表(loans):682条记录
订单表(order):6471条记录
交易表(trans):1056320条记录
各表间关系详见关系实体图(E-R图):
三、数据处理
该项目问题是典型的二分类问题,被解释变量为二分类变量,因此选择分类模型中最常使用的算法逻辑回归构建模型。
用贷款(Loans)表中的还款状态(status)变量构建被解释变量(目标变量),还款状态(status)变量记录了客户的贷款偿还情况,其中A代表合同终止且正常还款,B代表合同终止但是未还款,C代表合同未结束且正常还款,D代表合同未结束但是已经拖欠贷款了。出现贷款拖欠则用1标识,如果始终没有出现违约,则设置为0。
#数据导入
loans<-read.csv("E:\\存档\\数据科学实战:Python篇\\案例\\loans.csv",header=TRUE,stringsAsFactors=F)
accounts<-read.csv("E:\\存档\\数据科学实战:Python篇\\案例\\accounts.csv",header=TRUE)
card<-read.csv("E:\\存档\\数据科学实战:Python篇\\案例\\card.csv",header=TRUE,stringsAsFactors=F)
clients<-read.csv("E:\\存档\\数据科学实战:Python篇\\案例\\clients.csv",header=TRUE,stringsAsFactors=F)
disp<-read.csv("E:\\存档\\数据科学实战:Python篇\\案例\\disp.csv",header=TRUE,stringsAsFactors=F)
district<-read.csv("E:\\存档\\数据科学实战:Python篇\\案例\\district.csv",header=TRUE,stringsAsFactors=F)
trans<-read.csv("E:\\存档\\数据科学实战:Python篇\\案例\\trans.csv",header=TRUE,stringsAsFactors=F)
order<-read.csv("E:\\存档\\数据科学实战:Python篇\\案例\\order.csv",header=TRUE,stringsAsFactors=F)
#数据处理
#数据类型转换
accounts$date<-as.Date(accounts$date)
card$issued<-as.Date(card$issued)
card$type<-as.factor(card$type)
clients$sex<-as.factor(clients$sex)
clients$birth_date<-as.Date(clients$birth_date)
disp$type<-as.factor(disp$type)
loans$date<-as.Date(loans$date)
loans$status<-as.factor(loans$status)
trans$date<-as.Date(trans$date)
#去除千分位和美元符号,然后转换成数值类型
library(stringr)
trans$amount<-gsub(",","",trans$amount)
trans$balance<-gsub(",","",trans$balance)
trans$amount<-as.numeric(str_sub(trans$amount,2,nchar(trans$amount)))
trans$balance<-as.numeric(str_sub(trans$balance,2,nchar(trans$balance)))
#构建被解释变量
head(loans)
str(loans)
loans$New_status[loans$status=='A']<-'0'
loans$New_status[loans$status=='B']<-'1'
loans$New_status[loans$status=='C']<-'2'
loans$New_status[loans$status=='D']<-'1'
loans$New_status<-as.factor(loans$New_status)贷款表(Loans)是该项目问题的核心数据表,每个贷款帐户只有一条记录,故将所有维度的信息归结到贷款表(LOANS)上。首先提取的自变量是客户基本信息:性别、年龄等。客户的人口信息保存在客户信息表(ClIENTS)中,但是该表是以客户为主键的,需要和权限分配表(DISP)相连接才可以获得账号级别的信息。然后提取借款人居住地情况,需要连接地区表(district)。第三步提取行为信息:账户平均余额、余额的标准差、变异系数、平均入账和平均支出的比例、贷存比等。
#构建自变量
#只有“所有者”才有权限进行贷款
data<-merge(loans,disp,by.x="account_id",by.y="account_id",all.x=TRUE)
data<-data[data$type=="所有者",]
data<-merge(data,clients,by.x="client_id",by.y="client_id",all.x=TRUE)
data<-merge(data,district,by.x="district_id",by.y="A1",all.x=TRUE)
head(data)
str(data)
#求交集
data_temp<-merge(loans,trans,by.x="account_id",by.y="account_id",all=FALSE)
str(data_temp)
#一年为窗口期来取交易行为数据,即保留贷款日期前365天至贷款前1天内的交易数据
data_temp<-data_temp[data_temp$date.x>data_temp$date.y&data_temp$date.x四、构建逻辑回归模型
1)提取状态为C的用于预测。其它样本随机抽样,建立训练集与测试集
#逻辑回归
#提取状态为C的用于预测。其它样本随机抽样,建立训练集与测试集
data2<-data1[,c(6,7,10,15,16,17,18,19,20,21,22,23,24,25,26,28,30,31,32,33)]
data_model<-data2[data2$New_status!=2,]
for_predict<-data2[data2$New_status==2,]
n<-nrow(data_model)
rnd<-sample(n,n*.70)
train<-data_model[rnd,]
test<-data_model[-rnd,]2)逻辑回归建模
#使用向前逐步法进行逻辑回归建模
formula<-New_status~GDP+A4+A10+A11+A12+amount+duration+A13+A14+A15+a16+mean+sd+cv+income+out+r_out_in+r_lb+r_lincome
model<-glm(formula,data=train,family = binomial(link=logit))
forward_model<-step(model,direction="forward")
summary(forward_model)
#向后法
backward_model<-step(model,direction="backward")
summary(backward_model)
#逐步回归
both_model<-step(model,direction="both")
summary(both_model)尝试使用向前法、向后法、逐步回归三种方法进行逻辑回归,部分结果如下:
> forward_model<-step(model,direction="forward")
Start: AIC=155.4
New_status ~ GDP + A4 + A10 + A11 + A12 + amount + duration +
A13 + A14 + A15 + a16 + mean + sd + cv + income + out + r_out_in +
r_lb + r_lincome
> summary(forward_model)
Call:
glm(formula = New_status ~ GDP + A4 + A10 + A11 + A12 + amount +
duration + A13 + A14 + A15 + a16 + mean + sd + cv + income +
out + r_out_in + r_lb + r_lincome, family = binomial(link = logit),
data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.0882 -0.4193 -0.2039 0.1940 2.8449
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.548e+00 7.609e+00 0.729 0.46594
GDP -3.639e-05 4.170e-05 -0.873 0.38292
A4 9.072e-06 9.688e-06 0.936 0.34910
A10 -2.213e-02 2.285e-02 -0.968 0.33283
A11 -2.585e-04 6.516e-04 -0.397 0.69162
A12 -1.209e+00 9.801e-01 -1.233 0.21746
amount 2.860e-06 7.312e-06 0.391 0.69566
duration 6.456e-02 2.407e-02 2.682 0.00732 **
A13 7.894e-01 8.564e-01 0.922 0.35662
A14 -4.568e-02 2.487e-02 -1.837 0.06628 .
A15 -6.978e-02 2.396e-01 -0.291 0.77088
a16 1.825e-01 2.513e-01 0.726 0.46755
mean -1.850e-04 1.313e-04 -1.410 0.15866
sd 1.989e-04 2.759e-04 0.721 0.47098
cv 5.356e+00 1.039e+01 0.515 0.60632
income -4.791e-06 6.459e-06 -0.742 0.45825
out 9.703e-06 7.811e-06 1.242 0.21411
r_out_in -1.657e+00 2.653e+00 -0.624 0.53231
r_lb -5.178e-02 2.397e-01 -0.216 0.82899
r_lincome 7.186e-01 7.040e-01 1.021 0.30734
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 235.64 on 194 degrees of freedom
Residual deviance: 115.40 on 175 degrees of freedom
AIC: 155.4
Number of Fisher Scoring iterations: 7
> summary(backward_model)
Call:
glm(formula = New_status ~ A12 + duration + A14 + a16 + mean +
sd + out + r_lincome, family = binomial(link = logit), data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.9673 -0.4474 -0.2351 0.1689 2.7168
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 4.080e+00 2.880e+00 1.417 0.156561
A12 -3.257e-01 2.143e-01 -1.520 0.128574
duration 6.168e-02 1.792e-02 3.442 0.000577 ***
A14 -4.490e-02 2.131e-02 -2.107 0.035145 *
a16 5.511e-02 3.597e-02 1.532 0.125487
mean -2.357e-04 4.698e-05 -5.016 5.27e-07 ***
sd 3.473e-04 6.630e-05 5.239 1.62e-07 ***
out 3.161e-06 1.662e-06 1.902 0.057179 .
r_lincome 1.001e+00 4.895e-01 2.046 0.040764 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 235.64 on 194 degrees of freedom
Residual deviance: 119.49 on 186 degrees of freedom
AIC: 137.49
Number of Fisher Scoring iterations: 7
> summary(both_model)
Call:
glm(formula = New_status ~ A12 + duration + A14 + a16 + mean +
sd + out + r_lincome, family = binomial(link = logit), data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.9673 -0.4474 -0.2351 0.1689 2.7168
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 4.080e+00 2.880e+00 1.417 0.156561
A12 -3.257e-01 2.143e-01 -1.520 0.128574
duration 6.168e-02 1.792e-02 3.442 0.000577 ***
A14 -4.490e-02 2.131e-02 -2.107 0.035145 *
a16 5.511e-02 3.597e-02 1.532 0.125487
mean -2.357e-04 4.698e-05 -5.016 5.27e-07 ***
sd 3.473e-04 6.630e-05 5.239 1.62e-07 ***
out 3.161e-06 1.662e-06 1.902 0.057179 .
r_lincome 1.001e+00 4.895e-01 2.046 0.040764 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 235.64 on 194 degrees of freedom
Residual deviance: 119.49 on 186 degrees of freedom
AIC: 137.49
Number of Fisher Scoring iterations: 7从模型结果可知,三种方法的模型结果基本保持一致,其中申请贷款前一年的贷收比(r_lincome)、存款余额的标准差(sd)、贷款期限(duration)与违约正相关。存款余额的均值(mean)、贷款者当地1000人中有多少企业家(A14)与违约负相关。以上这些回归系数的正负号均符合预期,而且均显著。
五、模型评估
使用测试数据进行模型效果评估。此项目选取了逐步逻辑回归模型,且计算了准确率和ROC曲线下面积(AUC)。
#用测试集做模型评估
pre<-predict(both_model,test,type="response")
#在预测数据集中,概率大于0.5,违约,概率小于0.5,不违约
test$pre_New_status<-ifelse(predict(both_model,test,type="response")>0.5,1,0)
table(test$New_status,test$pre_New_status)
#准确率计算
sum_diag<-sum(diag(table(test$New_status,test$pre_New_status)))
sum<-sum(table(test$New_status,test$pre_New_status))
accuracy<-sum_diag/sum
accuracy
#ROC曲线评估
library(pROC)
library(sjmisc)
roc_curve<-roc(test$New_status~pre)
x<-1-roc_curve$specificities
y<-roc_curve$sensitivities
plot(x=x,y=y,xlim=c(0,1),ylim=c(0,1),xlab = '1-specificity',ylab = 'Sensitivity',main='ROC Curve',type='l',lwd=2.5)
abline(a=0,b=1,col='gray')
auc<-roc_curve$auc
text(0.5,0.4,paste('AUC:',round(auc,digits = 2)),col='blue')可以看到模型的准确率为0.87,模型的ROC曲线非常接近左上角,其曲线下面积(AUC)为0.9,这说明模型的分类能力较强。
六、模型预测及应用
在这个项目中,贷款状态为C的帐户是尚没有出现违约的合同未到期客户。我们可以通过该模型得到每笔贷款的违约预测概率。根据概率可以知道这些贷款客户中有些人的违约可能性较高,需要业务人员重点关注。一旦发现问题时,可以及时处理,挽回损失。
#预测
for_predict$predict<-predict(both_model,for_predict,type="response")图表色彩运用原理的全面解析
R_ggplot2基础(一)
用R语言实现数据离散化
公众号后台回复关键字即可学习
回复 爬虫 爬虫三大案例实战
回复 Python 1小时破冰入门回复 数据挖掘 R语言入门及数据挖掘
回复 人工智能 三个月入门人工智能
回复 数据分析师 数据分析师成长之路
回复 机器学习 机器学习的商业应用
回复 数据科学 数据科学实战
回复 常用算法 常用数据挖掘算法