如何通过torch使用梯度下降法( Gradient descent)求函数极小值
1. 梯度下降法
梯度下降法(Gradient descent,简称GD)是一阶最优化算法,计算过程就是沿梯度下降的方向求解极小值,公式如下所示,其中 μ \mu μ表示学习率, g t g^t gt表示梯度, t t t表示第t次迭代。通过多次迭代计算上面公式可以求得极小值点(非最小值)。
x t + 1 = x t − μ ⋅ g t x^{t+1}=x^t-\mu·g^t xt+1=xt−μ⋅gt
torch.optim.SGD
在torch中内置许多算法,其中torch.optim.SGD函数就是随机梯度下降法。其参数包括:
- params (iterable)
- lr (float) – 学习率
params是需要进行优化的参数,lr就是学习率。
在使用SDG()需要用到他的两个方法:zero_grad()和step()以及参数的梯度计算:backward()
-
SDG(params, lr).zero_grad(),这个方法的作用是将params所包含的张量的梯度置0,因为每次使用backward()计算得到的梯度都会累加到原来的梯度上。 -
SDG(params, lr).step(),这个方法是执行 x t + 1 = x t − μ ⋅ g t x^{t+1}=x^t-\mu·g^t xt+1=xt−μ⋅gt这个公式,也就是更新params包含的参数的值。深入分析源码的可以考:pytorch中optimizer.zero_grad(), loss.backward(), optimizer.step()的作用及原理随机梯度下降算法是梯度下降算法中的一种,当训练数据只有一条的时候SGD和GD是一样的。具体可参考:三种梯度下降法对比(Batch gradient descent、Mini-batch gradient descent 和 stochastic gradient descent)
import torch
import matplotlib.pyplot as plt
x = torch.tensor(3., requires_grad=True)
optimizer = torch.optim.SGD([x], lr=0.15)
# 进行十次迭代
x_record, y_record = [], [] # 记录每次更新后的x和y的值
for i in range(10):
y = x**2 # 每次x都会更新,所以y也需要同时更新
x_record.append(x.item()) # x的类型是tensor,调用item()是将其转化成python基本数据类型。
y_record.append(y.item())
optimizer.zero_grad() # 每次计算梯度前都要将原来的梯度置0
y.backward() # 计算梯度
optimizer.step() # 更新x值。
# 画坐标图
a = torch.linspace(-3., 3., 1000) # 从-3到3生成1000的等距的点
b = a**2
plt.figure(figsize=(6, 4)) # 创建一张长为6,宽为4的画布
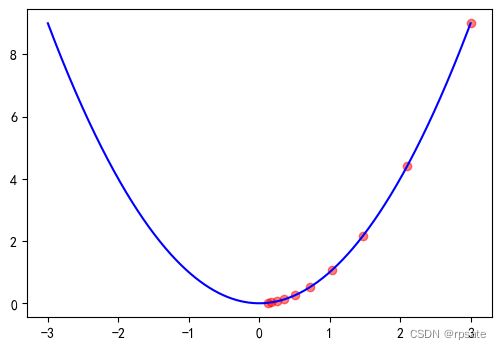
plt.plot(a, b, c='b') # 画出y=x^2的曲线
plt.scatter(x_record, y_record, c='r', alpha=0.5) # 画出x下降过程中经过的点
plt.show()
2. 动量梯度下降法
动量梯度下降法是动量梯度下降法的一种改进,是将物理学中动量概念引入梯度下降法。公式如下:
x t + 1 = x t + m t + 1 x^{t+1}=x^t+m^{t+1} xt+1=xt+mt+1 其中 m t m^t mt表示第t次迭代是的动量,关于m的公式如下(初始动量 m 0 = 0 m^0=0 m0=0):
m t + 1 = λ ⋅ m t − μ ⋅ g t m^{t+1}=\lambda·m^t-\mu·g^t mt+1=λ⋅mt−μ⋅gt
为什么要引入动量
有时候通过梯度下降法得到的值不是最优解,有可能是局部最优解,如下图一所示。引入动量的概念时,求最小值就像一个球从高处落下,落到局部最低点时会继续向前探索,有可能得到更小的值,如下图二所示。
设置
torch.optim.SGD()中的momentum参数就引入了动量系数(公式中的 λ \lambda λ)。
import torch
# 未引入动量
x1 = torch.tensor([-10.], requires_grad=True)
optimizer = torch.optim.SGD([x1], lr=0.01)
x1_list, y1_list = [], []
for i in range(10):
y1 = 16 * x1.pow(2) - x1.pow(3)
x1_list.append(x1.item())
y1_list.append(y1.item())
optimizer.zero_grad()
y1.backward()
optimizer.step()
# 引入动量
x2 = torch.tensor([-10.], requires_grad=True)
optimizer = torch.optim.SGD([x2], lr=0.01, momentum=0.76)
x2_list, y2_list = [], []
for i in range(10):
y2 = 16 * x2.pow(2) - x2.pow(3)
x2_list.append(x2.item())
y2_list.append(y2.item())
optimizer.zero_grad()
y2.backward()
optimizer.step()
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
x = torch.linspace(-10., 20., 1000)
y = 16 * x.pow(2) - x.pow(3)
plt.figure(figsize=(12, 4))
# 图一
plt.subplot(1, 2, 1)
plt.grid(True, linestyle='--', alpha=0.5)
plt.plot(x, y, c='b')
plt.scatter(x1_list, y1_list, c='r', alpha=0.5)
plt.title('图一', y=-0.2)
# 图二
plt.subplot(1, 2, 2)
plt.grid(True, linestyle='--', alpha=0.5)
plt.plot(x, y, c='b')
plt.scatter(x2_list, y2_list, c='r', alpha=0.5)
plt.title('图二', y=-0.2)
plt.show()
参考文献
pytorch中optimizer.zero_grad(), loss.backward(), optimizer.step()的作用及原理
三种梯度下降法对比(Batch gradient descent、Mini-batch gradient descent 和 stochastic gradient descent)